福建省石狮市2021年数学中考学业质量检测试试卷

试卷更新日期：2021-11-03 类型：中考模拟

进入出卷网下载

一、单选题

1. $- \frac{1}{2021}$ 的绝对值是（）

A、 $- \frac{1}{2021}$ B、-2021 C、 $\frac{1}{2021}$ D、2021

查看试题解析
2. 某城市四月初连续四天的天气情况如图所示，这四天中，温差最大的是（）

A、周一 B、周二 C、周三 D、周四

查看试题解析
3. 下列运算结果等于x⁶的是（）

A、x²•x³ B、x⁶÷x C、x²+x⁴ D、（x³）²

查看试题解析
4. 如图，点 $E$ ， $F$ 在 $A C$ 上， $∠ B = ∠ D = 90 °$ ，则下列结论正确的是（）

A、 $∠ A = ∠ C$ B、 $D E$ ∥ $B F$ C、 $A E = C F$ D、 $∠ D = ∠ A + ∠ A F B$

查看试题解析
5. 如图是一个几何体的正视图，则这个几何体可能是（）

A、 B、 C、 D、

查看试题解析
6. 两个不透明的口袋中各有三个相同的小球，将每个口袋中的小球分别标号为1，2，3.从这两个口袋中分别摸出一个小球，则下列事件为随机事件的是（）

A、两个小球的标号之和等于1 B、两个小球的标号之和等于6 C、两个小球的标号之和大于1 D、两个小球的标号之和大于6

查看试题解析
7. 在数轴上，点 $A$ ， $B$ 在原点 $O$ 的两侧，分别表示数 $a$ 和 $b$ ( $b$ ＞ $1$ )，将点 $A$ 向右平移 $1$ 个单位长度得到点 $C$ .若 $O C = O B$ ，则 $a$ ， $b$ 的关系是（）

A、 $a + b = 1$ B、 $a - b = 1$ C、 $a + b = - 1$ D、 $a - b = - 1$

查看试题解析
8. 如图， $⊙ A$ 经过平面直角坐标系的原点O ，交x轴于点B(-4，0)，交y轴于点C(0，3)，点D为第二象限内圆上一点.则∠CDO的正弦值是（）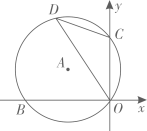

A、 $\frac{3}{5}$ B、 $- \frac{3}{4}$ C、 $\frac{3}{4}$ D、 $\frac{4}{5}$

查看试题解析
9. 已知：等腰直角三角形ABC的腰长为4，点M在斜边AB上，点P为该平面内一动点，且满足PC＝2，则PM的最小值为（）

A、2 B、2 $\sqrt{2}$ ﹣2 C、2 $\sqrt{2}$ +2 D、2 $\sqrt{2}$

查看试题解析
10. 已知点 $A$ ( $x_{1}$ ， $y_{1}$ )与点 $B$ ( $x_{2}$ ， $y_{2}$ )在二次函数 $y = - {(x - m)}^{2} - m + 1$ ( $m$ 为常数)的图象上，且 $x_{1}$ ＜ $x_{2}$ ， $x_{1} + x_{2}$ ＞ $2 m$ ，则下列判断正确的是（）

A、 $y_{1}$ ＞ $y_{2}$ B、 $y_{1} = y_{2}$ C、 $y_{1}$ ＜ $y_{2}$ D、 $y_{1}$ ≤ $y_{2}$

查看试题解析

二、填空题

11. 计算： ${(2 - \sqrt{3})}^{0} - 2^{- 1} =$ .

查看试题解析
12. 若 $m$ ＜ $\sqrt{26}$ ＜ $m + 1$ ，且 $m$ 为整数，则 $m =$ .

查看试题解析
13. 某 $5$ 人学习小组在寒假期间进行线上测试，其成绩（分）分别为： $86, 88, 90, 92, 94$ ，方差为 $s^{2} = 8.0$ ．后来老师发现每人都少加了 $2$ 分，每人补加 $2$ 分后，这 $5$ 人新成绩的方差 $s_{新}^{2} =$ ．

查看试题解析
14. 中国清代数学著作《御制数理精蕴》中有这样一道题：“马四匹、牛六头，共价四十八两（“两”是我国古代货币单位）；马三匹、牛五头，共价三十八两.则马每匹价两.

查看试题解析
15. 如图，在菱形 $A B C D$ 中， $∠ B A D = α$ ，将菱形 $A B C D$ 绕点 $A$ 逆时针旋转得到菱形 $A E F G$ ， $E F$ 与 $C D$ 交于点 $P$ .当点 $A$ ， $E$ ， $C$ 在同一条直线上时， $∠ C P E$ 的大小为.（用含 $α$ 的代数式表示）

查看试题解析
16. 如图，在平面直角坐标系中，矩形 $O A C B$ 的顶点 $A$ 的坐标为(0，4)，反比例函数 $y = \frac{12}{x}$ 的图象与边 $A C$ 交于点 $E$ ，与边 $B C$ 交于点 $F$ .若点 $C$ 关于直线 $E F$ 的对称点 $C^{'}$ 恰好在 $x$ 轴上，则点 $C^{'}$ 的坐标是.

查看试题解析

三、解答题

17. 解不等式组： ${\begin{array}{l} 3 (1 - x) + 2 < 8 \\ \frac{x + 4}{6} ⩾ 1 \end{array}$

查看试题解析
18. 先化简，再求值： $(1 - \frac{x}{x + 1}) \div \frac{x^{2} - 2 x + 1}{x^{2} - 1}$ ，其中 $x = \sqrt{3} + 1$ .

查看试题解析
19. 如图， $A C$ 是四边形 $A B C D$ 的对角线， $∠ A C D = ∠ B$ ，点 $E$ ， $F$ 分别在 $A B$ ， $B C$ 上， $B E = C D$ ， $B F = C A$ ，连接 $E F$ .

(1)、求证： $A D = E F$ ；

(2)、若 $E F$ ∥ $A C$ ， $∠ D = 78 °$ ，求 $∠ B A C$ 的度数.

查看试题解析

20. 某超市有线上和线下两种销售方式.与2019年4月份相比，该超市2020年4月份销售总额增长

10 %

，其中线上销售额增长43%，线下销售额增长4%.

(1)、设2019年4月份的销售总额为

a

元，线上销售额为

x

元，请用含

a

，

x

的代数式表示2020年4月份的线下销售额（直接在表格中填写结果）；

时间	销售总额（元）	线上销售额（元）	线下销售额（元）
2019年4月份	$a$	$x$	$a - x$
2020年4月份	$1.1 a$	$1.43 x$

(2)、求2020年4月份线上销售额与当月销售总额的比值.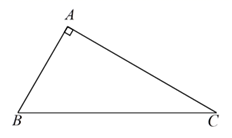

查看试题解析

21. 如图，在 $R t$ △ $A B C$ 中， $∠ A = 90 °$ ， $∠ C = 30 °$ ， $B C = 12$ .

(1)、求作：以 $∠ B$ 为一个内角的菱形 $B D E F$ ，使顶点 $E$ 在 $A C$ 边上；(要求：尺规作图，不写作法，保留作图痕迹)

(2)、求菱形 $B D E F$ 的边长.

查看试题解析
22. 如图，在平行四边形ABCD中，∠D＝60°，对角线AC⊥BC，⊙O经过点A，B，与AC交于点M，连接AO并延长与⊙O交于点F，与CB的延长线交于点E，AB＝EB．

(1)、求证：EC是⊙O的切线；

(2)、若AD＝2 $\sqrt{3}$ ，求 $\overset{⌢}{AM}$ 的长（结果保留π）．

查看试题解析

23. 某工厂承接了一批加工业务，双方约定：原材料由委托方供给，加工出来的每件产品按质量标准评定为

A

，

B

，

C

，

D

四个等级，并由委托方按委托加工数量全部收回.对于每件

A

级品、

B

级品、

C

级品，委托方分别付给加工厂加工费90元、50元、20元，对于每件

D

级品，加工厂要赔偿委托方原材料费50元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为25元/件，乙分厂加工成本费为20元/件.该厂为决定由哪个分厂承接加工业务，在两个分厂各试加工了100件这种产品，并统计了这些产品的等级，整理如下：

甲分厂产品等级的频数分布表
等级	$A$	$B$	$C$	$D$
频数	40	20	20	20
乙分厂产品等级的频数分布表
等级	$A$	$B$	$C$	$D$
频数	28	17	34	21

(1)、分别估计甲、乙两个分厂加工出来的一件产品为

A

级品的概率；

(2)、分别求甲、乙两个分厂加工出来的100件产品的平均利润.若以平均利润为依据，则该厂应选哪个分厂承接加工业务？

查看试题解析

24. 如图，已知四边形 $A B C D$ 是矩形，点 $E$ 在 $B A$ 的延长线上， $A E = A D$ ，连接 $E C$ ，交 $A D$ 于点 $F$ ，交 $B D$ 于点 $G$ ， $B D ⊥ E C$ .

(1)、求证： $A F = A B$ ；

(2)、若 $A D = 2$ ，求 $A B$ 的长；

(3)、连接 $A G$ ，求证： $E G - D G = \sqrt{2} A G$ .

查看试题解析
25. 已知二次函数 $y = - 2 x^{2} + b x + c$ （ $b$ ， $c$ 为常数）的图象经过点 $(2 ， - 1)$ ，其对称轴为直线 $x = 1$ .

(1)、求该二次函数的表达式；

(2)、点 $P (0 ， n)$ 在 $y$ 轴上，若 $n < 1$ ，过点 $P$ 作 $x$ 轴的平行线与该二次函数的图象交于 $E$ ， $F$ 两点，当 $n$ 取某一范围内的任意实数时， $| F P - E P$ $|$ 的值始终是一个定值 $d$ ，求此时 $n$ 的范围及定值 $d$ .

(3)、是否存在两个不等实数 $s ， t (s < t)$ ，当 $s \leq x \leq t$ 时，恰好有 $11 - 6 t \leq y \leq 11 - 6 s$ .若存在，求出这样的实数 $s$ ， $t$ ；若不存在，请说明理由.

查看试题解析