福建省2021年数学中考模拟试卷(六)
试卷更新日期:2021-11-03 类型:中考模拟
一、单选题
-
1. 下列实数中,无理数的是( )A、2021 B、 C、 D、2. 如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )A、
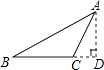 B、
B、 C、
C、 D、
D、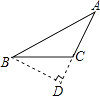 3. 我市纺织业主动调结构、转方式,产业水平提升实现了历史性的突破,2021年完成工业总产值1140亿元,成为全省少有的超千亿产业集群,1140亿用科学记数法表示为( )A、 B、 C、 D、4. 下列图形中,不是轴对称图形的是( )A、
3. 我市纺织业主动调结构、转方式,产业水平提升实现了历史性的突破,2021年完成工业总产值1140亿元,成为全省少有的超千亿产业集群,1140亿用科学记数法表示为( )A、 B、 C、 D、4. 下列图形中,不是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 在算式 □ 的□中填上运算符号,使结果最大,这个运算符号是( )A、加号 B、减号 C、乘号 D、除号6. 下列运算正确的是( )A、 B、 C、 D、7. 将△ABC平移得到△ ,若 ,则 的度数是( )A、10° B、80° C、100° D、160°8. 正六边形的边长为2,则该正六边形的边心距是( )A、 B、1 C、2 D、9. 在平面直角坐标系中,二次函数y=a(x−h)2(a≠0)的图象可能是( )A、
5. 在算式 □ 的□中填上运算符号,使结果最大,这个运算符号是( )A、加号 B、减号 C、乘号 D、除号6. 下列运算正确的是( )A、 B、 C、 D、7. 将△ABC平移得到△ ,若 ,则 的度数是( )A、10° B、80° C、100° D、160°8. 正六边形的边长为2,则该正六边形的边心距是( )A、 B、1 C、2 D、9. 在平面直角坐标系中,二次函数y=a(x−h)2(a≠0)的图象可能是( )A、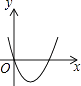 B、
B、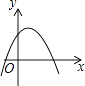 C、
C、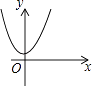 D、
D、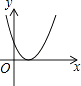 10. 将一正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去上面的小直角三角形将留下的纸片展开,得到的图形是( )
10. 将一正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去上面的小直角三角形将留下的纸片展开,得到的图形是( )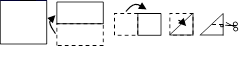 A、
A、 B、
B、 C、
C、 D、
D、 11. 在平面直角坐标系中,我们把横、纵坐标都是整数的点称为整点.若一次函数 (k为整数)与 的图象的交点是整点,则k的不同取值的个数是( )A、3 B、4 C、5 D、6
11. 在平面直角坐标系中,我们把横、纵坐标都是整数的点称为整点.若一次函数 (k为整数)与 的图象的交点是整点,则k的不同取值的个数是( )A、3 B、4 C、5 D、6二、多选题
-
12. 为了解居民节约用水的情况,增强居民的节水意识,表是某个单元的住户当月用水量的调查结果:则关于这12户居民月用水量,下列说法正确的是( )
住户(户)
2
4
5
1
月用水量(方/户)
2
4
6
10
A、中位数是6方 B、众数是6方 C、平均数是3方 D、平均数是5.5方三、填空题
-
13. 因式分解: =.14. 在一个不透明的布袋中装有2个白球和n个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球,摸到黄球的概率是 ,则 .15. 化简 的结果是.16. 点 关于直线 对称的点的坐标是.17. 如图,△ABC的三个顶点在边长为1的正方形网格的格点上,则sin =.
 18. 如图,在平面直角坐标系中,等腰直角△OAB的斜边OB在x轴上,且OB=4,反比例函数y= (x>0)的图象经过OA的中点C,交AB于点D,则点D坐标是.
18. 如图,在平面直角坐标系中,等腰直角△OAB的斜边OB在x轴上,且OB=4,反比例函数y= (x>0)的图象经过OA的中点C,交AB于点D,则点D坐标是.
四、解答题
-
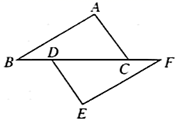
19. 计算:20. 化简:21. 如图,点 , 在 上, , , .求证: .
 22. 七一商场以150元/台的价格购进某款电风扇若干台,很快售完.商场用相同的货款再次购进这款电风扇,因价格提高30元,进货量减少了10台.这两次各购进电风扇多少台?23. 2011年5月,我市某中学举行了“中国梦•校园好少年”演讲比赛活动,根据学生的成绩划分为A,B,C,D四个等级,并绘制了不完整的两种统计图.
22. 七一商场以150元/台的价格购进某款电风扇若干台,很快售完.商场用相同的货款再次购进这款电风扇,因价格提高30元,进货量减少了10台.这两次各购进电风扇多少台?23. 2011年5月,我市某中学举行了“中国梦•校园好少年”演讲比赛活动,根据学生的成绩划分为A,B,C,D四个等级,并绘制了不完整的两种统计图.
根据图中提供的信息,回答下列问题:
(1)、参加演讲比赛的学生共有 ▲ 人,并把条形图补充完整;(2)、扇形统计图中,m= , n=;C等级对应扇形的圆心角为度;(3)、学校欲从获A等级的学生中随机选取2人,参加市举办的演讲比赛,请利用列表法或树状图法,求获A等级的小明参加市比赛的概率.24. 如图, 中, ,AD⊥BC,垂足为D.求作:∠ABC的平分线,分别交AD,AC于P,Q两点,并证明 是等腰三角形.
(要求:尺规作图,保留作图痕迹,不写作法)
 25. 如图,AB是⊙O的直径,点P是⊙O 外一点,PA切⊙O于点A,连接OP,过点B作BC OP交⊙O于点C,点E是 的中点.
25. 如图,AB是⊙O的直径,点P是⊙O 外一点,PA切⊙O于点A,连接OP,过点B作BC OP交⊙O于点C,点E是 的中点. (1)、求证:PC是⊙O的切线;(2)、若 ,求CE的长.26. 如图1,在边长为3的等边△ABC中,过点A作AC的垂线交CB延长线于点D.点P,Q分别在线段BD,AC上,且 .设 .
(1)、求证:PC是⊙O的切线;(2)、若 ,求CE的长.26. 如图1,在边长为3的等边△ABC中,过点A作AC的垂线交CB延长线于点D.点P,Q分别在线段BD,AC上,且 .设 . (1)、求BD的长;(2)、过点Q作QH⊥BC,垂足为H,当以P,Q,H为顶点的三角形与△CDA相似时,求x的值;(3)、如图2,PQ交AB于点E,过点E作EF BD交AD于点F.设 ,求m与x之间的函数关系式.27. 在平面直角坐标系中,抛物线 与直线 交于A,B两点,点A在点B的左侧.
(1)、求BD的长;(2)、过点Q作QH⊥BC,垂足为H,当以P,Q,H为顶点的三角形与△CDA相似时,求x的值;(3)、如图2,PQ交AB于点E,过点E作EF BD交AD于点F.设 ,求m与x之间的函数关系式.27. 在平面直角坐标系中,抛物线 与直线 交于A,B两点,点A在点B的左侧. (1)、如图1,当 时,直接写出A,B两点的坐标;(2)、在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;(3)、如图2,抛物线 与 x 轴交于C,D两点(点C在点D的左侧).当以 为直径的⊙E与直线 相切于点Q时,请求出此时 的值.
(1)、如图1,当 时,直接写出A,B两点的坐标;(2)、在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;(3)、如图2,抛物线 与 x 轴交于C,D两点(点C在点D的左侧).当以 为直径的⊙E与直线 相切于点Q时,请求出此时 的值.
-