初中数学苏科版九年级上学期期中复习专题5 圆的内接多边形
试卷更新日期:2021-11-03 类型:复习试卷
一、单选题
-
1. 下列命题正确的是( )A、正三角形的内切圆的半径与外接圆半径之比为2﹕1 B、正六边形的边长等于其外接圆的半径 C、圆的外切正多边形的边长等于其边心距的倍 D、各边相等的圆的外切四边形是正方形2. 若三角形的外心在这个三角形的一边上,则这个三角形是( ).A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定3. 对于三角形的外心,下列说法错误的是( )A、它到三角形三个顶点的距离相等 B、它是三角形外接圆的圆心 C、它是三角形三条边垂直平分线的交点 D、它一定在三角形的外部4. 根据圆规作图的痕迹,可用直尺成功找到三角形外心的是( )A、
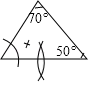 B、
B、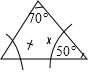 C、
C、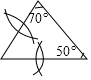 D、
D、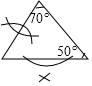 5. 钝角三角形的外心在( )
5. 钝角三角形的外心在( )
A、三角形的内部 B、三角形的外部 C、三角形的钝角所对的边上 D、以上都有可能6. 如图,四边形ABCD内接于⊙O,若∠A=40°,则∠C=( )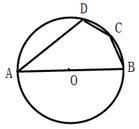 A、110° B、120° C、135° D、140°7. 如图,四边形 是 的内接四边形, ,则 的度数为( )
A、110° B、120° C、135° D、140°7. 如图,四边形 是 的内接四边形, ,则 的度数为( ) A、70° B、90° C、100° D、110°8. 如图,四边形 内接于 .若 ,则 的大小为( )
A、70° B、90° C、100° D、110°8. 如图,四边形 内接于 .若 ,则 的大小为( )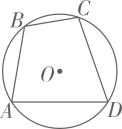 A、 B、 C、 D、9. 如图,四边形ABCD为⊙O的内接四边形,E是BC延长线上的一点,已知∠BOD=100°,则∠DCE的度数为( )
A、 B、 C、 D、9. 如图,四边形ABCD为⊙O的内接四边形,E是BC延长线上的一点,已知∠BOD=100°,则∠DCE的度数为( )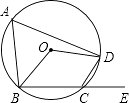 A、40° B、60° C、50° D、80°10. 若正六边形的边长为6,则其外接圆半径为( )A、3 B、3 C、3 D、611. 如图,正六边形ABCDEF内接于⊙O,点P是 上的任意一点,则∠APB的大小是( )
A、40° B、60° C、50° D、80°10. 若正六边形的边长为6,则其外接圆半径为( )A、3 B、3 C、3 D、611. 如图,正六边形ABCDEF内接于⊙O,点P是 上的任意一点,则∠APB的大小是( )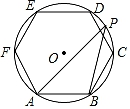 A、15° B、30° C、45° D、60°12. ⊙O的半径为2,则它的内接正六边形的边长为( )A、2 B、2
A、15° B、30° C、45° D、60°12. ⊙O的半径为2,则它的内接正六边形的边长为( )A、2 B、2 C、
C、  D、2
D、2  13. 如图,⊙O是正五边形ABCDE的外接圆,则正五边形的中心角∠AOB的度数是( )
13. 如图,⊙O是正五边形ABCDE的外接圆,则正五边形的中心角∠AOB的度数是( ) A、72° B、60° C、54° D、36°
A、72° B、60° C、54° D、36°二、填空题
-
14. 已知△ABC的三边长分别是6,8,10,则△ABC外接圆的直径是 .
15. 如图,△ABC是⊙O的内接正三角形,⊙O的半径为3,则图中阴影部分的面积是 .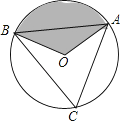 16. 如图,在圆内接四边形ABCD中,若∠A,∠B,∠C的度数之比为4:3:5,则∠D的度数是°.
16. 如图,在圆内接四边形ABCD中,若∠A,∠B,∠C的度数之比为4:3:5,则∠D的度数是°.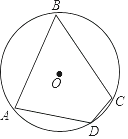 17. 如图,⊙O的内接四边形ABCD中,∠A=110°,则∠BOD等于°.
17. 如图,⊙O的内接四边形ABCD中,∠A=110°,则∠BOD等于°. 18. 如图,▱BCDE的顶点B、C、D在半圆O上,顶点E在直径AB上,连接AD,若∠CDE=68°,则∠ADE的度数为°.
18. 如图,▱BCDE的顶点B、C、D在半圆O上,顶点E在直径AB上,连接AD,若∠CDE=68°,则∠ADE的度数为°.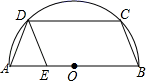 19. 正方形ABCD是半径为10的圆内接正方形,则正方形的周长为 .20. 已知正六边形的边长为2,则它的内切圆的半径为 .21. 如图,AB,AC分别为⊙O的内接正六边形,内接正方形的一边,BC是圆内接n边形的一边,则n等于.
19. 正方形ABCD是半径为10的圆内接正方形,则正方形的周长为 .20. 已知正六边形的边长为2,则它的内切圆的半径为 .21. 如图,AB,AC分别为⊙O的内接正六边形,内接正方形的一边,BC是圆内接n边形的一边,则n等于.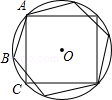 22. 如图,正五边形 内接于 ,若 的半径为 ,则弧 的长为.
22. 如图,正五边形 内接于 ,若 的半径为 ,则弧 的长为.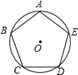 23. 如图,⊙O是正五边形ABCDE的外接圆,则∠CAD=°.
23. 如图,⊙O是正五边形ABCDE的外接圆,则∠CAD=°.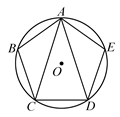
三、解答题
-
24. 如图,在圆内接四边形ABCD中,O为圆心,∠BOD=160°,求∠BCD的度数.
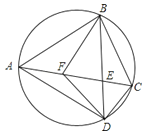
 25. 如图,已知四边形ABCD内接于圆,对角线AC与BD相交于点E,F在AC上,AB=AD,∠BFC=∠BAD=2∠DFC.
25. 如图,已知四边形ABCD内接于圆,对角线AC与BD相交于点E,F在AC上,AB=AD,∠BFC=∠BAD=2∠DFC.(1)若∠DFC=40°,求∠CBF的度数;
(2)求证:CD⊥DF.
四、综合题
-
26. 如图,10-1、10-2、10-3、…、10-n分别是⊙O的内接正三角形ABC,正四边形ABCD,正五边形ABCDE,、…、正n边形ABCD…,点M、N分别从点B,C开始以相同的速度在⊙O上逆时针运动
 (1)、求图10-1中∠APN的度数;
(1)、求图10-1中∠APN的度数;
(2)、图10-2中,∠APN的度数是 , 图10-3中∠BPN的度数是。
(3)、试探索∠APN的度数与正多边形边数n的关系(直接写答案)
27. 如图,⊙O半径为4cm,其内接正六边形ABCDEF,点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向终点F,C运动,连接PB,QE,PE,BQ.设运动时间为t(s).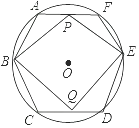 (1)、求证:四边形PEQB为平行四边形;(2)、填空:
(1)、求证:四边形PEQB为平行四边形;(2)、填空:①当t=s时,四边形PBQE为菱形;
②当t=s时,四边形PBQE为矩形.