初中数学苏科版九年级上学期期中复习专题4 圆的有关概念与基本性质
试卷更新日期：2021-11-02 类型：复习试卷
一、单选题
-
1. 下列说法中，不正确的是（ ）A、直径是最长的弦 B、同圆中，所有的半径都相等 C、圆既是轴对称图形又是中心对称图形 D、长度相等的弧是等弧2. 下列说法：①直径是弦；②弦是直径；③半径相等的两个半圆是等弧；④长度相等的两条弧是等弧；⑤半圆是弧，但弧不一定是半圆．正确的说法有（ ）A、1个 B、2个 C、3个 D、4个3. 下列说法：①三点确定一个圆；②圆中最长弦是直径；③长度相等的弧是等弧；④三角形只有一个外接圆.其中真命题有（ ）A、4个 B、3个 C、2个 D、1个4. 给出下列命题：
①弦是直径；②圆上两点间的距离叫弧；③长度相等的两段弧是等弧；④圆心角的度数与它所对的弧的度数相等；⑤圆是轴对称图形，不是中心对称图形；⑥直径是弦.其中正确的个数为（ ）
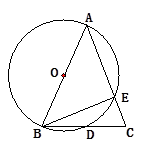
A、1 B、2 C、3 D、45. 如图，点A，B，C均在⊙O上，当∠OBC=40°时，∠A的度数是（ ）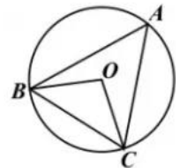
A、50° B、55° C、60° D、65°6. 已知，如图， ，下列结论不一定成立的是（ ）
A、 B、 C、 D、 都是等边三角形7. 如图，AB是⊙O的直径，点C，D在⊙O上， ＝ ，OD∥AC，下列结论错误的是（ ）
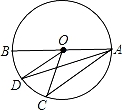A、∠C＝∠D B、∠BOD＝∠COD C、∠BAD＝∠CAD D、∠BOD＝∠BAC8. 如图，AB是⊙O的直径， ，∠COD=34°，则∠AOE的度数是（ ）
A、51° B、56° C、68° D、78°9.如图，⊙O的半径为4，△ABC是⊙O的内接三角形，连接OB、OC．若∠BAC与∠BOC互补，则弦BC的长为（ ）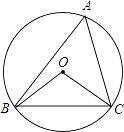
A、3 B、4 C、5 D、610. 如图，AD是⊙O的直径， ，若∠AOB＝40°，则圆周角∠BPC的度数是（ ）
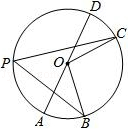A、40° B、50° C、60° D、70°11. 如图，在⊙O中，AB是直径，CD是弦，AB⊥CD，垂足为E，连接CO，AD，∠BAD=20°，则下列说法中正确的是（ ）
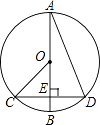A、AD=2OB B、CE=EO C、∠OCE=40° D、∠BOC=2∠BAD12. 如图，⊙O的直径CD＝20，AB是⊙O的弦，AB⊥CD，垂足为M，OM：OD＝3：5，则AB的长为（ ）
A、8 B、12 C、16 D、213. 如图，⊙O的半径OD垂直于弦AB，垂足为点C，连接AO并延长交⊙O于点E，连接BE，CE．若AB=8，CD=2，则△BCE的面积为（ ）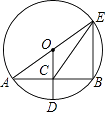
A、12 B、15 C、16 D、1814. 一块圆形宣传标志牌如图所示，点A，B，C在⊙O上，CD垂直平分AB于点D，现测得AB=8dm，DC=2dm，则圆形标志牌的半径为（ ）
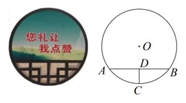A、6dm B、5dm C、4dm D、3dm15. 如图，AC是⊙O的直径，弦BD⊥AO于E，连接BC，过点O作OF⊥BC于F，若BD=8cm，AE=2cm，则OF的长度是（ ）
A、3cm B、 cm C、2.5cm D、 cm16. 如图所示，AB是⊙O的一条弦，OD⊥AB，垂足为C，交⊙O于点D，点E在优弧AB上． 若∠AOD=52°，则∠DEB的度数为（ ）
A、52° B、40° C、26° D、45°二、填空题
-
17. 过四边形的任意三个顶点能画圆的个数最多为个．18. 如图，在 中， 为 直径， 为圆上一点，若 ，则 的度数为 ．
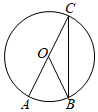19. 如图，AB是⊙O的直径，CD是⊙O的弦，AB、CD的延长线交于E点，若AB=2DE，∠E=18°，则∠AOC的度数为度．
20. 如图，AB为⊙O直径，点C、D在⊙O上，已知∠AOD=50°，AD∥OC，则∠BOC=度．
21. 如图，在平面直角坐标系中，已知 经过原点 ，与 轴、 轴分别交于 、 两点，点 坐标为 ， 与 交于点 ， ，则圆中阴影部分的面积为.
22. 如图1，小敏利用课余时间制作了一个脸盆架，图2是它的截面图，垂直放置的脸盆与架子的交点为A，B，AB=40cm，脸盆的最低点C到AB的距离为10cm，则该脸盆的半径为cm．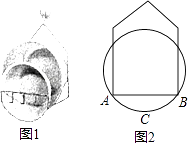
23. 如图，AC是⊙O的直径，弦BD⊥AC于点E，连接BC过点O作OF⊥BC于点F，若BD＝12cm，AE＝4cm，则OF的长度是cm.
三、综合题
