湘教版初中数学九上第3章 图形的相似 基础过关演练
试卷更新日期:2021-11-02 类型:同步测试
一、单选题
-
1. 如图,在 中, ,四边形 的面积为21,则 的面积是( )
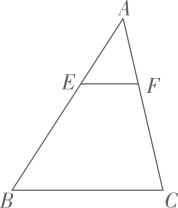 A、 B、25 C、35 D、632. 如图,在△ABC中,DE∥AB,且 = ,则 的值为( )
A、 B、25 C、35 D、632. 如图,在△ABC中,DE∥AB,且 = ,则 的值为( ) A、 B、 C、 D、3. 如图,△ABC与△DEF位似,点O为位似中心.已知OA:OD=1:2,则△ABC与△DEF的面积比为( )
A、 B、 C、 D、3. 如图,△ABC与△DEF位似,点O为位似中心.已知OA:OD=1:2,则△ABC与△DEF的面积比为( ) A、1:2 B、1:3 C、1:4 D、1:54. 在如图所示的网格中,以点O为位似中心,四边形 的位似图形是( )
A、1:2 B、1:3 C、1:4 D、1:54. 在如图所示的网格中,以点O为位似中心,四边形 的位似图形是( )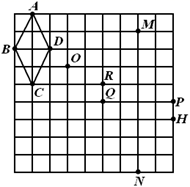 A、四边形 B、四边形 C、四边形 D、四边形5. 生活中到处可见黄金分割的美,如图,在设计人体雕像时,使雕像的腰部以下a与全身 的高度比值接近0.618,可以增加视觉美感,若图中 为2米,则a约为( )
A、四边形 B、四边形 C、四边形 D、四边形5. 生活中到处可见黄金分割的美,如图,在设计人体雕像时,使雕像的腰部以下a与全身 的高度比值接近0.618,可以增加视觉美感,若图中 为2米,则a约为( )
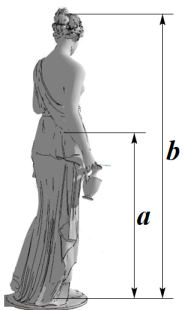 A、1.24米 B、1.38米 C、1.42米 D、1.62米6. 若 ,且 ,则 的值是( )A、4 B、2 C、20 D、147. 学校门口的栏杆如图所示,栏杆从水平位置 绕 点旋转到 位置,已知 , ,垂足分别为 , , , , ,则栏杆 端应下降的垂直距离 为( )
A、1.24米 B、1.38米 C、1.42米 D、1.62米6. 若 ,且 ,则 的值是( )A、4 B、2 C、20 D、147. 学校门口的栏杆如图所示,栏杆从水平位置 绕 点旋转到 位置,已知 , ,垂足分别为 , , , , ,则栏杆 端应下降的垂直距离 为( )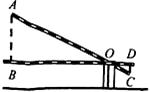 A、 B、 C、 D、8. 若△ABC的每条边长增加各自的10%得△A′B′C′,则∠B′的度数与其对应角∠B的度数相比( )A、增加了10% B、减少了10% C、增加了(1+10%) D、没有改变9.
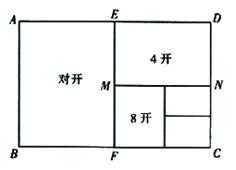
A、 B、 C、 D、8. 若△ABC的每条边长增加各自的10%得△A′B′C′,则∠B′的度数与其对应角∠B的度数相比( )A、增加了10% B、减少了10% C、增加了(1+10%) D、没有改变9.如图所示,一般书本的纸张是在原纸张多次对开得到的.矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,依此类推.若各种开本的矩形都相似,那么等于( ).
 A、0.618 B、 C、 D、210. 若2a=3b=4c,且abc≠0,则的值是( )A、2 B、﹣2 C、3 D、﹣3
A、0.618 B、 C、 D、210. 若2a=3b=4c,且abc≠0,则的值是( )A、2 B、﹣2 C、3 D、﹣3二、填空题
-
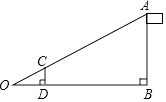
11. 若 ,则 .12. 如图,数学活动小组为了测量学校旗杆AB的高度,使用长为2m的竹竿CD作为测量工具.移动竹竿,使竹竿顶端的影子与旗杆顶端的影子在地面O处重合,测得OD=4m,BD=14m,则旗杆AB的高为m.
 13. 湖南地图出版社首发的竖版《中华人民共和国地图》,将南海诸岛与中国大陆按同比例尺1:6700000表示出来,使读者能够全面、直观地认识我国版图,若在这种地图上量得我国南北的图上距离是82.09厘米,则我国南北的实际距离大约是千米(结果精确到1千米)14.
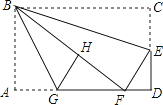
13. 湖南地图出版社首发的竖版《中华人民共和国地图》,将南海诸岛与中国大陆按同比例尺1:6700000表示出来,使读者能够全面、直观地认识我国版图,若在这种地图上量得我国南北的图上距离是82.09厘米,则我国南北的实际距离大约是千米(结果精确到1千米)14.如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
①∠EBG=45°;②△DEF∽△ABG;③S△ABG= S△FGH;④AG+DF=FG.
其中正确的是 . (把所有正确结论的序号都选上)
三、作图题
-
15. 如图,已知在正方形ABCD中,M是BC边上一定点,连接AM,请用尺规作图法,在AM上求作一点P,使得△DPA∽△ABM(不写做法保留作图痕迹)
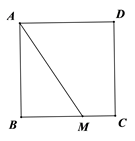 16.
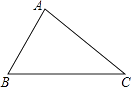
16.如图,已知△ABC,∠BAC=90°,请用尺规过点A作一条直线,使其将△ABC分成两个相似的三角形(保留作图痕迹,不写作法)
四、解答题
-
17.
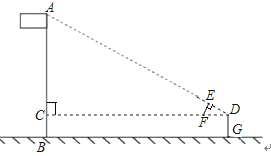
如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,求旗杆的高度.
五、综合题
-
18. 如图,四边形ABCD是⊙O的内接四边形, ,AC为直径,DE⊥BC,垂足为E.
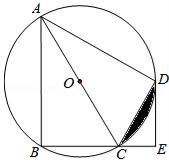 (1)、求证:CD平分∠ACE;(2)、若AC=9,CE=3,求CD的长.19. 如图,在四边形ABCD中,AC平分∠DAB,AC2=AB•AD,∠ADC=90°,点E为AB的中点.
(1)、求证:CD平分∠ACE;(2)、若AC=9,CE=3,求CD的长.19. 如图,在四边形ABCD中,AC平分∠DAB,AC2=AB•AD,∠ADC=90°,点E为AB的中点.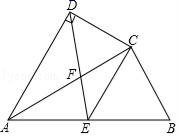 (1)、求证:△ADC∽△ACB.(2)、若AD=2,AB=3,求 的值.20. 如图,为测量学校围墙外直立电线杆AB的高度,小亮在操场上点C处直立高3m的竹竿CD,然后退到点E处,此时恰好看到竹竿顶端D与电线杆顶端B重合;小亮又在点C1处直立高3m的竹竿C1D1 , 然后退到点E1处,此时恰好看到竹竿顶端D1与电线杆顶端B重合.小亮的眼睛离地面高度EF=1.5m,量得CE=2m,EC1=6m,C1E1=3m.
(1)、求证:△ADC∽△ACB.(2)、若AD=2,AB=3,求 的值.20. 如图,为测量学校围墙外直立电线杆AB的高度,小亮在操场上点C处直立高3m的竹竿CD,然后退到点E处,此时恰好看到竹竿顶端D与电线杆顶端B重合;小亮又在点C1处直立高3m的竹竿C1D1 , 然后退到点E1处,此时恰好看到竹竿顶端D1与电线杆顶端B重合.小亮的眼睛离地面高度EF=1.5m,量得CE=2m,EC1=6m,C1E1=3m.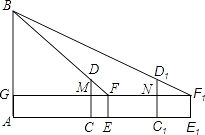 (1)、△FDM∽△ , △F1D1N∽△(2)、求电线杆AB的高度.21. 定义:我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
(1)、△FDM∽△ , △F1D1N∽△(2)、求电线杆AB的高度.21. 定义:我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.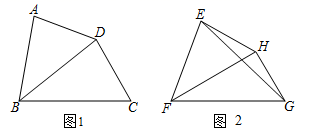 (1)、如图1,在四边形 中, , ,对角线 平分 .求证: 是四边形 的“相似对角线”;(2)、如图2,已知 是四边形 的“相似对角线”, .连接 ,若 的面积为 ,求 的长.
(1)、如图1,在四边形 中, , ,对角线 平分 .求证: 是四边形 的“相似对角线”;(2)、如图2,已知 是四边形 的“相似对角线”, .连接 ,若 的面积为 ,求 的长.
-