内蒙古赤峰市宁城县2021-2022学年高三上学期理数10月考试卷

试卷更新日期：2021-11-02 类型：月考试卷

进入出卷网下载

一、单选题

1. 已知全集 $U = {1 ， 2 ， 3 ， 4 ， 5 ， 6}$ ，集合 $A = {1 ， 3}$ ，集合 $B = {3 ， 4 ， 5}$ ，则集合 $B \cap (∁_{U} A) =$ （）

A、 ${4 ， 5}$ B、{1} C、 ${1 ， 2}$ D、 ${1 ， 2 ， 3 ， 6}$

查看试题解析
2. 设i为虚数单位， $a \in R$ ，若 $(1 - i) (1 - a i)$ 为纯虚数，则复数 $1 - a i$ 的模是（）

A、 $\sqrt{2}$ B、2 C、1 D、0

查看试题解析
3. 已知命题p：∀x∈（0，+∞），x＞sinx，命题 $q ： \exists x \in R ， {(\frac{1}{2})}^{x} = \log_{\frac{1}{2}} x$ ，则下列命题中的真命题为（）

A、￢q B、p∧q C、（￢p）∧q D、（￢p）∨（¬q）

查看试题解析
4. 已知等差数数列 ${a_{n}}$ 的前项和为 $S_{n}$ ,若 $a_{3} + a_{7} = 6$ ,则 $S_{9}$ 等于（）

A、15 B、18 C、27 D、39

查看试题解析
5. 已知 $\frac{5 π}{12}$ 是函数 $f (x) = \sin (2 x + θ) (0 < θ < \frac{π}{2})$ 的零点，则函数 $f (x)$ 的一条对称轴是（）

A、 $x = \frac{π}{3}$ B、 $x = \frac{π}{12}$ C、 $x = - \frac{π}{12}$ D、 $x = \frac{π}{6}$

查看试题解析
6. 定义在R上的奇函数f(x)满足f(x+2)=f(x)，当 $x \in (- 1 ， 0)$ 时， $f (x) = e^{- x}$ ，则 $f (\frac{9}{2}) =$ （）

A、 $\sqrt{e}$ B、 $- \sqrt{e}$ C、 $\frac{1}{\sqrt{e}}$ D、 $- \frac{1}{\sqrt{e}}$

查看试题解析
7. 设 $l$ 是一条直线， $α$ ， $β$ 是两个平面，下列结论正确的是（）

A、若 $l // α$ ， $l // β$ ，则 $α // β$ B、若 $α ⊥ β$ ， $l // α$ ，则 $l ⊥ β$ C、若 $l // α$ ， $l ⊥ β$ ，则 $α ⊥ β$ D、若 $α ⊥ β$ ， $l ⊥ α$ ，则 $l // β$

查看试题解析
8. 2020年9月4日至9日，中国国际服务贸易交易会在北京国家会议中心召开，某企业安排9名职工到4个展区进行产品宣传，要求甲展区安排1人，乙展区安排2人，剩下两个展区各安排3人，不同的安排方法共有（）

A、3680种 B、4800种 C、5040种 D、7200种

查看试题解析
9. 已知 $M_{1}$ ， $M_{2}$ 是双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左右顶点， $P$ 为该双曲线上任一点（与 $M_{1}$ ， $M_{2}$ 不重合），已知 $P M_{1}$ 与 $P M_{2}$ 斜率之积为 $\frac{4}{9}$ ，则该双曲线的渐近线方程为（）

A、 $3 x \pm \sqrt{5} y = 0$ B、 $\sqrt{5} x \pm 3 y = 0$ C、 $3 x \pm 2 y = 0$ D、 $2 x \pm 3 y = 0$

查看试题解析
10. 某几何体的三视图如下图所示，则该几何体的体积为（）

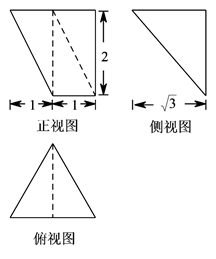A、 $\sqrt{3}$ B、 $\frac{11 \sqrt{3}}{6}$ C、 $\frac{5 \sqrt{3}}{3}$ D、 $\frac{4 \sqrt{3}}{3}$

查看试题解析
11. 已知函数 $y = f (x)$ 对任意的 $x \in (0 ， π)$ 满足 $f^{'} (x) \cos x > f (x) \sin x$ （其中 $f^{'} (x)$ 为函数 $f (x)$ 的导函数），则下列不等式成立的是（）

A、 $f (\frac{π}{6}) > \sqrt{3} f (\frac{π}{3})$ B、 $f (\frac{π}{6}) < \sqrt{3} f (\frac{π}{3})$ C、 $\sqrt{3} f (\frac{π}{6}) > f (\frac{π}{3})$ D、 $\sqrt{3} f (\frac{π}{6}) < f (\frac{π}{3})$

查看试题解析
12. 英国著名物理学家牛顿用“作切线”的方法求函数零点时，给出的“牛顿数列”在航空航天中应用广泛，若数列 ${x_{n}}$ 满足 $x_{n + 1} = x_{n} - \frac{f (x_{n})}{f^{'} (x_{n})}$ ，则称数列 ${x_{n}}$ 为牛顿数列.如果函数 $f (x) = x^{2} - x - 2$ ，数列 ${x_{n}}$ 为牛顿数列，设 $a_{n} = \ln \frac{x_{n} - 2}{x_{n} + 1}$ 且 $a_{1} = - 1$ ， $x_{n} > 2$ ，数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，则 $S_{2021} =$ （）

A、 $2^{2021} - 1$ B、 $1 - 2^{2021}$ C、 ${(\frac{1}{2})}^{2021} - \frac{1}{2}$ D、 ${(\frac{1}{2})}^{2021} - 2$

查看试题解析

二、填空题

13. 若非零向量 $\vec{a}$ ， $\vec{b}$ 满足 $| \vec{a} | = | \vec{b} |$ ， $(\sqrt{2} \vec{a} - 2 \vec{b}) \cdot \vec{a} = 0$ ，则与 $\vec{a}$ ， $\vec{b}$ 的夹角为.

查看试题解析
14. 某次知识竞赛规则如下：在主办方预设的5个问题中，选手若能连续正确回答出两个问题，即停止答题，晋级下一轮．假设某选手正确回答每个问题的概率都是0.8，且每个问题的回答结果相互独立，则该选手恰好回答了4个问题就晋级下一轮的概率等于．

查看试题解析
15. 设抛物线 $y^{2} = 2 p x (p > 0)$ 的焦点为 $F$ ，过点 $F$ 且倾斜角为 $\frac{π}{4}$ 的直线 $l$ 与抛物线相交于 $A$ ， $B$ 两点，若以 $A B$ 为直径的圆过点 $(- \frac{p}{2} ， 2)$ ，则该抛物线的方程为．

查看试题解析
16. 若 $f (x)$ 的图像上存在两点 $AB$ 关于原点对称，则点对 $[A ， B]$ 称为函数 $f (x)$ 的“友情点对”（点对 $[A ， B]$ 与 $[B ， A]$ 视为同一个“友情点对”.）若 $f (x) = {\begin{array}{l} x^{3} \ln x ， x > 0 \\ a x^{2} ， x \leq 0 \end{array}$ ，恰有两个“友情点对”，则实数 $a$ 的取值范围是.

查看试题解析

三、解答题

17. $Δ A B C$ 的内角 $A$ ， $B$ ， $C$ 的对边分别为 $a$ ， $b$ ， $c$ ，已知 $c \cos B = (3 a - b) \cos C$ .

(1)、求 $\sin C$ 的值；

(2)、若 $c = 2 \sqrt{6}$ ， $b - a = 2$ ，求 $Δ A B C$ 的面积.

查看试题解析
18. 某校在一次期末数学测试中，为统计学生的考试情况，从学校的2000名学生中随机抽取50名学生的考试成绩，被测学生成绩全部介于65分到145分之间(满分150分)，将统计结果按如下方式分成八组：第一组 $[65$ ， $75)$ ，第二组 $[75$ ， $85)$ ， $\dots \dots$ 第八组 $[135$ ， $145]$ ，如图是按上述分组方法得到的频率分布直方图的一部分.

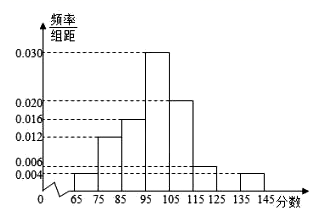(1)、求第七组的频率，并完成频率分布直方图；

(2)、用样本数据估计该校的2000名学生这次考试成绩的平均分(同一组中的数据用该组区间的中点值代表该组数据平均值)；

(3)、若从样本成绩属于第六组和第八组的所有学生中随机抽取2名，求他们的分差的绝对值小于10分的概率.

查看试题解析
19. 已知直三棱柱 $A B C - A^{'} B^{'} C^{'}$ ，底面 $△ A B C$ 是边长为2的等边三角形， $A A^{'} = 2 \sqrt{3}$ ， $E$ 在棱 $B B^{'}$ 上，且 $B B^{'} = 4 B E$ ， $O$ 为棱 $A C$ 的中点.

(1)、证明： $O E ⊥$ 面 $A^{'} C^{'} B$ ；

(2)、求锐二面角 $C - A^{'} B - C^{'}$ 的平面角的余弦值.

查看试题解析
20. 已知 $F_{1}$ ， $F_{2}$ 是椭圆 $E$ ： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左、右焦点， $F_{2}$ 恰好与抛物线 $y^{2} = 4 x$ 的焦点重合，过椭圆 $E$ 的左焦点 $F_{1}$ 且与 $x$ 轴垂直的直线被椭圆 $E$ 截得的线段长为3．

(1)、求椭圆 $E$ 的方程；

(2)、已知点 $P (1 ， \frac{3}{2})$ ，直线 $l$ ： $x = 4$ ，过 $F_{2}$ 斜率为 $k$ 的直线与椭圆 $E$ 交于 $A$ ， $B$ 两点，与直线 $l$ 交于 $M$ 点，若直线 $P A$ ， $P B$ ， $P M$ 的斜率分别是 $k_{1}$ ， $k_{2}$ ， $k_{3}$ ，求证：无论 $k$ 取何值，总满足 $k_{3}$ 是 $k_{1}$ 和 $k_{2}$ 的等差中项．

查看试题解析
21. 已知函数 $f (x) = \frac{x + 1}{e^{2 x}}$ .

(1)、求 $f (x)$ 在点 $(1 ， f (1))$ 处的切线方程；

(2)、设函数 $g (x) = \frac{f (x)}{x + 1} \cdot \ln (2 x + a)$ ，当 $a \leq 2$ 时，求证： $g (x) < 1$ .

查看试题解析
22. 极坐标系的极点为直角坐标系 $x O y$ 的原点，极轴为 $x$ 轴的正半轴，两极坐标系中的长度单位相同．已知曲线 $C$ 的极坐标方程为 $ρ = 2 \sin θ$ ， $θ \in [0 ， 2 π)$ ．

(1)、求曲线 $C$ 的直角坐标方程；

(2)、在曲线 $C$ 上求一点，使它到直线 $l$ ： ${\begin{array}{l} x = \sqrt{3} t + \sqrt{3} \\ y = - 3 t + 2 \end{array}$ （ $t$ 为参数）的距离最短，写出 $D$ 点的直角坐标．

查看试题解析
23. 已知函数 $f (x) = | x + a |$ （ $a \in R$ ）.

(1)、若 $f (x) \geq | 2 x + 3 |$ 的解集为 $[- 3 ， - 1]$ ，求 $a$ 的值；

(2)、若 $\forall x \in R$ ，不等式 $f (x) + | x - a | \geq a^{2} - 2 a$ 恒成立，求实数 $a$ 的取值范围.

查看试题解析