浙教版初中数学七年级上册第6章 图形的初步知识 单元检测卷
试卷更新日期:2021-11-02 类型:单元试卷
一、单选题
-
1. 下列几何体中,圆柱是( )A、
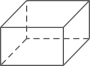 B、
B、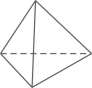 C、
C、 D、
D、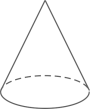 2. 甲、乙两地之间有四条路可走(如图),那么最短路线的序号是( )
2. 甲、乙两地之间有四条路可走(如图),那么最短路线的序号是( )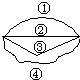 A、① B、② C、③ D、④3. 用量角器测量
A、① B、② C、③ D、④3. 用量角器测量 的度数,操作正确的是( ) A、
的度数,操作正确的是( ) A、 B、
B、 C、
C、 D、
D、 4. 若 , ,则 与 的大小关系是( )A、 B、 C、 D、无法判断5. 在下图中,∠1和∠2是对顶角的是( )A、
4. 若 , ,则 与 的大小关系是( )A、 B、 C、 D、无法判断5. 在下图中,∠1和∠2是对顶角的是( )A、 B、
B、 C、
C、 D、
D、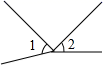 6. 如图,经过创平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是( )
6. 如图,经过创平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是( ) A、两点确定一条直线 B、两点之间线段最短 C、垂线段最短 D、在同一平面内,过一点有且只有一条直线与已知直线垂直7. 在线段AB上取一点C,使AC= AB,再在线段AB的延长线上取一点D,使DB= AD,则线段BC的长度是线段DC长度的( )A、 B、 C、 D、8. 已知∠AOB= 60°,以O为圆心,以任意长为半径作弧,交OA,OB于点M,N,分别以点M,N为圆心,以大于 MN的长度为半径作弧,两弧在∠AOB内交于点P,以OP为边作∠POC=15°,则∠BOC的度数为( )A、15° B、45° C、15°或30° D、15°或45°9. 一个角的度数等于60°20′,那么它的余角等于( )A、40°80′ B、39°80′ C、30°40′ D、29°40′10. 已知 ,则 的补角是( ).A、 B、 C、 D、
A、两点确定一条直线 B、两点之间线段最短 C、垂线段最短 D、在同一平面内,过一点有且只有一条直线与已知直线垂直7. 在线段AB上取一点C,使AC= AB,再在线段AB的延长线上取一点D,使DB= AD,则线段BC的长度是线段DC长度的( )A、 B、 C、 D、8. 已知∠AOB= 60°,以O为圆心,以任意长为半径作弧,交OA,OB于点M,N,分别以点M,N为圆心,以大于 MN的长度为半径作弧,两弧在∠AOB内交于点P,以OP为边作∠POC=15°,则∠BOC的度数为( )A、15° B、45° C、15°或30° D、15°或45°9. 一个角的度数等于60°20′,那么它的余角等于( )A、40°80′ B、39°80′ C、30°40′ D、29°40′10. 已知 ,则 的补角是( ).A、 B、 C、 D、二、填空题
-
11. 要把一根木条在墙上钉牢,至少需要2枚钉子.其中蕴含的数学道理是.12. 如图,把弯曲的公路改直,能够缩短行程,这样做的道理是 .
 13. 飞机表演的“飞机拉线”用数学知识解释为 , 三角板绕它的一条直角边旋转一周,形成一个圆锥体,这说明了 .14. 计算: 结果用度、分、秒表示15. 已知∠A=30°45',∠B=30.45°,则∠A∠B.(填“>”、“<”或“=”)16. 已知:OA⊥OC,∠AOB:∠BOC=1:3,则∠BOC的度数为 .
13. 飞机表演的“飞机拉线”用数学知识解释为 , 三角板绕它的一条直角边旋转一周,形成一个圆锥体,这说明了 .14. 计算: 结果用度、分、秒表示15. 已知∠A=30°45',∠B=30.45°,则∠A∠B.(填“>”、“<”或“=”)16. 已知:OA⊥OC,∠AOB:∠BOC=1:3,则∠BOC的度数为 .三、解答题
-
17. 一个角的补角比这个角的余角的3倍少50°,求这个角的度数.18. 如图,已知直线 , 相交于点 , 平分 , 平分 .若 ,
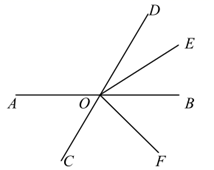 (1)、求 的度数;(2)、求 的度数.19. 如图1,AB⊥BC于点B , CD⊥BC于点C , 点E在线段BC上,且AE⊥DE .
(1)、求 的度数;(2)、求 的度数.19. 如图1,AB⊥BC于点B , CD⊥BC于点C , 点E在线段BC上,且AE⊥DE . (1)、求证:∠EAB=∠CED;(2)、如图2,AF、DF分别平分∠BAE和∠CDE , 则∠F的度数是(直接写出答案即可);(3)、如图3,EH平分∠CED , EH的反向延长线交∠BAE的平分线AF于点G . 求证:EG⊥AF . (提示:三角形内角和等于180°)20. 作图题:尺规作图,保留作图痕迹.
(1)、求证:∠EAB=∠CED;(2)、如图2,AF、DF分别平分∠BAE和∠CDE , 则∠F的度数是(直接写出答案即可);(3)、如图3,EH平分∠CED , EH的反向延长线交∠BAE的平分线AF于点G . 求证:EG⊥AF . (提示:三角形内角和等于180°)20. 作图题:尺规作图,保留作图痕迹.如图,已知三角形ABC和给出的∠MB′N,∠MB′N=∠ABC.
 (1)、在射线B′N上截取B′C′=BC;(2)、在B′C′上方作∠EC′B′=∠ACB,C′E与B′M相交于点A′.21. 如图,点C、D是线段AB上两点, ,点D为AB的中点.
(1)、在射线B′N上截取B′C′=BC;(2)、在B′C′上方作∠EC′B′=∠ACB,C′E与B′M相交于点A′.21. 如图,点C、D是线段AB上两点, ,点D为AB的中点. (1)、如图1所示,若 ,求线段CD的长;(2)、如图2所示,若E为AC的中点, ,求线段AB的长.22. 如图,平面上有三个点 , , .(1)、根据下列语句顺次画图.
(1)、如图1所示,若 ,求线段CD的长;(2)、如图2所示,若E为AC的中点, ,求线段AB的长.22. 如图,平面上有三个点 , , .(1)、根据下列语句顺次画图.①画射线 , ;
②连接线段 ;
③过点 画直线 ,垂足为 ;
(2)、请回答:图形中点 到直线 的距离是线段 . 23. 在△ABC中,∠BCA>∠BAC,三个内角的平分线交于点O.
23. 在△ABC中,∠BCA>∠BAC,三个内角的平分线交于点O.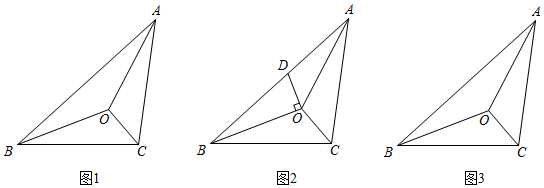 (1)、填空:如图1,若∠BAC=36°,则∠BOC的大小为;(2)、点D在BA,AC边上运动.
(1)、填空:如图1,若∠BAC=36°,则∠BOC的大小为;(2)、点D在BA,AC边上运动.①如图2,当点D在BA边上运动时,连接OD,若OD⊥OB.试说明:∠ADO=∠AOC;
②如图3,BO的延长线交AC于点E,当点D在AC边上运动(不与点E重合)时,过点D作DP⊥BO,垂足为点P,请在图3中画出符合条件的图形,并探索∠ADP、∠ACB、∠BAC者之间的数量关系.
24. 已知 , 为 内部的一条射线, . (1)、如图1,若 平分 , 为 内部的一条射线, ,求 的度数;(2)、如图2,若射线 绕着 点从 开始以每秒 的速度顺时针旋转至 结束、 绕着 点从 开始以每秒 的速度逆时针旋转至 结束,当一条射线到达终点时另一条射线也停止运动.若运动时间为 秒,当 时,求 的值;(3)、若射线 绕着 点从 开始以每秒 的速度逆时针旋转至 结束,在旋转过程中, 平分 ,试问 在某时间段内是否为定值;若不是,请说明理由;若是,请补全图形,并直接写出这个定值以及 相应所在的时间段.(本题中的角均为大于 且小于 的角)
(1)、如图1,若 平分 , 为 内部的一条射线, ,求 的度数;(2)、如图2,若射线 绕着 点从 开始以每秒 的速度顺时针旋转至 结束、 绕着 点从 开始以每秒 的速度逆时针旋转至 结束,当一条射线到达终点时另一条射线也停止运动.若运动时间为 秒,当 时,求 的值;(3)、若射线 绕着 点从 开始以每秒 的速度逆时针旋转至 结束,在旋转过程中, 平分 ,试问 在某时间段内是否为定值;若不是,请说明理由;若是,请补全图形,并直接写出这个定值以及 相应所在的时间段.(本题中的角均为大于 且小于 的角)