初中数学浙教版九年级上册专题复习:圆
试卷更新日期:2021-11-02 类型:复习试卷
一、单选题
-
1. 如图,一块含30°角的直角三角板ABC绕点C顺时针旋转到△A′B′C , 当B , C , A′在一条直线上时,三角板ABC的旋转角度为( )
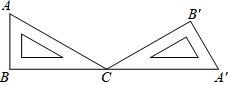 A、150° B、120° C、60° D、30°2. 如图,破残的轮子上,弓形的弦AB为4m,高CD为1m,则这个轮子的半径长为( )
A、150° B、120° C、60° D、30°2. 如图,破残的轮子上,弓形的弦AB为4m,高CD为1m,则这个轮子的半径长为( )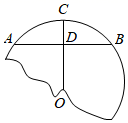 A、 m B、 m C、5m D、 m3. 已知一个扇形的圆心角为 ,半径为 ,则该扇形的弧长为( )A、 B、 C、 D、4. 如图,在等边三角形网格中,△ABC的顶点都在格点上,点P,Q,M是AB与格线的交点,则△ABC的外心是( )
A、 m B、 m C、5m D、 m3. 已知一个扇形的圆心角为 ,半径为 ,则该扇形的弧长为( )A、 B、 C、 D、4. 如图,在等边三角形网格中,△ABC的顶点都在格点上,点P,Q,M是AB与格线的交点,则△ABC的外心是( ) A、点P B、点Q C、点M D、点N5. 如图, 为⊙O的直径,点C、D是 的三等分点, ,则 的度数为( )
A、点P B、点Q C、点M D、点N5. 如图, 为⊙O的直径,点C、D是 的三等分点, ,则 的度数为( ) A、40° B、60° C、80° D、120°6. 如图,AB为 的直径,C , D为 上的两点,若 ,则 的度数为( )
A、40° B、60° C、80° D、120°6. 如图,AB为 的直径,C , D为 上的两点,若 ,则 的度数为( ) A、 B、 C、 D、7. 如图,四边形ABCD内接于⊙O,E为CD延长线上一点,若∠B=110°,则∠ADE的度数为( )
A、 B、 C、 D、7. 如图,四边形ABCD内接于⊙O,E为CD延长线上一点,若∠B=110°,则∠ADE的度数为( )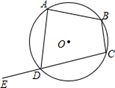 A、35° B、55° C、70° D、110°8. 如图,正六边形ABCDEF内接于 ,已知 的 半径为2,则圆心O到边AB的距离是( )
A、35° B、55° C、70° D、110°8. 如图,正六边形ABCDEF内接于 ,已知 的 半径为2,则圆心O到边AB的距离是( )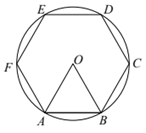 A、2 B、1 C、 D、9. 某校科技实践社团制作实践设备,小明的操作过程如下:①小明取出老师提供的圆形细铁环,先通过在圆一章中学到的知识找到圆心O,再任意找出圆O的一条直径标记为AB(如图1),测量出AB=4分米;②将圆环进行翻折使点B落在圆心O的位置,翻折部分的圆环和未翻折的圆环产生交点分别标记为C、D(如图2);③用一细橡胶棒连接C、D两点(如图3);④计算出橡胶棒CD的长度.
A、2 B、1 C、 D、9. 某校科技实践社团制作实践设备,小明的操作过程如下:①小明取出老师提供的圆形细铁环,先通过在圆一章中学到的知识找到圆心O,再任意找出圆O的一条直径标记为AB(如图1),测量出AB=4分米;②将圆环进行翻折使点B落在圆心O的位置,翻折部分的圆环和未翻折的圆环产生交点分别标记为C、D(如图2);③用一细橡胶棒连接C、D两点(如图3);④计算出橡胶棒CD的长度.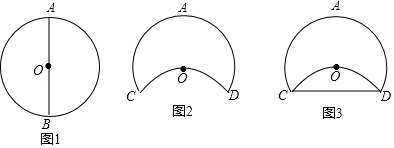
小明计算橡胶棒CD的长度为( )
A、2 分米 B、2 分米 C、3 分米 D、3 分米10. 如图, 是 的直径, , 是 的半径, ,点D在 上, ,点P是半径 上的一个动点,则 的最小值为( ) A、1 B、 C、 D、
A、1 B、 C、 D、二、填空题
-
11. 在平面内, 的半径为 ,点 到圆心 的距离为 ,则点 与 的位置关系是点 在 . (填“圆内”“圆外”或“圆上”).12. 如图所示,△ADE是将△ABC绕点A顺时针旋转一定角度α(0°<α<90°)得到的,AC与DE相交于点M , 其中∠B=70°,∠C=30°,现要使得△ADM为等腰三角形,则旋转角α的度数为 .
 13. 如图, 的直径 ,弦 ,垂足为 , ,则 的长为.
13. 如图, 的直径 ,弦 ,垂足为 , ,则 的长为.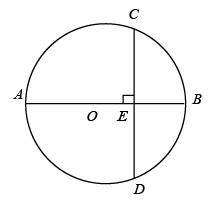 14. 如图,A,B,C,D是⊙O上的四个点, = ,若∠AOB=58°,则∠BDC=度.
14. 如图,A,B,C,D是⊙O上的四个点, = ,若∠AOB=58°,则∠BDC=度.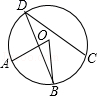 15. 如图,以 的边 为直径的 分别交 、 于点 、 ,连接 、 ,若 ,则 .
15. 如图,以 的边 为直径的 分别交 、 于点 、 ,连接 、 ,若 ,则 .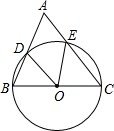 16. 如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,则图中三个扇形(即阴影部分)面积之和是cm2
16. 如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,则图中三个扇形(即阴影部分)面积之和是cm2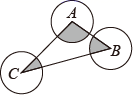
三、解答题
-
17.
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,连接PB,PD分别交CD于M,交AB于点N,且CM=BM,
(1)求证:CB∥PD;
(2)若BC=5,sin∠BPD= , 求⊙O的直径.
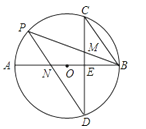 18.
18.如图③,点E,D分别是正三角形ABC,正四边形ABCM,正五边形ABCMN中以点C为顶点的一边延长线和另一边反向延长线上的点,且△ABE与△BCD能相互重合,DB的延长线交AE于点F.
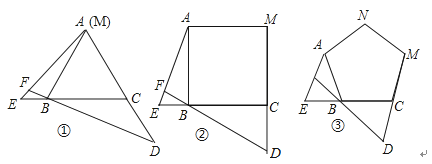 (1)、在图①中,求∠AFB的度数(2)、在图②中,∠AFB的度数为 度,图③中,∠AFB的度数为度
(1)、在图①中,求∠AFB的度数(2)、在图②中,∠AFB的度数为 度,图③中,∠AFB的度数为度
(3)、继续探索,可将本题推广到一般的正n边形情况,用含n的式子表示∠AFB的度数.19. 如图,在⊙O中,弦AB的长为8,圆心O到AB的距离为3. (1)、求⊙O的半径;(2)、若点P是AB上的一动点,试直接写出线段OP的取值范围.20. 如图,⊙O的两条弦AB、CD交于点E,OE平分∠BED.
(1)、求⊙O的半径;(2)、若点P是AB上的一动点,试直接写出线段OP的取值范围.20. 如图,⊙O的两条弦AB、CD交于点E,OE平分∠BED.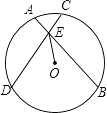 (1)、求证:AB=CD;(2)、若∠BED=60°,EO=2,求DE﹣AE的值.21. 如图,线段AB的端点在边长为1的正方形网格的格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC.
(1)、求证:AB=CD;(2)、若∠BED=60°,EO=2,求DE﹣AE的值.21. 如图,线段AB的端点在边长为1的正方形网格的格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC. (1)、请你用直尺和圆规在所给的网格中画出线段AC及点B经过的路径;(2)、若将此网格放在一平面直角坐标系中,已知点A的坐标为
(1)、请你用直尺和圆规在所给的网格中画出线段AC及点B经过的路径;(2)、若将此网格放在一平面直角坐标系中,已知点A的坐标为(1,3),点B的坐标为(﹣2,﹣1),则点C的坐标为;
(3)、线段AB在旋转到线段AC的过程中,点B经过的路径长为;(4)、若有一张与(3)中所说的区域形状相同的纸片,将它围成个圆锥的侧面,则该圆锥底面圆的半径长为 .22. 如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连结BC.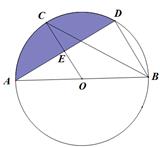 (1)、求证:AE=ED;(2)、若AB=8,∠CBD=30°,求图中阴影部分的面积.23. 如图
(1)、求证:AE=ED;(2)、若AB=8,∠CBD=30°,求图中阴影部分的面积.23. 如图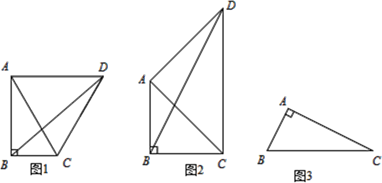
问题发现:
(1)、如图1,在Rt△ABC中,∠BAC=30°,∠ABC=90°,将线段AC绕点A逆时针旋转,旋转角α=2∠BAC, ∠BCD的度数是;线段BD,AC之间的数量关系是.(2)、在Rt△ABC中,∠BAC=45°,∠ABC=90°,将线段AC绕点A逆时针旋转,旋转角α=2∠BAC,请问(1)中的结论还成立吗?;(3)、如图3,在Rt△ABC中,AB=2,AC=4,∠BDC=90°,若点P满足PB=PC,∠BPC=90°,请直接写出线段AP的长度.24. 已知 是 上一点,过点 作不过圆心的弦 ,在劣弧 和优弧 上分别有动点 、 (不与 、 重合),连接 、 .若 . (1)、如图1,当 , , 时,求 的半径;(2)、在(1)的条件下,求四边形 的面积;(3)、如图2,连接 ,交 于点 ,点 在线段 上(不与 、 重合),连接 、 ,若 ,探究直线 与 的位置关系,并说明理由.
(1)、如图1,当 , , 时,求 的半径;(2)、在(1)的条件下,求四边形 的面积;(3)、如图2,连接 ,交 于点 ,点 在线段 上(不与 、 重合),连接 、 ,若 ,探究直线 与 的位置关系,并说明理由.