贵州省铜仁市石阡县2020-2021学年八年级上学期数学第三次月考试卷

试卷更新日期：2021-11-02 类型：月考试卷

进入出卷网下载

一、单选题

1. 在代数式 $\frac{3}{a} ， \frac{2 x - 3 y}{4} ， \frac{1}{2} (m - n) ， \frac{x - y}{x + y} ， \frac{1}{π}$ 中属于分式的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 计算 ${(- \frac{1}{2} {ab}^{2})}^{3}$ 的结果是（）

A、 $- \frac{3}{2} a^{3} b^{6}$ B、 $- \frac{1}{2} a^{3} b^{5}$ C、 $- \frac{1}{8} a^{3} b^{5}$ D、 $- \frac{1}{8} a^{3} b^{6}$

查看试题解析
3. 若分式 $\frac{x - 2}{x^{2} - 1}$ 的值为0，则x的值为（）

A、1 B、－1 C、±1 D、2

查看试题解析
4. 若三角形的两边长分别为6 ㎝，9 cm，则其第三边的长可能为（）

A、2㎝ B、3 cm C、7㎝ D、16 cm

查看试题解析
5. 如图，已知∠1=∠2，若用“SAS”证明△ACB≌△BDA，还需加上条件（）

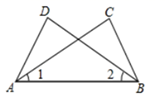A、AD ＝BC B、BD＝AC C、∠D＝∠C D、OA＝OB

查看试题解析
6. 将一副直角三角板，按如图所示叠放在一起，则图中∠ 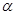的度数是（）

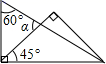A、45^o B、60^o C、75^o D、90^o

查看试题解析
7. 下列实数中是无理数的是（）

A、 $- 1$ B、 $\frac{1}{2}$ C、 $\sqrt{3}$ D、0

查看试题解析
8. 下列说法中，正确的个数是（）
①-64的立方根是-4；②49的算术平方根是±7；③ $\frac{1}{27}$ 的立方根为 $\frac{1}{3}$ ；④ $\frac{1}{16}$ 的一个平方根 $\pm \frac{1}{4}$ .

A、1 B、2 C、3 D、4

查看试题解析
9. 已知a的平方根是±8，则a的立方根是（）

A、2 B、4 C、±2 D、±4

查看试题解析
10. 如图，数轴上表示2、 $\sqrt{5}$ 的对应点分别记为C、B，点C是 $A B$ 的中点，则点A表示的数是（）

A、 $- \sqrt{5}$ B、 $2 - \sqrt{5}$ C、 $4 - \sqrt{5}$ D、 $\sqrt{5} - 2$

查看试题解析

二、填空题

11. 当 $x =$ 时，分式 $\frac{1}{- 3 + x}$ 无意义.

查看试题解析
12. 用科学记数法表示 $- 0.0000105$ 结果是.

查看试题解析
13. 计算： $\sqrt[3]{- 8}$ = ．

查看试题解析
14. 如图，△ABC中，DE垂直平分AC交AB于E，∠A=30°，∠ACB=80°，则∠BCE= °.

查看试题解析
15. 如图，已知△ABC中，∠ABC=45°，F是高AD和BE 的交点，CD=4，则线段DF的长度为.

查看试题解析
16. 某数的平方根为 $x + 1$ 和 $2 x - 7$ ，则这个数是.

查看试题解析
17. 已知 $a 、 b$ 为两个连续的整数，且 $a < \sqrt{11} < b$ ，则 $a + b$ = .

查看试题解析

三、解答题

18. 解方程：

(1)、 $\frac{x}{x + 1} - \frac{1}{x - 1} = 1$ ；

(2)、 $\frac{3}{x + 2} + \frac{1}{x} = \frac{4}{x^{2} + 2 x}$

查看试题解析
19. 化简：

(1)、 $\frac{- 2}{a - 1} + \frac{a^{2} - 4 a + 4}{a^{2} - 1} \cdot \frac{a + 1}{a - 2}$ ；

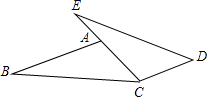
(2)、 $(\frac{3}{x - 2} + \frac{2}{x + 2}) \div \frac{5 x^{2} + 2 x}{x^{2} - 4}$

查看试题解析
20. 已知：如图，点E，A，C在同一条直线上，AB∥CD，AB=CE，AC=CD．
求证：BC=ED．

查看试题解析
21. 如图，已知：点B、F、C、E在一条直线上，FB=CE，AC=DF.能否由上面的已知条件证明AB∥ED？如果能，请给出证明；如果不能，请从下列三个条件中选择一个合适的条件，添加到已知条件中，使AB∥ED成立，并给出证明.

供选择的三个条件（请从其中选择一个）：

①AB=ED；

②BC=EF；

③∠ACB=∠DFE.

查看试题解析
22. 计算：

(1)、 $\sqrt{\frac{1}{16}} - {(- 2)}^{- 2} - {(\sqrt{3} - 2)}^{0}$

(2)、 ${(- 2)}^{2} \times \sqrt{\frac{9}{4}} + | \sqrt[3]{- 8} + \sqrt{3} | + \sqrt{3}$

查看试题解析
23. 已知x的两个平方根分别是 $a + 3$ 和 $2 a - 15$ ，又 $\sqrt[3]{x - y - 2} = 3$ ，求x，y的值.

查看试题解析
24. 在△ABC中，∠ACB＝2∠B，如图①，当∠C＝90°，AD为∠BAC的角平分线时，在AB上截取AE＝AC，连结DE，易证AB＝AC＋CD.

(1)、如图②，当∠C≠90°，AD为∠BAC的角平分线时，线段AB，AC，CD又有怎样的数量关系？不需要证明，请直接写出你的猜想；

(2)、如图③，当AD为△ABC的外角平分线时，线段AB，AC，CD又有怎样的数量关系？请写出你的猜想，并对你的猜想给予证明.

查看试题解析