吉林省松原市乾安县2021-2022学年七年级上学期数学期中试卷

试卷更新日期：2021-11-01 类型：期中考试

进入出卷网下载

一、单项选择题（每小题2分，共12分）

1. 如图，数轴上蚂蚁所在点表示的数可能为（）

A、3 B、0 C、-1 D、-2

查看试题解析
2. 下列说法：①相反数等于它本身的数只有0；②倒数等于它本身的数只有1；③绝对值等于它本身的数只有0；④平方等于它本身的数只有1；其中错误的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 下列各组中，是同类项的是（）

A、-2x²y和xy² B、x²y和x²z C、2mn和4nm D、-ab和abc

查看试题解析
4. 下列概念表述正确的是（）

A、单项式ab的系数是0，次数是2 B、-4a²b，3ab，5是多项式-4a²b+3ab-5的项 C、单项式-2³a³b³的系数是-2，次数是5 D、 $\frac{x y - 1}{2}$ 是二次二项式

查看试题解析
5. 若-xy＜0且y＜0，则2x+5|x|等于（）

A、7x B、-3y C、-3x D、3x

查看试题解析
6. 多项式 $x^{2} - 3 k x y - 3 y^{2} + \frac{1}{3} x y - 8$ 合并同类项后不含xy项，则k的值是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{6}$ C、 $\frac{1}{9}$ D、0

查看试题解析

二、填空题（每小题3分，共24分）

7. 圣湖冬捕，世界奇观，查干湖以26万公斤的惊人数字创下了单网冬捕产量新的吉尼斯世界纪录.将26万用科学记数法可表示为．

查看试题解析
8. 下列各数|﹣2|，﹣（﹣2），（﹣2）² ，（﹣2）³ ， ﹣2²中，负数的个数为个.

查看试题解析
9. 如果一个单项式 $- \frac{a^{2} b}{3}$ 的系数和次数分别为m、n，那么2mn＝.

查看试题解析
10. 已知长方形的周长为4a+2b，其一边长为a﹣b，则另一边长为．

查看试题解析
11. 某商场对原单价为a元的书包打7折出售，则该种书包的现在单价为元．

查看试题解析
12. 当x=3时，代数式px³+qx+1的值为2022，则当x=-3时，代数式px³+qx+1的值是．

查看试题解析
13. 如果定义新运算： $a * b = \frac{a + b}{a - b} (a \neq b)$ ，那么（1※2）※3的值为．

查看试题解析
14. 按一定规律排列的一列数依次为 $- \frac{1}{2} ， \frac{1}{3} ， - \frac{1}{10} ， \frac{1}{15} ， - \frac{1}{26} ， \frac{1}{35} ， \dots \dots$ 按此规律排列下去，这列数中第七个数是.

查看试题解析

三、解答题（每小题5分，共20分）

15. 计算：

(1)、（﹣12）﹣5+（﹣14）﹣（﹣39）

(2)、 $(- 24) \times (\frac{1}{8} - \frac{1}{3} + \frac{1}{4}) + {(- 2)}^{3}$

查看试题解析
16. 先化简，再求值 $(3 x^{2} y - 2 x y^{2}) - (x y^{2} - 2 x^{2} y)$ 其中x=-1，y=2.

查看试题解析
17. 已知下面5个式子：①x²-x+1，②m²n+mn-1，③ $x^{4} + \frac{1}{x} + 2$ ，④5-x² ， ⑤-x² ．回答下列问题：

(1)、上面5个式子中有个多项式，次数最高的多项式为（填序号），整式有个．

(2)、选择2个二次多项式，并进行加法运算．

查看试题解析
18. 如图所示，数轴上一动点A向左移动2个单位长度到达点B，再向右移动5个单位长度到达点C点.

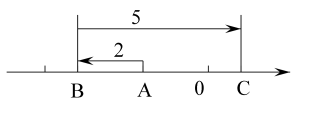(1)、求动点A所走过的路程及A、C之间的距离.

(2)、若C表示的数为1，则点A表示的数为.

查看试题解析

四、解答题（每小题7分，共28分）

19. 如图，将边长为m的正方形纸板，沿虚线剪成两个正方形和两个长方形，拿掉边长为n的小正方形纸板后，将剩下的三个图形拼成一个新的长方形.

(1)、求拼成的新的长方形的周长（用含m或n的代数式表示）；

(2)、当m=7，n=4时，直接写出拼成的新的长方形的面积.

查看试题解析
20. 已知a、b、c三个数在数轴上的位置如图所示，

(1)、判断a、b、c的符号；

(2)、化简 $| a - b | - | b - c | + | c + a | + | b | - 2 | a |$

查看试题解析
21. 为鼓励市民节约用水，特制定如下的收费标准：若每月每户用水不超过10立方米，则按3元/立方米的水价收费，并加收0.2元/立方米的污水处理费；若超过10立方米，则超过的部分按4元/立方米的水价收费，污水处理费不变．

(1)、若小华家5月份的用水量为8立方米，那么小华家5月份的水费为元；

(2)、若小华家6月份的用水量为15立方米，那么小华家6月份的水费为元；

(3)、若小华家某个月的用水量为a（a＞10）立方米，求小华家这个月的水费（用含a的式子表示）

查看试题解析
22. 阅读下面的解题过程：
计算2（﹣4a+3b）﹣3（a﹣2b）．

解：原式=（﹣8a+6b）﹣（3a﹣6b）    （第一步）

=﹣8a+6b﹣3a﹣6b                    （第二步）

=﹣11a+12b                            （第三步）

(1)、这个题，错误的步骤是（   ）

A、三步都错 B、第一步和第二步 C、第一步和第三步 D、第二步和第三步

(2)、请写出正确的解题步骤.

查看试题解析

五、解答题（每小题8分，共16分）

23. 某路公交车从起点经过A、B、C、D站到达终点，一路上下乘客如下表所示.（用正数表示上车的人数，负数表示下车的人数）

	起点	A	B	C	D	终点
上车的人数	18	15	12	7	5	0
下车的人数	0	-3	-4	-10	-11

(1)、求到终点下车还有多少人？

(2)、车行驶在哪两站之间车上的乘客最多？站和站（直接写出站点即可）

(3)、若每人每乘坐一站地需买票1元，问该车这一趟能收入多少钱？写出算式计算.

查看试题解析

24. 已知 $A = 2 x^{2} - \frac{1}{2} + 3 x$ ， $B = x - x^{2} + \frac{1}{2}$
求：

(1)、A-4B；

(2)、4B-A；

(3)、从（1）（2）的计算结果，你能知道A-4B与4B-A之间有什么关系吗？

查看试题解析

六、解答题（每小题10分，共20分）

25. 某农户承包荒山若干亩，投资7800元改造后，种果树2000棵．今年水果总产量为18000千克，此水果在市场上每千克售a元，在果园每千克售b元（b＜a）．该农户将水果拉到市场出售平均每天出售1000千克，需8人帮忙，每人每天付工资25元，农用车运费及其他各项税费平均每天100元．

(1)、分别用a，b表示两种方式出售水果的收入；

(2)、若a=1.3元，b=1.1元，且两种出售水果方式都在相同的时间内售完全部水果，请你通过计算说明选择哪种出售方式较好；

(3)、该农户加强果园管理，力争到明年纯收入达到15000元，而且该农户采用了（2）中较好的出售方式出售，那么纯收入增长率是多少（纯收入=总收入﹣总支出）？

查看试题解析
26. 如图，已知数轴上点A表示的数为8，B是数轴上一点，且AB=14．动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．

(1)、写出数轴上点B表示的数，点P表示的数（用含t的代数式表示）；

(2)、动点Q从点B出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，问点P运动多少秒时追上点Q？

(3)、若点D是数轴上一点，点D表示的数是x，请你探索式子 $| x + 6 | + | x - 8 |$ 是否有最小值？如果有，直接写出最小值；如果没有，说明理由．

查看试题解析