吉林省松原市乾安县2021-2022学年八年级上学期数学期中试卷
试卷更新日期：2021-11-01 类型：期中考试
一、单项选择题（每小题2分，共12分）
-
1. 北京2022年冬奥会会徽“冬梦”已经发布．以下是参选的会徽设计的一部分图形，其中是轴对称图形的是（ ）A、
B、
C、
D、
2. 一个多边形的边数由原来的3增加到n时（n＞3，且n为正整数），它的外角和（ ）A、增加（n-1）×180° B、增加（n-2）×180° C、减小（n-2）×180° D、没有改变3. 若等腰三角形的一边长等于5，另一边长等于3，则它的周长等于（ ）
A、10 B、11 C、13 D、11或134. 如图，是屋架设计图的一部分，点D是斜梁AB的中点，立柱BC、DE垂直于横梁AC，AB=8m，∠A=30°，则DE等于（ ）
A、1m B、2m C、3m D、4m5. 如图，已知AE=CF，∠AFD=∠CEB，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（ ）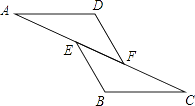
A、∠A=∠C B、AD=CB C、BE=DF D、AD∥BC6. 如图，小敏做了一个角平分仪ABCD，其中AB=AD，BC=DC，将仪器上的A点与∠PRQ的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A，C画一条射线AE，AE就是∠PRQ的平分线．此角平分仪的画图原理是：根据仪器结构，可得△ABC≌△ADC，这样就有∠QAE=∠PAE．则说明这两个三角形全等的依据是（ ）
A、SSS B、ASA C、AAS D、SAS二、填空题（每小题3分，共24分）
-
7. 已知点A（x，－4）与点B（3，y）关于x轴对称，那么x＋y的值为 ．8. 如图，一扇窗户打开后，用窗钩BC将其固定.这里所运用的几何原理是 ．
9. 如图，已知△ABC中，∠A＝40°，剪去∠A后变成四边形，则∠1＋∠2＝°。
10. 如图，Rt△ABC和Rt△EDF中，∠B＝∠D，在不添加任何辅助线的情况下，请你添加一个条件 ， 使得Rt△ABC≌Rt△EDF.
11. 如图，AD，CE分别是△ABC的中线和角平分线．若AB=AC，∠CAD=20°，则∠ACE的度数是.
12. 如图，DE是△ABC中AC边的垂直平分线，若BC=8，AB=10，则△EBC的周长是.
13. 如图，等边三角形纸片ABC的边长为6，E、F是边BC上的三等分点.分别过点E、F沿着平行于BA、CA方向各剪一刀，则剪下的△DEF的周长是.
14. 如图，D为等腰Rt△ABC的斜边AB的中点，E为BC边上一点，连接ED并延长交CA的延长线于点F，过D作DH⊥EF交AC于G，交BC的延长线于H，则以下结论：①BE=CG；②DF=DH；③BH=CF；④AF=CH．其中正确的是.
三、解答题（每小题5分，共20分）
-
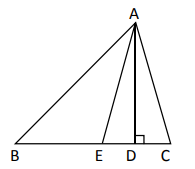
15. 一个多边形的内角和是它的外角和的4倍，求这个多边形的边数和对角线条数．16. 如图，在△ABC中，AD是BC边上的高，AE是∠BAC的平分线，∠B=42°，∠DAE=18°，求∠C的度数．
17. 如图所示，D是边AB的中点，△BCD的周长比△ACD的周长大3cm，BC＝8cm，求边AC的长.
18. 如图，△ABC与△DCB中，AC与BD交于点E，且∠A=∠D，AB=DC．求证：△ABE≌△DCE.
四、解答题（每小题7分，共28分）
-
19. 如图，在平面直角坐标系中，A（1，2）、B（3，1）、C（-2，-1）．
(1)、在图中作出△ABC关于y轴对称的△A1B1C1；(2)、写出A1、B1、C1的坐标；(3)、求△A1B1C1的面积．20. 如图，在△ABC中，∠C=90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB于点E．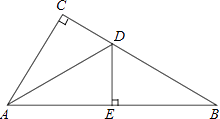
(1)、求证：△ACD≌△AED；(2)、若∠B=30°，CD=1，求BD的长．21. 已知a、b、c是△ABC的三边长，a=4，b=6，设三角形的周长是x．(1)、直接写出c及x的取值范围；(2)、若x是小于18的偶数，①求c的长；②判断△ABC的形状．
22. 如图，已知OC是∠AOB的平分线，将直尺DEMN如图摆放，使EM边与OB边重合，顶点D落在OA边上，DN边与OC交于点P.
(1)、猜想△DOP是三角形.(2)、证明你的猜想，写出解答过程.五、解答题（每小题8分，共16分）
-
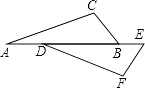
23. 已知命题：如图，点A，D，B，E在同一条直线上，且AD=BE，∠A=∠FDE，则△ABC≌△DEF．判断这个命题是真命题还是假命题，如果是真命题，请给出证明；如果是假命题，请添加一个适当条件使它成为真命题，并加以证明．
24. 如图1，在四边形ABCD中，DC∥AB，AD=BC，BD平分∠ABC．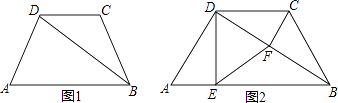
(1)、求证：AD=DC；(2)、如图2，在上述条件下，若∠A=∠ABC=60°，过点D作DE⊥AB，过点C作CF⊥BD，垂足分别为E、F，连接EF．判断△DEF的形状并证明你的结论．六、解答题（每小题10分，共20分）
-
25. 如图，在平面直角坐标系中，直线l是第一、三象限的角平分线．
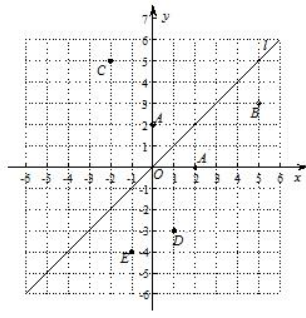(1)、实验与探究：
由图观察易知A（0，2）关于直线l的对称点A′的坐标为（2，0），请在图中分别标明B(5，3)、C(-2，5)关于直线l的对称点B′、C′的位置，并写出他们的坐标：B′、C′；(2)、归纳与发现：
结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点P(a，b)关于第一、三象限的角平分线l的对称点P′的坐标为（不必证明）；(3)、运用与发现：
已知两点D(1，-3)、E(-1，-4)，试在直线l上确定一点Q，使点Q到D、E两点的距离之和最小.26. 如图（1），AB＝4cm，AC⊥AB，BD⊥AB，AC＝BD＝3cm．点P在线段AB上以1cm/s的速度由点A向点B运动，同时，点Q在线段BD上由点B向点D运动．它们运动的时间为t（s）．
(1)、若点Q的运动速度与点P的运动速度相等，当t＝1时，△ACP与△BPQ是否全等，请说明理由，并判断此时线段PC和线段PQ的关系；(2)、如图（2），将图（1）中的“AC⊥AB，BD⊥AB”为改“∠CAB＝∠DBA＝60°”，其他条件不变．设点Q的运动速度为xcm/s，是否存在实数x，使得△ACP与△BPQ全等？若存在，求出相应的x、t的值；若不存在，请说明理由.