山东省济宁市梁山县2021-2022学年九年级上学期数学10月月考试卷

试卷更新日期：2021-11-01 类型：月考试卷

进入出卷网下载

一、选择题：本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项符合题目要求。

1. 下列方程是一元二次方程的是（）

A、2x-3y+1 B、3x+y=z C、x²-5x=1 D、x²- $\frac{1}{x}$ +2=0

查看试题解析
2. 一元二次方程x²-2x+1=0的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断

查看试题解析
3. 一元二次方程x（3x+2）= 6（3x+2）的解是（）

A、x=6 B、x= $- \frac{2}{3}$ C、x₁=6，x₂= $- \frac{2}{3}$ D、x₁=-6，x₂= $\frac{2}{3}$

查看试题解析
4. 已知x=1是关于x的一元二次方程（m-2）x²+m²=4的根，则m的值为（）

A、2 B、-2或3 C、2或-3 D、-3

查看试题解析
5. 若实数a，b（a不等b）分别满足方程a²-7a+2=0，b²-7b+2=0，则 $\frac{b}{a} + \frac{a}{b}$ 的值为（）

A、 $\frac{45}{2}$ B、 $\frac{49}{2}$ C、 $\frac{45}{2}$ 或2 D、 $\frac{49}{2}$ 或2

查看试题解析
6. 关于方程x²+2x- 4=0的根的情况，下列结论错误的是（）

A、有两个不相等的实数根 B、两实数根的和为2 C、两实数根的差为± $2 \sqrt{5}$ D、两实数根的积为-4

查看试题解析
7. 若m，n为方程x²-3x-1=0的两根，则多项式m²+3n的值为（）

A、-8 B、-9 C、9 D、10

查看试题解析
8. 某校为落实“光盘行动”，对每天的剩饭菜进行称重，第一周的剩余量为20kg，第三周为9.8kg，设每周剩余量的平均减少率为x，则可列方程（）

A、20（1-x）²=9.8 B、20（1+x）²=9.8 C、20（1-2x）=9.8 D、20（1+2x）=9.8

查看试题解析
9. 要使关于x的一元二次方程ax²+2x-1=0有两个实数根，且使关于x的分式方程 $\frac{x}{x - 4} + \frac{a + 2}{4 - x}$ =2的解为非负数的所有整数a的个数为（）

A、5个 B、6个 C、7个 D、8个

查看试题解析
10. 下列函数中，当x>0时，y值随x值增大而减小的函数有（）
⑴y=2x²；（2）y= $- \frac{1}{2}$ x²；（3）y=-2x；（4）y=3x；（5）y=-3x-2；

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题：（本大题共6个小题，每小题3分，共18分） 261821 2w0

11. 关于x的方程（a+1）x^a2+1+x-5=0是一元二次方程，则a=

查看试题解析
12. 把一元二次方程x²+6x-1=0通过配方化成（x+m）²=n的形式为

查看试题解析
13. 已知三角形两边长分别是2和9，第三边的长为一元二次方程x²-14x+48=0的一个根，则这个三角形的周长为

查看试题解析
14. 如图，要设计一副宽20cm、长30cm的图案，其中有两横两竖的彩条，横、竖彩条的宽度比为2：3，如果要使彩条所占面积是图案面积的 $\frac{9}{25}$ ，则每个横彩条的宽度是cm

查看试题解析
15. 如图，抛物线y=ax²-4和y=-ax²+4都经过x轴上的A、B两点，两条抛物线的顶点分别为C、D.当四边形ACBD的面积为40时，a的值为

查看试题解析
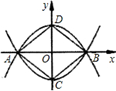16. 如图，B是AC上一点，且BC=6cm，AB=4cm，射线BD⊥AC，垂足为B，动点M从A出发以2cm/s的速度沿着AC向C运动，同时动点N从B出发以3cm/s的速度沿着射线BD向下运动，连接MN。当△BMN的面积为 $\frac{3}{2}$ cm² ，两动点运动了t（s），则t的值为。

查看试题解析

三、解答题（本大题共6个小题，共52分）

17. 用适当的方法解下列方程：（每题3分，共12分）

(1)、4x（2x+3）=8（2x+3）

(2)、x²-2x-5=0

(3)、3x²+x-5=0

(4)、x²+6（x+1）-13=0

查看试题解析
18. 已知关于x的一元二次方程x²-2（m-1）x+m²=0有实数根．

(1)、求m的取值范围；

(2)、设此方程的两个根分别为x₁ ， x₂ ，若x₁²+x₂²=8-3x₁x₂ ，求m的值

查看试题解析
19. 已知关于x的一元二次方程ax²+bx+ $\frac{1}{2}$ =0

(1)、若x=1是方程的一个解，写出a、b满足的关系式；

(2)、当b=a+1时，利用根的判别式判断方程根的情况．

查看试题解析
20. 某商店销售某种商品，平均每天可售出20件，每件盈利40元，为了扩大销售，增加盈利，该店采取了降价措施，在每件盈利不少于25元的前提下，经过一段时间销售，发现销售单价每降低1元，平均每天可多售出2件。

(1)、若降价6元时，则平均每天销售数量为多少件？

(2)、当每件商品降价多少元时，该商店每天销售利润为1200 元？

查看试题解析
21. 已如x关于的方程：x²-（2k+1）x+（k- $\frac{1}{2}$ ）=0

(1)、若x=1是这个方程的一个根，求k的值和它的另一个根。

(2)、若等腰△ABC的一边长a=4，另两边b、C恰好是这个方程的两个根，求这个等腰三角形的周长是多少？

查看试题解析
22. 如图，在菱形ABCD中，m、n、t分别是菱形ABCD的两条对角线长和边长，这时我们把关于x的形如“mx²+2 $\sqrt{2}$ tx+n=0”的元二次方程称为“菱系一元二次方程”。请解决下列问题：

(1)、填空：
①当m=6，n=8时，t=

②用含m，n的代数式表示t²值，t²=

(2)、求证：关于x的“菱系一元二次方程” mx²+2 $\sqrt{2}$ tx+n=0必有实数根：

(3)、若x=-1是“菱系一元二次方程”mx²+2 $\sqrt{2}$ tx+n=0的一个根，且菱形的面积是25，BE是菱形ABCD的AD边上的高，求BE的值。

查看试题解析