山东省济宁市梁山县2021-2022学年八年级上学期数学10月月考试卷
试卷更新日期:2021-11-01 类型:月考试卷
一、选择题:本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项符合题目要水。
-
1. 下列四个图中,正确画出△ABC中BC边上的高是( )A、
 B、
B、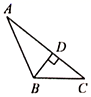 C、
C、 D、
D、 2. 根据下列已知条件,能作出唯一△ABC的是( )A、AB=3,BC=4,CA=8 B、AB=4,BC=3,∠A=60° C、∠A=60°,∠B=45°,AB=4 D、∠C=90°,∠B=30°,∠A=60°3. 如图,△ABC≌△ADE,若∠BAE=120,∠BAD=40°,则∠BAC的度数为( )
2. 根据下列已知条件,能作出唯一△ABC的是( )A、AB=3,BC=4,CA=8 B、AB=4,BC=3,∠A=60° C、∠A=60°,∠B=45°,AB=4 D、∠C=90°,∠B=30°,∠A=60°3. 如图,△ABC≌△ADE,若∠BAE=120,∠BAD=40°,则∠BAC的度数为( ) A、40° B、80° C、120° D、100°4. 如图所示的五边形木架不具有稳定性,若要使该木架稳定,则要钉上的细木条的数量至少为( )
A、40° B、80° C、120° D、100°4. 如图所示的五边形木架不具有稳定性,若要使该木架稳定,则要钉上的细木条的数量至少为( ) A、1 B、2 C、3 D、45. 如图,已知AB=AC,AD=AE,欲证△ABD≌△ACE,不可补充的条件是( )
A、1 B、2 C、3 D、45. 如图,已知AB=AC,AD=AE,欲证△ABD≌△ACE,不可补充的条件是( ) A、BD=CE B、∠1=∠2 C、∠BAD=∠CAE D、∠D=∠E6. 下列多边形中,不能够单独铺满地面的是( )A、正三角形 B、正方形 C、正五边形 D、正六边形7. 把一张形状是多边形的纸片剪去其中某一个角,剩下的部分是一个四边形,则这张纸片原来的形状不可能是( )A、三角形 B、四边形 C、五边形 D、六边形8. 如图,在△ABC中,AB=AC,AE是经过点A的一条直线,且B,C在AE的两侧,BD⊥AE于D,CE⊥AE于E,AD=CE,则∠BAC的度数是( )
A、BD=CE B、∠1=∠2 C、∠BAD=∠CAE D、∠D=∠E6. 下列多边形中,不能够单独铺满地面的是( )A、正三角形 B、正方形 C、正五边形 D、正六边形7. 把一张形状是多边形的纸片剪去其中某一个角,剩下的部分是一个四边形,则这张纸片原来的形状不可能是( )A、三角形 B、四边形 C、五边形 D、六边形8. 如图,在△ABC中,AB=AC,AE是经过点A的一条直线,且B,C在AE的两侧,BD⊥AE于D,CE⊥AE于E,AD=CE,则∠BAC的度数是( ) A、45° B、60° C、90° D、120°9. 如图,在四边形ABCD中,∠ABC与∠BCD的平分线的交点E恰好在AD边上,则∠BEC=( )
A、45° B、60° C、90° D、120°9. 如图,在四边形ABCD中,∠ABC与∠BCD的平分线的交点E恰好在AD边上,则∠BEC=( ) A、∠A+∠D-45° B、 (∠A+∠D) +45° C、180°-(∠A+∠D) D、 ∠A+ ∠D10. 如图在△ABC中,BO,CO分别平分∠ABC,∠ACB,交于O,CE为外角∠ACD的平分线,BO的延长线交CE于点E,记∠BAC=∠1,∠BEC=∠2,则以下结论①∠1=2∠2,②∠BOC=3∠2,③∠BOC=90°+∠1,④∠BOC=90°+∠2正确的是( )
A、∠A+∠D-45° B、 (∠A+∠D) +45° C、180°-(∠A+∠D) D、 ∠A+ ∠D10. 如图在△ABC中,BO,CO分别平分∠ABC,∠ACB,交于O,CE为外角∠ACD的平分线,BO的延长线交CE于点E,记∠BAC=∠1,∠BEC=∠2,则以下结论①∠1=2∠2,②∠BOC=3∠2,③∠BOC=90°+∠1,④∠BOC=90°+∠2正确的是( ) A、①②③ B、①③④ C、①④ D、①②④
A、①②③ B、①③④ C、①④ D、①②④二、填空题:本大题共6小题,每小题3分,共18分.
-
11. 如图,在△ABC中,点D,E,F分别为BC,AD,CE的中点,且S△BEF=2cm2 , 则S△ABC= cm2
 12. 三个数3, 1-a,1-2a在数轴上从左到右依次排列,且以这三个数为边长能构成三角形,则a的取值范围为13. 如图,∠A+∠B+∠C+∠D+∠E=.
12. 三个数3, 1-a,1-2a在数轴上从左到右依次排列,且以这三个数为边长能构成三角形,则a的取值范围为13. 如图,∠A+∠B+∠C+∠D+∠E=. 14. “过点P作直线b,使b∥a",小明的作图痕迹如图所示,他的作法的依据是
14. “过点P作直线b,使b∥a",小明的作图痕迹如图所示,他的作法的依据是 15. 如图,正方形ABCD的顶点A在直线l上,BE上直线l于点E,连接DE,若AE=3,则△ADE的面积为
15. 如图,正方形ABCD的顶点A在直线l上,BE上直线l于点E,连接DE,若AE=3,则△ADE的面积为 16. 如图, , ,且 ,则 .
16. 如图, , ,且 ,则 .
三、解答题(本大题共6个小题,共52分)
-
17. 如图,在Rt△ABC中,∠ACB=90°
 (1)、作∠BAC的平分线交BC于点D (不写作法,保留作图痕迹).(2)、在(1)的条件下,若CD=3,AB=10,则△ABD的面积为18. 如图,已知,在△ABC中,∠B<∠C,AD平分∠BAC,点E是线段AD (除去端点A、D)上一动点,EF⊥BC于点F。
(1)、作∠BAC的平分线交BC于点D (不写作法,保留作图痕迹).(2)、在(1)的条件下,若CD=3,AB=10,则△ABD的面积为18. 如图,已知,在△ABC中,∠B<∠C,AD平分∠BAC,点E是线段AD (除去端点A、D)上一动点,EF⊥BC于点F。 (1)、若∠B=40°,∠DEF=10°,求∠C的度数。(2)、若∠B=α,∠C=β,请用含α、β的式子表示∠DEF的度数。19. 如图,点M、N分别是正八边形ABCDEFGH (每条边相等,每个角相等)的边BC、CD上的点,且BM=CN,AM交BN于点P。
(1)、若∠B=40°,∠DEF=10°,求∠C的度数。(2)、若∠B=α,∠C=β,请用含α、β的式子表示∠DEF的度数。19. 如图,点M、N分别是正八边形ABCDEFGH (每条边相等,每个角相等)的边BC、CD上的点,且BM=CN,AM交BN于点P。 (1)、求证:△ABM≌△BCN:(2)、求∠APN的度数。20. 小明在求一个凸n边形的内角和时,没有把其中一个角的度数算进去,求得的内角和为2570°(1)、求这个多边形的边数(2)、没有算进去的那个内角为多少度?21. 如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)、求证:△ABM≌△BCN:(2)、求∠APN的度数。20. 小明在求一个凸n边形的内角和时,没有把其中一个角的度数算进去,求得的内角和为2570°(1)、求这个多边形的边数(2)、没有算进去的那个内角为多少度?21. 如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.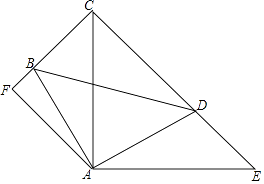 (1)、求证:△ABC≌△ADE;
(1)、求证:△ABC≌△ADE;
(2)、求∠FAE的度数;(3)、求证:CD=2BF+DE.22. (问题背景)在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,试探究图1中线段BE、EF、FD之间的数量关系。
 (1)、(初步探索)
(1)、(初步探索)小晨同学认为:延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,则可得到BE、EF 、FD之间的数量关系是
(2)、(探索延伸)在四边形ABCD中如图2,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的
点,∠EAF= ∠BAD,上述结论是否仍然成立?说明理由。
(3)、(结论运用)如图3,在某次南海海域军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以80海里/小时的速度前进,舰艇乙沿北偏东50°的方向以100海里/小时的速度前进1.2小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角(∠EOF)为70°,试求此时两舰艇之间的距离。