上海市松江区2021-2022学年九年级上学期数学第一次月考试卷
试卷更新日期:2021-11-01 类型:月考试卷
一、单选题
-
1. 下列图形中不一定是相似图形的是( )A、两个等边三角形 B、两个顶角相等的等腰三角形 C、两个等腰直角三角形 D、两个矩形2. 如图,已知AB∥CD,AD与CD相交于点O,AO:DO=1:2,则下列式子错误的为( )
 A、 B、 C、 D、3. 如图,△ABC中,D、E分别在△ABC的边AB、AC的反向延长线上,下面比例式中,不一定能判断ED∥BC的是( )
A、 B、 C、 D、3. 如图,△ABC中,D、E分别在△ABC的边AB、AC的反向延长线上,下面比例式中,不一定能判断ED∥BC的是( ) A、 B、 C、 D、4. 已知线段a、b、c,作线段x,使 ,则正确的作法是( )A、
A、 B、 C、 D、4. 已知线段a、b、c,作线段x,使 ,则正确的作法是( )A、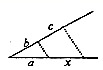 B、
B、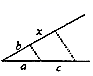 C、
C、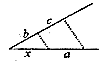 D、
D、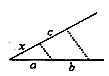 5. 已知非零向量 , , ,下列条件中,不能判定 的是( )A、 ; B、 ; C、 , ; D、 , .6. 如图,△ABC中,D、E两点分别在BC、AC上,且AD平分∠BAC,若∠ABE=∠C,BE与AD相交于点F.则图中相似三角形的对数是( )
5. 已知非零向量 , , ,下列条件中,不能判定 的是( )A、 ; B、 ; C、 , ; D、 , .6. 如图,△ABC中,D、E两点分别在BC、AC上,且AD平分∠BAC,若∠ABE=∠C,BE与AD相交于点F.则图中相似三角形的对数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
7. 在比例尺为1﹕50000的地图上量出A、B两地的距离是12cm,那么A、B两地的实际距离是 千米.8. 若线段b是线段a和c的比例中项,且a=1cm,c=9cm,则b=cm.9. 已知点P是线段AB上的一个黄金分割点,且AB=10cm,AP>BP,那么AP=cm10. 在△ABC中,点D、E分别在边AB、AC上,且DE∥BC,AB=12cm,AE=11cm,CE=4cm,那么DB=cm.11. 某同学的身高为1.6米,某一时刻他在阳光下的影长为1.2米,与他相邻的一棵树的影长为3.6米,则这棵树的高度为米.12. 已知点G是△ABC的重心,AG=4,那么点G与边BC中点之间的距离是 .13. 如图,l1∥l2∥l3 , AB= AC,DF=10,那么DE=.
 14. 已知△ABC与ΔA'B'C'相似,并且点A与点A'、点B与点B'、点C与点C'是对应顶点,其中∠A=80°,∠B'=60°,则∠C=度.15. 两个相似三角形的对应中线的比为 ,那么它们的周长比是.16. 已知向量 与单位向量 方向相反,且 ,那么 =(用向量 的式子表示)17. 如图,△ABC中,BC=12,点D、E分别在边AB、AC上,DE//BC,且S△ADE=S四边形DBCE , 则DE= .
14. 已知△ABC与ΔA'B'C'相似,并且点A与点A'、点B与点B'、点C与点C'是对应顶点,其中∠A=80°,∠B'=60°,则∠C=度.15. 两个相似三角形的对应中线的比为 ,那么它们的周长比是.16. 已知向量 与单位向量 方向相反,且 ,那么 =(用向量 的式子表示)17. 如图,△ABC中,BC=12,点D、E分别在边AB、AC上,DE//BC,且S△ADE=S四边形DBCE , 则DE= . 18. 已知:△ABC∽△DEF,且∠A=∠D,AB=8,AC=6,DE=2,那么DF= .
18. 已知:△ABC∽△DEF,且∠A=∠D,AB=8,AC=6,DE=2,那么DF= .三、解答题
-
19. 已知 ≠0,求 的值.20. 已知:如图,在梯形ABCD中,AD∥MN∥BC.MN分别交边AB、DC于点M、N.如果AM:MB=2:3,AD=2,BC=7.求MN的长.
 21. 如图,在平行四边形ABCD中,点E为边BC上一点,连接AE并延长AE交DC的延长线于点M,交BD于点G,过点G作GF∥BC交DC于点F.
21. 如图,在平行四边形ABCD中,点E为边BC上一点,连接AE并延长AE交DC的延长线于点M,交BD于点G,过点G作GF∥BC交DC于点F.求证: .
 22. 如图,AD和BC相交于点E,AC∥BD,点F在CD上,AC=4,BD=6, ,
22. 如图,AD和BC相交于点E,AC∥BD,点F在CD上,AC=4,BD=6, ,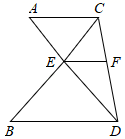 (1)、求EF的长;(2)、已知S△CBD=25,求△CEF的面积.23. 如图,D、E是△ABC边AB上的点,F、G分别是边AC、BC上的点,且满足AD=DE=EB,DF∥BC,GE∥AC.
(1)、求EF的长;(2)、已知S△CBD=25,求△CEF的面积.23. 如图,D、E是△ABC边AB上的点,F、G分别是边AC、BC上的点,且满足AD=DE=EB,DF∥BC,GE∥AC. (1)、求证:FG∥AB;(2)、设 = , = ,请用向量 , 表示 .
(1)、求证:FG∥AB;(2)、设 = , = ,请用向量 , 表示 .

