山东省青岛三十九中2021-2022学年九年级上学期数学第一次月考试卷
试卷更新日期:2021-11-01 类型:月考试卷
一、单选题
-
1. 下列方程是一元二次方程的是( )A、(x2+3)2=9 B、ax2+bx+c=0 C、x2+3=0 D、x2+ =42. 一元二次方程 的根的情况是( )A、有一个实数根 B、没有实数根 C、有两个相等的实数根 D、有两个不相等的实数根3. 观察下列表格,估计一元二次方程x2+3x-5=0的正数解在( )
x
-1
0
1
2
3
4
x2+3x-5
-7
-5
-1
5
13
23
A、-1和0之间 B、0和1之间 C、1和2之间 D、2和3之间4. 下列命题中,真命题是( )A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是菱形 C、对角线互相平分的四边形不一定是平行四边形 D、对角线互相垂直平分且相等的四边形一定是正方形5. 在一个四边形ABCD中依次连接各边的中点得到的四边形是矩形,则对角线AC与BD需要满足的条件是( )A、垂直 B、相等 C、垂直且相等 D、不再需要条件6. 已知已知 、 是一元二次方程 的两根,则 的值是( )A、 B、 C、 D、7. 如图,在三角形ABC中,AB=AC,BC=6,三角形DEF的周长是7,AF⊥BC于F,BE⊥AC于E,且点D是AB的中点,则AF=( )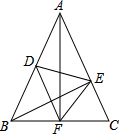 A、 B、 C、 D、78. 如图,在矩形ABCD中,O为AC中点, 交AB于E,点G是AE中点且∠AOG=30°,下列结论:(1)DC=3OG;(2)OG= BC;(3) 等边三角形;(4)S△AOE= S矩形ABCD , 正确的有( )
A、 B、 C、 D、78. 如图,在矩形ABCD中,O为AC中点, 交AB于E,点G是AE中点且∠AOG=30°,下列结论:(1)DC=3OG;(2)OG= BC;(3) 等边三角形;(4)S△AOE= S矩形ABCD , 正确的有( )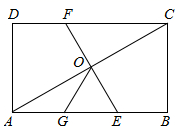 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 方程x2=x的解为 .10. 若a是方程x2+x﹣1=0的根,则代数式2022﹣3a2﹣3a的值是 .11. 某工厂一月份生产机器100台,计划二、三月份共生产机器250台,设二、三月份的平均增长率为x,则根据题意列出方程是 .12. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,S菱形ABCD=48,则OH的长为 .
 13. 小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得 ,接着活动学具成为图2所示正方形,并测得正方形的对角线 ,则图1中对角线AC的长为 .
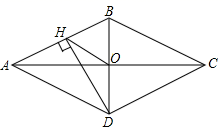
13. 小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得 ,接着活动学具成为图2所示正方形,并测得正方形的对角线 ,则图1中对角线AC的长为 .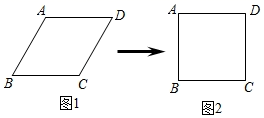 14. 如图,在矩形ABCD中,AC、BD相交于点O,AE平分∠BAD,交BC于B,已知∠EAO=15°,AC=6,那么△BOE的面积为 .
14. 如图,在矩形ABCD中,AC、BD相交于点O,AE平分∠BAD,交BC于B,已知∠EAO=15°,AC=6,那么△BOE的面积为 . 15. 关于x的一元二次方程(a+1)x2-2x+3=0有实数根,则整数a的最大值是.16. 如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为 .
15. 关于x的一元二次方程(a+1)x2-2x+3=0有实数根,则整数a的最大值是.16. 如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为 .
三、解答题
-
17. 尺规作图
在三角形内做一个最大的菱形,使A为菱形的一个内角.
 18. 解方程.(1)、x2﹣2x﹣4=0(用配方法);(2)、2x2+3x﹣1=0(用公式法);(3)、3x+6=(x+2)2;(4)、9(x+1)2=4(2x﹣1)2 .19. 已知关于x的一元二次方程 有两个不相等的实数根.(1)、求k的取值范围;(2)、若方程的两个不相等实数根是a,b,求 的值.20. 如图,用长为22米的篱笆,一面利用墙(墙的最大可用长度为14米),围成中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在BC上用其他材料做了宽为1米的两扇小门.
18. 解方程.(1)、x2﹣2x﹣4=0(用配方法);(2)、2x2+3x﹣1=0(用公式法);(3)、3x+6=(x+2)2;(4)、9(x+1)2=4(2x﹣1)2 .19. 已知关于x的一元二次方程 有两个不相等的实数根.(1)、求k的取值范围;(2)、若方程的两个不相等实数根是a,b,求 的值.20. 如图,用长为22米的篱笆,一面利用墙(墙的最大可用长度为14米),围成中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在BC上用其他材料做了宽为1米的两扇小门.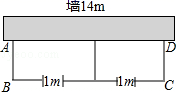 (1)、设花圃的一边AB长为x米,请你用含x的代数式表示另一边AD的长为米;(2)、若此时花圃的面积刚好为45m2 , 求此时花圃的长与宽.21. 某商店经销甲、乙两种商品. 现有如下信息:
(1)、设花圃的一边AB长为x米,请你用含x的代数式表示另一边AD的长为米;(2)、若此时花圃的面积刚好为45m2 , 求此时花圃的长与宽.21. 某商店经销甲、乙两种商品. 现有如下信息:
请根据以上信息,解答下列问题:
(1)、甲、乙两种商品的零售单价分别为元和元.(直接写出答案)(2)、该商店平均每天卖出甲商品500件和乙商品1200件.经调查发现,甲种商品零售单价每降0.1元,甲种商品每天可多销售100件.为了使每天获取更大的利润,商店决定把甲种商品的零售单价下降m(m>0)元.在不考虑其他因素的条件下,当m定为多少时,才能使商店每天销售甲、乙两种商品获取的利润共1700元?22. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且DE= AC,连接CE、OE,连接AE交OD于点F.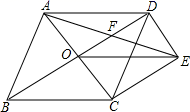 (1)、求证:OE=CD;(2)、若菱形ABCD的边长为8,∠ABC=60°,求AE的长.23. 定义:有一组对角是直角的四边形叫做“准矩形”;有两组邻边(不重复)相等的四边形叫做“准菱形”.如图①,在四边形ABCD中,若∠A=∠C=90°,则四边形ABCD是“准矩形”;如图②,在四边形ABCD中,若AB=AD,BC=DC,则四边形ABCD是“准菱形”.
(1)、求证:OE=CD;(2)、若菱形ABCD的边长为8,∠ABC=60°,求AE的长.23. 定义:有一组对角是直角的四边形叫做“准矩形”;有两组邻边(不重复)相等的四边形叫做“准菱形”.如图①,在四边形ABCD中,若∠A=∠C=90°,则四边形ABCD是“准矩形”;如图②,在四边形ABCD中,若AB=AD,BC=DC,则四边形ABCD是“准菱形”. (1)、如图,在边长为1的正方形网格中,A、B、C在格点(小正方形的顶点)上,请分别在图③、图④中画出“准矩形”ABCD和“准菱形”ABCD′.(要求:D、D′在格点上);
(1)、如图,在边长为1的正方形网格中,A、B、C在格点(小正方形的顶点)上,请分别在图③、图④中画出“准矩形”ABCD和“准菱形”ABCD′.(要求:D、D′在格点上); (2)、下列说法正确的有;(填写所有符合题意结论的序号)
(2)、下列说法正确的有;(填写所有符合题意结论的序号)①一组对边平行的“准矩形”是矩形;②一组对边相等的“准矩形”是矩形;
③一组对边相等的“准菱形”是菱形;④一组对边平行的“准菱形”是菱形.
(3)、如图⑤,在△ABC中,∠ABC=90°,以AC为一边向外作“准菱形”ACEF,且AC=EC,AF=EF,AE、CF交于点D.①若∠ACE=∠AFE,求证:“准菱形”ACEF是菱形;
②在①的条件下,连接BD,若BD=
 ,∠ACB=15°,∠ACD=30°,请直接写出四边形ACEF的面积.
,∠ACB=15°,∠ACD=30°,请直接写出四边形ACEF的面积.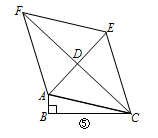 24. 如图,平面直角坐标系中,直线l分别交x轴、y轴于A、B两点(OA<OB)且OA、OB的长分别是一元二次方程 的两个根,点C在x轴负半轴上,
24. 如图,平面直角坐标系中,直线l分别交x轴、y轴于A、B两点(OA<OB)且OA、OB的长分别是一元二次方程 的两个根,点C在x轴负半轴上,且AB:AC=1:2
 (1)、求A、C两点的坐标;(2)、若点M从C点出发,以每秒1个单位的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,写出S关于t的函数关系式,并写出自变量的取值范围;(3)、点P是y轴上的点,在坐标平面内是否存在点Q,使以 A、B、P、Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,请说明理由.
(1)、求A、C两点的坐标;(2)、若点M从C点出发,以每秒1个单位的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,写出S关于t的函数关系式,并写出自变量的取值范围;(3)、点P是y轴上的点,在坐标平面内是否存在点Q,使以 A、B、P、Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,请说明理由.