内蒙古自治区呼和浩特市2021-2022学年九年级上学期数学10月月考试卷
试卷更新日期:2021-11-01 类型:月考试卷
一、单选题
-
1. 方程 的二次项系数和一次项系数分别为( )A、3和-2 B、2和-3 C、2和3 D、-3和22. 二次函数 的图像一定经过( )A、第一、二象限 B、第三、四象限 C、第一、三象限 D、第二、四象限3. 若关于x的一元二次方程(a+1)x2+x+a2-1=0的一个解是x=0,则a的值为( )A、1 B、-1 C、±1 D、04. 用配方法解方程 时,方程可变形为( )A、 B、 C、 D、5. 若抛物线y=﹣7(x+4)2﹣1平移得到y=﹣7x2 , 则必须( )A、先向左平移4个单位,再向下平移1个单位 B、先向右平移4个单位,再向上平移1个单位 C、先向左平移1个单位,再向下平移4个单位 D、先向右平移1个单位,再向上平移4个单位6. 若一元二次方程x2﹣(2m+3)x+m2=0有两个不相等的实数根x1 , x2 , 且x1+x2=x1x2 , 则m的值是( )A、﹣1 B、3 C、3或﹣1 D、﹣3或17. 抛物线y=ax²+bx+c(a>0)与直线y=bx+c在同一坐标系中的大致图像可能为( )A、
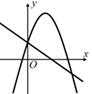 B、
B、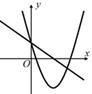 C、
C、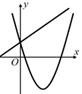 D、
D、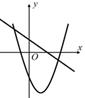 8. 某超市1月份营业额为90万元,1月、2月、3月总营业额为144万元,设平均每月营业额增长率为x , 则下面所列方程正确的是( )A、90(1+x)2=144 B、90(1-x)2=144 C、90(1+2x)=144 D、90(1+x)+90(1+x)2=144-909. 二次函数 的图象如图所示,有如下结论:① ;② ;③ ;④ (m为实数).其中正确结论的个数是( )
8. 某超市1月份营业额为90万元,1月、2月、3月总营业额为144万元,设平均每月营业额增长率为x , 则下面所列方程正确的是( )A、90(1+x)2=144 B、90(1-x)2=144 C、90(1+2x)=144 D、90(1+x)+90(1+x)2=144-909. 二次函数 的图象如图所示,有如下结论:① ;② ;③ ;④ (m为实数).其中正确结论的个数是( )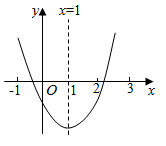 A、1个 B、2个 C、3个 D、4个10. 如图①,正方形 中, , 相交于点O,E是 的中点,动点P从点E出发,沿着 的路径以每秒1个单位长度的速度运动到点A,在此过程中线段 的长度 随着运动时间x的函数关系如图②所示,则 的长为( )
A、1个 B、2个 C、3个 D、4个10. 如图①,正方形 中, , 相交于点O,E是 的中点,动点P从点E出发,沿着 的路径以每秒1个单位长度的速度运动到点A,在此过程中线段 的长度 随着运动时间x的函数关系如图②所示,则 的长为( ) A、 B、4 C、 D、
A、 B、4 C、 D、二、填空题
-
11. 已知 是关于 的一元二次方程,则 .12. 将二次函数y=x2﹣2x﹣3的图象向左平移2个单位长,再向上平移1个单位长,所得的抛物线的解析式为 .13. 关于x的方程2kx2+3x+1=0有两实根,则k的取值范围 .14. 若函数y=(m﹣1)x2﹣6x m的图象与x轴有且只有一个交点,则m的值为 .15. 如果x2﹣x﹣1=(x+1)0 , 那么x的值为 .16. 已知二次函数y=x2﹣3x+m的图象与坐标轴有且只有两个交点,这两个交点坐标是 .
三、解答题
-
17. 用适当的方法解下列方程(1)、2x(x﹣3)=3﹣x;(2)、(x+1)(x﹣2)=1;(3)、(3x﹣2)2=4(x+1)2 .18. 关于x的一元二次方程x2+(2k﹣1)x+k2=0有两个不等实根x1 , x2 ,(1)、求实数k的取值范围;(2)、若方程两实根x1 , x2满足x1+x2+x1x2﹣1=0,求k的值.19. 二次函数y=ax2+bx+c的图象如图所示,根据图象直接回答下列问题:
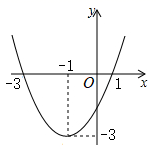 (1)、直接写出该二次函数的解析式为;(2)、不等式ax2+bx+c≤0的解集是;(3)、y随x的增大而减小的自变量x的取值范围是;(4)、若关于x的方程ax2+bx+c=k有两个不相等的实根,则k的取值范围是 .20. 2020年3月,新冠肺炎疫情在中国已经得到有效控制,但在全球却开始持续蔓延,这是对人类的考验,将对全球造成巨大影响.新冠肺炎具有人传人的特性,若一人携带病毒,未进行有效隔离,经过两轮传染后共有169人患新冠肺炎(假设每轮传染的人数相同).求:(1)、每轮传染中平均每个人传染了几个人?(2)、如果这些病毒携带者,未进行有效隔离,按照这样的传染速度,第三轮传染后,共有多少人患病?21. 如图,在▱ABCD中,AB=4,点D的坐标是(0,8),以点C为顶点的抛物线y=a(x﹣h)2+k经过x轴上的点A,B.
(1)、直接写出该二次函数的解析式为;(2)、不等式ax2+bx+c≤0的解集是;(3)、y随x的增大而减小的自变量x的取值范围是;(4)、若关于x的方程ax2+bx+c=k有两个不相等的实根,则k的取值范围是 .20. 2020年3月,新冠肺炎疫情在中国已经得到有效控制,但在全球却开始持续蔓延,这是对人类的考验,将对全球造成巨大影响.新冠肺炎具有人传人的特性,若一人携带病毒,未进行有效隔离,经过两轮传染后共有169人患新冠肺炎(假设每轮传染的人数相同).求:(1)、每轮传染中平均每个人传染了几个人?(2)、如果这些病毒携带者,未进行有效隔离,按照这样的传染速度,第三轮传染后,共有多少人患病?21. 如图,在▱ABCD中,AB=4,点D的坐标是(0,8),以点C为顶点的抛物线y=a(x﹣h)2+k经过x轴上的点A,B. (1)、求点A,B,C的坐标;(2)、若抛物线向上平移后恰好经过点D,求平移后抛物线的解析式.22. 如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象与x轴,y轴分别交于A、B、C三点,点D是其顶点,若C(0,2),D(2,4).
(1)、求点A,B,C的坐标;(2)、若抛物线向上平移后恰好经过点D,求平移后抛物线的解析式.22. 如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象与x轴,y轴分别交于A、B、C三点,点D是其顶点,若C(0,2),D(2,4). (1)、求抛物线解析式;(2)、在对称轴上找一点P,使AP+CP最小,求出点P的坐标.23. 某公司设计了一款工艺品,每件的成本是40元,为了合力定价,投放市场进行试销:据市场调查,销售单价是50元时,每天的销售量是100件,而销售单价每提高1元,每天就减少售出2件,但要求销售单价不得超过65元.(1)、若销售单价为每件60元,求每天的销售利润;(2)、要使每天销售这种工艺品盈利1350元,那么每件工艺品售价应为多少元?24. 列方程(组)解应用题:某驻村工作队,为带动群众增收致富,巩固脱贫攻坚成效,决定在该村山脚下,围一块面积为600m2的矩形试验茶园,便于成功后大面积推广.如图所示,茶园一面靠墙,墙长35m,另外三面用69m长的篱笆围成,其中一边开有一扇1m宽的门(不包括篱笆).求这个茶园的长和宽.
(1)、求抛物线解析式;(2)、在对称轴上找一点P,使AP+CP最小,求出点P的坐标.23. 某公司设计了一款工艺品,每件的成本是40元,为了合力定价,投放市场进行试销:据市场调查,销售单价是50元时,每天的销售量是100件,而销售单价每提高1元,每天就减少售出2件,但要求销售单价不得超过65元.(1)、若销售单价为每件60元,求每天的销售利润;(2)、要使每天销售这种工艺品盈利1350元,那么每件工艺品售价应为多少元?24. 列方程(组)解应用题:某驻村工作队,为带动群众增收致富,巩固脱贫攻坚成效,决定在该村山脚下,围一块面积为600m2的矩形试验茶园,便于成功后大面积推广.如图所示,茶园一面靠墙,墙长35m,另外三面用69m长的篱笆围成,其中一边开有一扇1m宽的门(不包括篱笆).求这个茶园的长和宽.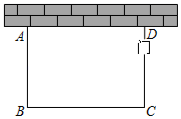 25. 如图,在△ABC中,∠C=90°,AC=12cm,BC=16cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动,当点Q到达点B时,点P也停止运动.
25. 如图,在△ABC中,∠C=90°,AC=12cm,BC=16cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动,当点Q到达点B时,点P也停止运动. (1)、如果P、Q同时出发,几秒钟后,可使△PCQ的面积为35平方厘米;(2)、点P、Q在移动过程中,是否存在某点时刻,使得△PCQ的面积等于△ABC的面积的四分之一?若存在,求出运动的时间;若不存在,说明理由.
(1)、如果P、Q同时出发,几秒钟后,可使△PCQ的面积为35平方厘米;(2)、点P、Q在移动过程中,是否存在某点时刻,使得△PCQ的面积等于△ABC的面积的四分之一?若存在,求出运动的时间;若不存在,说明理由.