广东省揭阳市五校22021-2022学年九年级上学期数学第一次月考试卷

试卷更新日期：2021-11-01 类型：月考试卷

进入出卷网下载

一、单选题

1. 由下表估算一元二次方程 $x^{2} + 12 x = 15$ 的一个根的范围，正确的是（）

$x$

1.0

1.0

1.2

1.3

$x^{2} + 12 x$

13

14.41

15.84

47.29

A、 $1.0 < x < 1.1$ B、 $1.1 < x < 1.2$ C、 $1.2 < x < 1.3$ D、 $14.41 < x < 15$

查看试题解析
2. 小明与小亮都是九（1）班的学生，在一次数学综合实践活动中，老师把全班同学随机分成四个小组，那么小明与小亮不在同一个小组的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、 $\frac{3}{4}$ D、 $\frac{5}{8}$

查看试题解析
3. 下列命题正确的是（）．

A、对角线相等的平行四边形是菱形 B、对角线相等且互相垂直的四边形是正方形 C、矩形的对角线互相垂直 D、顺次连接菱形各边中点，所得的四边形是矩形

查看试题解析
4. 已知一元二次方程 $x^{2} + k x + 3 = 0$ 有一个根为3，则 $k$ 的值为（）

A、2 B、-2 C、4 D、-4

查看试题解析
5. 如图，O是矩形ABCD的对角线AC的中点，M是CD边的中点．若AB＝12，OM＝4.5，则线段OB的长为（）．

A、6.5 B、7 C、7.5 D、8

查看试题解析
6. 已知关于x的方程mx²﹣2x+1＝0有两个不相等的实数根，则m的取值范围是（　　）

A、m＜1 B、m＞1 C、m＜1，且m≠0 D、m＞1，且m≠0

查看试题解析
7. 如图，在正方形ABCD中，AB＝3，点E，F分别在边AB，CD上，∠EFD＝60°．若将四边形EBCF沿EF折叠，点B恰好落在AD边上，则BE的长度为（）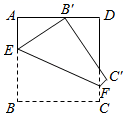

A、1 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、2

查看试题解析
8. 已知m、n是方程x²+x﹣2021＝0两根，则m²+2m+ $\frac{2021}{n}$ +1的值（　　）

A、0 B、2020 C、2022 D、无法确定

查看试题解析
9. 如图， $△$ ABC中，∠C＝90°，AC＝10，BC＝8，线段DE的两个端点D、E分别在边AC，BC上滑动，且DE＝6，若点M、N分别是DE、AB的中点，则MN的最小值为（）

A、10﹣ $\sqrt{41}$ B、 $\sqrt{41}$ ﹣3 C、2 $\sqrt{41}$ ﹣6 D、3

查看试题解析
10. 如图，在矩形ABCD中，AD＝ $\sqrt{2}$ AB，∠BAD的平分线交BC于点E．DH⊥AE于点H，连接BH并延长交CD于点F，连接DE交BF于点O，下列结论：①AD＝AE；②∠AED＝∠CED；③OE＝OD；④BH＝HF；⑤BC－CF＝2HE，其中正确的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

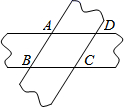
11. 在一个不透明的空袋子里，放入分别标有数字1，2，3，5的四个小球（除数字外其他完全相间），从中随机摸出2个小球，摸到的2个小球的数字之和恰为偶数的概率是．

查看试题解析
12. 在一个不透明的布袋里共装有80个红球和白球，这些球除颜色外完全相同，小明通过多次摸球试验后发现，摸到红色球的频率稳定在20%左右，则可以估计到布袋中红色球可能有个．

查看试题解析
13. 已知 $x = 2$ 是关于 $x$ 的方程 $x^{2} - (m + 4) x + 4 m = 0$ 的一个实数根，并且这个方程的两个实数根恰好是等腰 $△ A B C$ 的两条边长，则 $△ A B C$ 的周长为．

查看试题解析
14. 卫生部门为控制流感的传染，对某种流感研究发现：若一人患了流感，经过两轮传染后共有100人患了流感，若按此传染速度，第三轮传染中新患流感人数共有人.

查看试题解析
15. 如图，将两条宽度都为3的纸条重叠在一起，使 $∠ A B C = 60 °$ ，则四边形 $A B C D$ 的面积为．

查看试题解析
16. 如图，点O是正方形 $A B C D$ 的两条对角线的交点，过点O的直线与 $A D$ 、 $B C$ 交于点M、点N， $D E ⊥ M N$ ，交 $A B$ 于点E，若 $A M = \frac{1}{2}$ ， $D M = \frac{3}{2}$ ，则 $D E$ 的长为．

查看试题解析
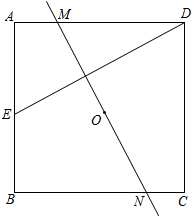17. 如图，将矩形ABCD放置在平面直角坐标系的第一象限内，使顶点A，B分别在x轴、y轴上滑动，矩形的形状保持不变，若AB=2，BC=1，则顶点C到坐标原点O的最大距离为.

查看试题解析

三、解答题

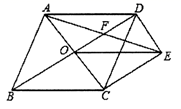
18. 小明在用配方法解方程x²﹣x﹣ $\frac{1}{2}$ ＝0时出现了不符合题意，解答过程如下：x²﹣x＝ $\frac{1}{2}$ （第一步）；x²﹣x+ $\frac{1}{4}$ ＝ $\frac{1}{2}$ + $\frac{1}{2}$ （第二步）；（x﹣ $\frac{1}{2}$ ）²＝1（第三步）；∴x₁＝﹣ $\frac{1}{2}$ ，x₂＝ $\frac{3}{2}$ （第四步）．

(1)、小明的解答过程是从第步开始出错的；

(2)、用配方法写出此题正确的解答过程．

查看试题解析
19. 如图，菱形 $A B C D$ 的对角线 $A C$ 、 $B D$ 相交于点 $O$ ，过点 $D$ 作 $D E / / A C$ 且 $D E = \frac{1}{2} A C$ ，连接 $C E$ 、 $O E$ ，连接 $A E$ 交 $O D$ 于点 $F$ .

(1)、求证： $O E = C D$ ；

(2)、若菱形 $A B C D$ 的边长为2， $∠ A B C = 60 °$ .求 $A E$ 的长.

查看试题解析
20. 吉林省已有六家国家5A级旅游景区，分别为a：长影世纪城；b：伪满皇宫博物院；c：长白山景区；d：六鼎山文化旅游区；e：长春世界雕塑园；f：天山天池．张帆同学与父母计划在十一期间从中选择部分景区游玩．

(1)、张帆一家选择e：长春世界雕塑园的概率是；

(2)、若张帆一家选择了e：长春世界雕塑园，他们再从a，b，c，d四个景区中任选两个景区去旅游，求选择a，d两个景区的概率（要求画树状图或列表求概率）．

查看试题解析
21. 2020年，受新冠肺炎疫情影响，口罩紧缺，某网店以每袋8元（一袋十个）的成本价购进了一批口罩，二月份以一袋14元的价格销售了256袋，三、四月该口罩十分畅销，销售量持续走高，在售价不变的基础上，四月份的销售量达到400袋．

(1)、二月的销售利润是元；

(2)、求三、四这两个月销售量的月平均增长率；

(3)、为回馈客户，该网店决定五月降价促销．经调查发现，在四月份销量的基础上，该口罩每袋降价1元，销售量就增加40袋，当口罩每袋降价多少元时，五月份可获利1920元？

查看试题解析
22. 为进一步推广大课间活动，某中学对已开设的A：实心球，B：立定跳远，C：跑步，D：跳绳这四种活动项目学生喜欢情况进行调查，随机抽取了部分学生调查，每位学生必选一项且只能选一项，将调查结果绘制成图1，图2的统计图，请结合图中的信息解答下列问题：

(1)、填空：被调查的学生共有 ▲ 名，并将两个统计图补充完整；

(2)、抽取了5名喜欢跑步的学生，其中有3名女生，2名男生，现从这5名学生中任意抽取2名学生，请用画树状图或列表的方法，求刚好抽到同性别学生的概率．

查看试题解析
23. 如图，点M，N分别在正方形ABCD的边BC，CD上，且∠MAN=45°，把△ADN绕点A顺时针旋转90°得到△ABE．

(1)、求证：∠EAM=45°；

(2)、求证：△AEM≌△ANM；

(3)、若BM=3，DN=2，求正方形ABCD的边长．

查看试题解析
24. 如图，在Rt△ABC中，∠C＝90°，AC＝20，∠A＝60°.点P从点B出发沿BA方向以每秒2个单位长度的速度向点A匀速运动，同时点Q从点A出发沿AC方向以每秒1个单位长度的速度向点C匀速运动，当其中一个点到达终点时，另一个点也随之停止运动.设点P、Q运动的时间是t秒.过点P作PM⊥BC于点M，连接PQ、QM.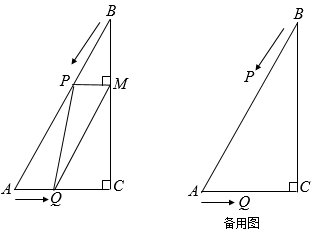

(1)、请用含有t的式子填空：AQ＝， AP＝， PM＝

(2)、是否存在某一时刻使四边形AQMP为菱形？如果存在，求出相应的t值；如果不存在，说明理由；

(3)、当t为何值时，△PQM为直角三角形？请说明理由.

查看试题解析
25. 如图

（问题情境）

如图1，四边形ABCD是正方形，M是BC边上的一点，E是CD边的中点，AE平分∠DAM．

（探究展示）

(1)、请你判断AM，AD，MC三条线段的数量关系，并说明理由；

(2)、AM = DE + BM是否成立？若成立，请给出证明；若不成立，请说明理由．

(3)、若四边形ABCD是长与宽不相等的矩形，其他条件不变，如图2，探究展示（1）、（2）中的结论是否仍然成立？请分别作出判断，不需要证明．

查看试题解析

$x$	1.0	1.0	1.2	1.3
$x^{2} + 12 x$	13	14.41	15.84	47.29