安徽省合肥市三校联考2021-2022学年九年级上学期数学第一次月考试卷
试卷更新日期:2021-11-01 类型:月考试卷
一、单选题
-
1. 下列函数属于二次函数的是( )A、 B、 C、 D、2. 二次函数y=3(x+4)2﹣5的图象的顶点坐标为( )A、(4,5) B、(﹣4,5) C、(4,﹣5) D、(﹣4,﹣5)3. 已知抛物线y=x2-x-1,与x轴的一个交点为(m,0),则代数式m2-m+2021的值为( )A、2019 B、2020 C、2021 D、20224. 如图,点 在二次函数 的图象上,则方程 解的一个近似值可能是( )
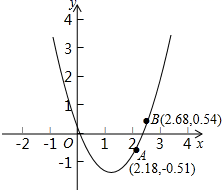 A、2.18 B、2.68 C、-0.51 D、2.455. 在同一坐标系中,作出函数y=kx2和y=kx﹣2(k≠0)的图象,只可能是( )A、
A、2.18 B、2.68 C、-0.51 D、2.455. 在同一坐标系中,作出函数y=kx2和y=kx﹣2(k≠0)的图象,只可能是( )A、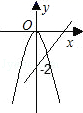 B、
B、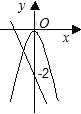 C、
C、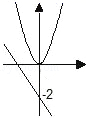 D、
D、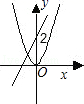 6. 点A(x1 , y1)、B(x2 , y2)、C(x3 , y3)都在反比例函数 的图象上,且x1<x2<0<x3 , 则y1、y2、y3的大小关系是( )A、y3<y1<y2 B、y1<y2<y3 C、y3<y2<y1 D、y2<y1<y37. k为任意实数,抛物线y=a(x﹣k)2﹣k(a≠0)的顶点总在( )A、直线y=x上 B、直线y=﹣x上 C、x轴上 D、y轴上8. 二次函数 ,当 时,则( )A、 B、 C、 D、9. 如图为抛物线y=ax2+bx+c的图象,A,B,C为抛物线与坐标轴的交点,且OA=OC=1,则下列关系中正确的是( )
6. 点A(x1 , y1)、B(x2 , y2)、C(x3 , y3)都在反比例函数 的图象上,且x1<x2<0<x3 , 则y1、y2、y3的大小关系是( )A、y3<y1<y2 B、y1<y2<y3 C、y3<y2<y1 D、y2<y1<y37. k为任意实数,抛物线y=a(x﹣k)2﹣k(a≠0)的顶点总在( )A、直线y=x上 B、直线y=﹣x上 C、x轴上 D、y轴上8. 二次函数 ,当 时,则( )A、 B、 C、 D、9. 如图为抛物线y=ax2+bx+c的图象,A,B,C为抛物线与坐标轴的交点,且OA=OC=1,则下列关系中正确的是( ) A、a+b=﹣1 B、a﹣b=﹣1 C、b<2a D、ac<010. 如图,点G、D、C在直线a上,点E、F、A、B在直线b上,若 , 从如图所示的位置出发,沿直线b向右匀速运动,直到EG与BC重合.运动过程中 与矩形ABCD重合部分的面积(S)随时间(t)变化的图象大致是( )
A、a+b=﹣1 B、a﹣b=﹣1 C、b<2a D、ac<010. 如图,点G、D、C在直线a上,点E、F、A、B在直线b上,若 , 从如图所示的位置出发,沿直线b向右匀速运动,直到EG与BC重合.运动过程中 与矩形ABCD重合部分的面积(S)随时间(t)变化的图象大致是( ) A、
A、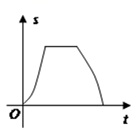 B、
B、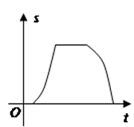 C、
C、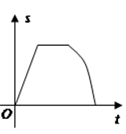 D、
D、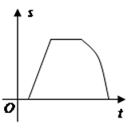
二、填空题
-
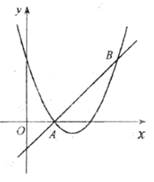
11. 若y=(m+2)x|m|+2x﹣1是二次函数,则m= .12. 把抛物线 向右平移2个单位,再向上平移4个单位,得到的抛物线的解析式是 .13. 如图,直线 和抛物线 都经过点 ,不等式 的解集.
 14. 如图,一抛物线型拱桥,当拱顶到水面的距离为2 m时,水面宽度为4 m;那么当水位下降1m后,水面的宽度为m.
14. 如图,一抛物线型拱桥,当拱顶到水面的距离为2 m时,水面宽度为4 m;那么当水位下降1m后,水面的宽度为m.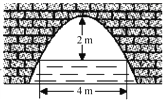
三、解答题
-
15. 已知函数y=(m2-2)x2+(m+ )x+8.(1)、若这个函数是一次函数,求m的值;(2)、若这个函数是二次函数,求m的取值范围.16. 已知抛物线的顶点为(1,-3),且经过点(2,-4),试确定该抛物线的函数表达式.17. 抛物线 .(1)、求顶点坐标,对称轴;(2)、x取何值时,y随x的增大而减小?(3)、x取何值时,y=0;x取何值时,y>0;x取何值时,y<0 .18. 已知:已知函数y = y1 +y2 , y1与x成正比例,y2与x成反比例,且当x = 1时,y =-1;当x = 3时,y = 5.求y关于x的函数关系式.19. 为应对全球爆发的新冠疫情,某疫苗生产企业于2021年1月份开始了技术改造,其月生分,技术改造完成后是一次函数图象的一部分,请根据图中数据解答下列问题:
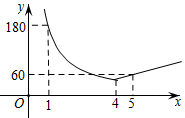 (1)、该疫苗生产企业4月份的生产数量为多少万支?(2)、该疫苗生产企业有多少个月的月生产数量不超过90万支?20. 在平面直角坐标系中,二次函数y= x2+bx+c的图象与x轴交于A(-2,0),B(4,0)两点,交y轴于点C,点P是第四象限内抛物线上的一个动点.
(1)、该疫苗生产企业4月份的生产数量为多少万支?(2)、该疫苗生产企业有多少个月的月生产数量不超过90万支?20. 在平面直角坐标系中,二次函数y= x2+bx+c的图象与x轴交于A(-2,0),B(4,0)两点,交y轴于点C,点P是第四象限内抛物线上的一个动点.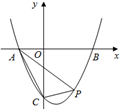 (1)、求二次函数的解析式;(2)、如图,连接AC,PA,PC,若S△PAC= ,求点P的坐标;21. 如图,已知A(-4,n),B(2,-4)是一次函数y1=kx+b的图像和反比例函数 的图像的两个交点
(1)、求二次函数的解析式;(2)、如图,连接AC,PA,PC,若S△PAC= ,求点P的坐标;21. 如图,已知A(-4,n),B(2,-4)是一次函数y1=kx+b的图像和反比例函数 的图像的两个交点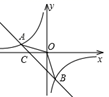 (1)、求反比例函数和一次函数的解析式(2)、求直线与x轴的交点C的坐标及△AOB的面积(3)、当x取何值时,y1=y2;当x取何值时,y1>y222. 为巩固“脱贫攻坚”成果,某驻村干部指导农户进行草莓种植和销售,已知草莓的种植成本为8元/千克,经市场调查发现,今年五一期间草莓的销售量 (千克)与销售单价 (元/千克) 成一次函数关系,下表列出了 与 的一些对应值:
(1)、求反比例函数和一次函数的解析式(2)、求直线与x轴的交点C的坐标及△AOB的面积(3)、当x取何值时,y1=y2;当x取何值时,y1>y222. 为巩固“脱贫攻坚”成果,某驻村干部指导农户进行草莓种植和销售,已知草莓的种植成本为8元/千克,经市场调查发现,今年五一期间草莓的销售量 (千克)与销售单价 (元/千克) 成一次函数关系,下表列出了 与 的一些对应值:16
24
32
168
144
120
(1)、根据表中信息,求 与 的函数关系式;(2)、若五一期间销售草莓获取的利润为 (元),请写出 与 之间函数表达式,并求出销售单价为多少时,获得的利润最大?最大利润是多少?(利润 销售额 成本)23. 如图,在平面直角坐标系 中,一次函数 的图象与反比例函数 的图象交于点 和点 .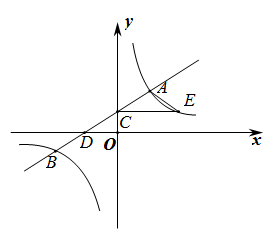 (1)、求一次函数与反比例函数的表达式;(2)、直线 与 轴交于点 ,与 轴交于点 .
(1)、求一次函数与反比例函数的表达式;(2)、直线 与 轴交于点 ,与 轴交于点 .①过点 作 轴交反比例函数 的图象于点 ,连接 ,试判断 的形状,并说明理由;
②设 是 轴上一点,当 时,求点 的坐标.