初中数学华师大版八年级上学期第14章勾股定理单元测试
试卷更新日期：2021-10-31 类型：单元试卷
一、单选题
-
1. 下列各组数中，是勾股数的是（ ）A、6，9，12 B、-9，40，41 C、9，12，13 D、7，24，252. 若一个直角三角形的两直角边的长分别为a，b，斜边长为c，则下列关于a，b，c的关系式中不正确的是（ ）A、b2=c2-a2 B、a2=c2-b2 C、b2=a2-c2 D、c2=a2+b23. 用反证法证明命题“在三角形中，至少有一个内角大于或等于60”时，首先假设这个三角形中（ ）A、三个内角都小于60° B、只有一个内角大于或等于60° C、至少有一个内角小于60° D、每一个内角都小于或等于60°4. 小明想知道学校旗杆的高，他发现旗杆上的绳子垂到地面还多 ，当他把绳子的下端拉开 后，发现下端刚好接触地面，则旗杆的高为（ ）A、 B、 C、 D、5. 我国古代数学著作《九章算术》中记载了一个问题：“今有池方一丈，葭（jiǎ）生其中，出水一尺，引葭赴岸，适与岸齐.间水深几何.”（丈、尺是长度单位，1丈 尺，）其大意为：有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺.如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面，水的深度是多少？则水深为（ ）
A、10尺 B、11尺 C、12尺 D、13尺6. 古埃及人曾经用如图所示的方法画直角：把一根长绳打上等距离的13个结，然后以3个结间距、4个结间距、5个结间距的长度为边长，用木桩钉成一个三角形，其中一角便是直角，这样做的道理是（ ）
A、直角三角形两个锐角互余 B、三角形内角和等于180° C、三角形任意两边之和大于第三边，任意两边之差小于第三边． D、如果三角形两边长的平方和等于第三边长的平方，那么这个三角形是直角三角形7. 如图所示，在△ABC中，∠A+∠B=∠C， BC= ， AB=4则AC的长是（ ）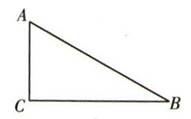
A、9 B、4 C、5 D、38. 如图是一个外轮廓为长方形的机器零件平面示意图，根据图中的尺寸(单位：mm)，计算两圆孔中心A和B的距离为（ ）mm．
A、90 B、100 C、120 D、1509. 如图所示，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙角的距离为0.7米，顶端距离地面2.4米．如果保持梯子底端位置不动，将梯子斜靠在右墙时，顶端距离地面2米，则小巷的宽度为（ ）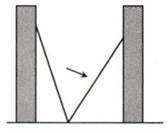
A、0.7米 B、1.5米 C、2.2米 D、2.4米10. 下列选项中，不能用来验证勾股定理的是（ ）A、
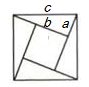B、
C、
D、
二、填空题
-
11. 在Rt△ABC中，∠C=90°，已知AB=25，AC=20，则BC=12. 如图是一参赛队员设计的机器人在比赛时行走的路径，机器人从 处先往东走 ，又往北走 ，遇到障碍后又往西走 ，再转向北走 往东拐，仅走 就到达了 .问 、 两点之间的距离为 .
13. 如图，已知圆柱的底面周长为10cm，高 为12cm， 是底面的直径，一只蚂蚁沿着圆柱侧面爬行觅食从点 爬到点 ，则蚂蚁爬行的最短路线为cm．
14. 如图，正方形 的边长分别为直角三角形的三边长，若正方形 的边长分别为 和2，则正方形 的面积为 ．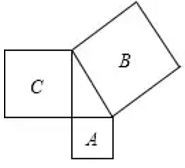
15. 如图所示，OC为∠AOB的平分线，CM⊥OB，OC=5，0M=4，则点C到射线OA的距离为
16. 如图，△ABC中，AB＝AC＝5，BC＝6，AD是BC边上的中线，F是AD上的动点，E是AC边上的动点，则CF+EF的最小值为.
三、解答题
-
17. 勾股定理被誉为“几何明珠”，在数学的发展历程中占有举足轻重的地位.它是初中数学中的重要知识点之一，也是初中学生以后解决数学问题和实际问题中常常运用到的重要知识，因此学好勾股定理非常重要.学习数学“不仅要知其然，更要知其所以然”，所以，我们要学会勾股定理的各种证明方法.请你利用如图图形证明勾股定理：
已知：如图，四边形ABCD中，BD⊥CD，AE⊥BD于点E，且△ABE≌△BCD.
求证：AB2＝BE2+AE2.
