初中数学华师大版八年级上学期第13章全等三角形单元测试
试卷更新日期:2021-10-31 类型:单元试卷
一、单选题
-
1. 用反证法证明命题:“已知△ABC,AB=AC,求证:∠B<90°.”第一步应先假设( )A、∠B≥90° B、∠B>90° C、∠B<90° D、AB≠AC2. 等腰三角形ABC中,AB=AC,AD是角平分线,则“①AD⊥BC,②BD=DC,③∠B=∠C,④∠BAD=∠CAD”中,结论正确的个数是( )A、4 B、3 C、2 D、13. 在△ABC中,AB=AC , ∠A=40°,则∠B的度数是( )A、70° B、55° C、50° D、40°4. 如图,△ABC≌△A'B'C',其中∠A=36°,∠C'=24°,则∠B=( )
 A、60° B、100° C、120° D、135°5. 如图,已知△ABC三条边、三个角,则甲、乙两个三角形中,与△ABC全等的图形是( )
A、60° B、100° C、120° D、135°5. 如图,已知△ABC三条边、三个角,则甲、乙两个三角形中,与△ABC全等的图形是( ) A、甲 B、乙 C、甲和乙 D、都不是6. 下列说法正确的是( )A、周长相等的两个三角形全等 B、如果三角形的三个内角满足∠A:∠B:∠C=1:2:3,则这个三角形是直角三角形 C、从直线外一点到这条直线的垂线段,叫做这点到直线的距离 D、两条直线被第三条直线所截,同位角相等7. 如图,已知 .添加一个条件后,可得 ,则在下列条件中,不能添加的是
A、甲 B、乙 C、甲和乙 D、都不是6. 下列说法正确的是( )A、周长相等的两个三角形全等 B、如果三角形的三个内角满足∠A:∠B:∠C=1:2:3,则这个三角形是直角三角形 C、从直线外一点到这条直线的垂线段,叫做这点到直线的距离 D、两条直线被第三条直线所截,同位角相等7. 如图,已知 .添加一个条件后,可得 ,则在下列条件中,不能添加的是 A、 B、 C、 D、8. 如图,在△ABC中,AC>BC,分别以点A,B为圆心,以大于 AB的长为半径画弧,两弧交于D,E,经过D,E作直线分别交AB,AC于点M,N,连接BN,下列结论正确的是( )
A、 B、 C、 D、8. 如图,在△ABC中,AC>BC,分别以点A,B为圆心,以大于 AB的长为半径画弧,两弧交于D,E,经过D,E作直线分别交AB,AC于点M,N,连接BN,下列结论正确的是( )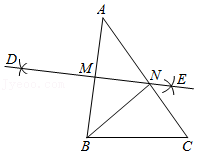 A、AN=NC B、AN=BN C、MN= BC D、BN平分∠ABC9. 如图,在 的正方形网格中有两个格点A、B,连接 ,在网格中再找一个格点C,使得 是等腰直角三角形,满足条件的格点C的个数是( )
A、AN=NC B、AN=BN C、MN= BC D、BN平分∠ABC9. 如图,在 的正方形网格中有两个格点A、B,连接 ,在网格中再找一个格点C,使得 是等腰直角三角形,满足条件的格点C的个数是( ) A、2 B、3 C、4 D、510. 如图,在△AOB和△COD中,OA=OB , OC=OD , OA<OC , ∠AOB=∠COD=36°.连接AC , BD交于点M , 连接OM . 下列结论:
A、2 B、3 C、4 D、510. 如图,在△AOB和△COD中,OA=OB , OC=OD , OA<OC , ∠AOB=∠COD=36°.连接AC , BD交于点M , 连接OM . 下列结论:①∠AMB=36°,②AC=BD , ③OM平分∠AOD , ④MO平分∠AMD . 其中正确的结论个数有( )个.
 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
11. 用反证法证明命题“在直角三角形中,至少有一个锐角不大于45°”第一步应假设.12. 已知一个等腰三角形的一个外角为82°,则这个等腰三角形的底角为.13. 如图,△ABC≌△DEC,∠ACD=28°,则∠BCE=°.
 14. 如图,在△ABC中,AB=AC , AB的中垂线DE交AC于点D , 交AB于点E , 如果BC=10,△DBC的周长为22,那么AB= .
14. 如图,在△ABC中,AB=AC , AB的中垂线DE交AC于点D , 交AB于点E , 如果BC=10,△DBC的周长为22,那么AB= . 15. 如图, 中, ,AD平分 , , ,则 的面积为 .
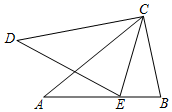
15. 如图, 中, ,AD平分 , , ,则 的面积为 . 16. 如图,在△ABC中,∠ACB=90°,点D是BC上的一点,AC=DC , AB⊥AE , 且AE=AB,连接DE交AC的延长线于点F , = ,则 = .
16. 如图,在△ABC中,∠ACB=90°,点D是BC上的一点,AC=DC , AB⊥AE , 且AE=AB,连接DE交AC的延长线于点F , = ,则 = .
三、作图题
-
17. 在如图的正方形网格中,每个小正方形的边长都是1,请在图中画出2个形状不同的等腰三角形,使它的腰长为 ,且顶点都在格点上,则满足条件的形状不同的等腰三角形共多少个.

四、解答题
-
18. 如图,在 中, .将 绕点 按逆时针方向旋转后得 ,连接 .当 时,求 的度数.
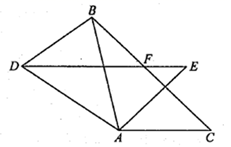 19. 如图, 是 的角平分线, , , .求证: .
19. 如图, 是 的角平分线, , , .求证: .
五、综合题
-
20. 在△ABC中,∠BAC=90°,AB=AC , 点E、点F分别是AB , AC上(不与B , C重合)的动点,点O是BC的中点,连接AO .
 (1)、如图1,当∠EOF=90°时,请问△AEO与△CFO全等吗?如果全等请证明,如果不是请说明理由;(2)、如图2,在(1)的条件下,过点O作OH⊥AC , 垂足为H,若AE=3,AF=9;请求HF的长。(3)、如图3,当∠EOF=45°时,连接EF , 若AO=5,AE:AF:EF=3:4:5,请求△AOF的面积.
(1)、如图1,当∠EOF=90°时,请问△AEO与△CFO全等吗?如果全等请证明,如果不是请说明理由;(2)、如图2,在(1)的条件下,过点O作OH⊥AC , 垂足为H,若AE=3,AF=9;请求HF的长。(3)、如图3,当∠EOF=45°时,连接EF , 若AO=5,AE:AF:EF=3:4:5,请求△AOF的面积.
-