初中数学华师大版八年级上学期第13章13.3.2等腰三角形的判定同步练习
试卷更新日期:2021-10-30 类型:同步测试
一、单选题
-
1. 下列三角形中,等腰三角形的个数是( )
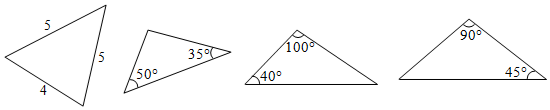 A、4个 B、3个 C、2个 D、1个2. 下列能断定△ABC为等腰三角形的是( )A、∠A=40°,∠B=50° B、∠A=2∠B=70° C、∠A=40°,∠B=70° D、AB=3,BC=6,周长为143. 如图, 中, , ,则 的度数为( )
A、4个 B、3个 C、2个 D、1个2. 下列能断定△ABC为等腰三角形的是( )A、∠A=40°,∠B=50° B、∠A=2∠B=70° C、∠A=40°,∠B=70° D、AB=3,BC=6,周长为143. 如图, 中, , ,则 的度数为( )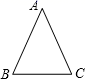 A、 B、 C、 D、4. 如图, , , ,则图中等腰三角形有( )
A、 B、 C、 D、4. 如图, , , ,则图中等腰三角形有( )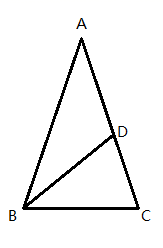 A、0个 B、1个 C、2个 D、3个5. 如图,△ABC为等边三角形,∠ABC、∠ACB的平分线相交于点O,OE∥AB交BC于点E,OF∥AC交BC于点F,则图中等腰三角形共有( )
A、0个 B、1个 C、2个 D、3个5. 如图,△ABC为等边三角形,∠ABC、∠ACB的平分线相交于点O,OE∥AB交BC于点E,OF∥AC交BC于点F,则图中等腰三角形共有( )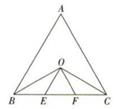 A、6个 B、5个 C、4个 D、3个6. 已知a、b、c是 的三条边,且满足 ,则 是( )A、锐角三角形 B、钝角三角形 C、等腰三角形 D、等边三角形7. 如图是5×5的正方形方格图,点A,B在小方格的顶点上,要在小方格的顶点确定一点C,连接AC和BC,使△ABC是等腰三角形,则方格图中满足条件的点C的个数是( )
A、6个 B、5个 C、4个 D、3个6. 已知a、b、c是 的三条边,且满足 ,则 是( )A、锐角三角形 B、钝角三角形 C、等腰三角形 D、等边三角形7. 如图是5×5的正方形方格图,点A,B在小方格的顶点上,要在小方格的顶点确定一点C,连接AC和BC,使△ABC是等腰三角形,则方格图中满足条件的点C的个数是( )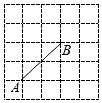 A、4 B、5 C、6 D、78. 如图, 为 内一点, 平分 , , ,若 , ,则 的长为( )
A、4 B、5 C、6 D、78. 如图, 为 内一点, 平分 , , ,若 , ,则 的长为( )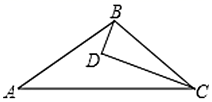 A、5 B、4 C、3 D、2
A、5 B、4 C、3 D、2二、填空题
-
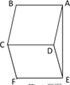
9. 在△ABC中,∠A=40°,∠C=70°,则△ABC是三角形.10. 如图,□ABCD和□DCFE的周长相等,∠B+∠F=220°,则∠DAE的度数为
 11. 如图,△ABC中AB=AC,D是AC上一点且BC=BD,若∠CBD=46°,则∠A=°.
11. 如图,△ABC中AB=AC,D是AC上一点且BC=BD,若∠CBD=46°,则∠A=°.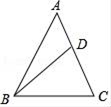 12. 如图,∠AOB=60°,OC平分∠AOB,P为射线OC上一点,如果射线OA上的点D满足△OPD是等腰三角形,那么∠ODP的度数为
12. 如图,∠AOB=60°,OC平分∠AOB,P为射线OC上一点,如果射线OA上的点D满足△OPD是等腰三角形,那么∠ODP的度数为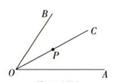 13. 如图,在 中, , , 是 的平分线,交 于点 , 是 的中点.连接 并延长,交 的延长线于点 ,连接 .写出图中三角形中所有的等腰三角形 .
13. 如图,在 中, , , 是 的平分线,交 于点 , 是 的中点.连接 并延长,交 的延长线于点 ,连接 .写出图中三角形中所有的等腰三角形 .
三、解答题
-
14. 如图所示,在△ABC中,∠ABC=2∠C,AD为BC边上的高,延长AB到E点,使BE=BD,连接ED并延长交AC于点F,请判断AF与FC的数量关系,并说明理由.
 15. 阅读材料:已知△ABC中,AD平分∠BAC,AD是△ABC的中线,求证:AB=AC.
15. 阅读材料:已知△ABC中,AD平分∠BAC,AD是△ABC的中线,求证:AB=AC.小明根据已知条件发现若AD平分∠BAC可得∠BAD=∠CAD,又AD是△ABC的中线,可得BD=CD,加上公共边的条件AD=AD,有两条边和一个角对应相等,就下结论得到△ABD和△ACD是全等的,从而得到结论∠B=∠C,可证出AB=AC成立;小芳的方法是用角平分线的性质得到DE=DF,再用中线分三角形的面积为相等两部分,再用等面积的方法可以得到结论.请你回答小明和小芳的证明思路谁正确的?请任选择一个方法进行完整的证明(可以与小明和小芳的方法不同)
