初中数学华师大版八年级上学期第13章13.2.6斜边直角边同步练习
试卷更新日期：2021-10-30 类型：同步测试
一、单选题
-
1. 如图，∠BAD＝∠BCD＝90°，AB＝CB，据此可以证明△BAD≌△BCD，证明的依据是 （ ）
A、AAS B、ASA C、SAS D、HL2. 用三角尺可按下面方法画角平分线：在已知∠AOB两边上分别取OM=ON ， 再分别过点M ， N作OA，OB的垂线，两垂线交于点P ， 画射线OP ， 则OP平分∠AOB ． 作图过程用到了△OPM≌△OPN ， 那么△OPM≌△OPN所用的判定定理是（ ）
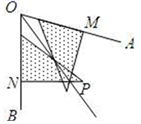A、SSS B、SAS C、HL D、ASA3. 如图，DE⊥AC于点E，BF⊥AC于点F，且DE=BF，若利用“HL”证明△DEC≌△BFA，则需添加的条件是（ ）
A、DC=BA B、EC=FA C、∠D=∠B D、∠DCE=BAF4. 下列判定直角三角形全等的方法，不正确的是（ ）A、两条直角边对应相等。 B、斜边和一锐角对应相等。 C、斜边和一条直角边对应相等。 D、两锐角相等。5. 如图，在△ABC中，∠ABC＝90°，AB＝CB ， F为AB延长线一点，点E在BC上，且AE＝CF ， ∠CAE＝30°，则∠ACF的度数是（ ）
A、75° B、60° C、55° D、45°6. 如图，锐角△ABC的两条高BD、CE相交于点O ， 且CE＝BD ， 若∠CBD＝20°，则∠A的度数为（ ）
A、20° B、40° C、60° D、70°7. 在 中， ，E是AB上一点，且 ，过E作 交AC于D，如果 ，则 等于（ ）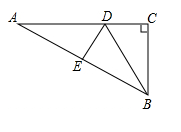
A、3cm B、4cm C、5cm D、6cm二、填空题
-
8. 如图， 中， 于D，要使 ，若根据“ ”判定，还需要加条件
9. 如图，∠A＝∠D＝90°，AC＝DB，则△ABC≌△DCB的理由是
10. 在 Rt△ABC 和 Rt△DEF 中，∠C=∠F=90°，AB=DE,AC=DF,所以 Rt△ABCRt△DEF.11. 如图，点A，E，F，C在一条直线上，若将△DEC的边EC沿AC方向平移，平移过程中始终满足下列条件：AE＝CF，DE⊥AC于点E，BF⊥AC于点F，且AB＝CD．则当点E，F不重合时，BD与EF的关系是 ．
12. 如图，点D在BC上，DE⊥AB于点E，DF⊥BC交AC于点F，BD＝CF，BE＝CD．若∠AFD＝145°，则∠EDF＝ ．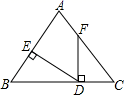
13. 如图，△ABC是边长为5的等边三角形，△BDC是顶角为120°的等腰三角形，以D为顶点作一个60°的∠MDN，点M、N分别在AB、AC上，连接MN，则△AMN的周长为 ．
三、作图题
-
14.
如图，在方格纸中，△PQR的三个顶点及A，B，C，D，E五个点都在小方格的顶点上，现以A，B，C，D，E中的三个点为顶点画三角形．
(1)在图甲中画出一个三角形与△PQR全等；
图甲
(2)在图乙中画出一个三角形与△PQR面积相等但不全等．
图乙四、解答题
-
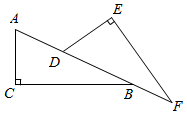
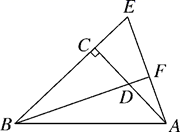
15. 如图，已知Rt△ABC中，∠ACB＝90°，CA＝CB，D是AC上一点，E在BC的延长线上，且AE＝BD，BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系，并说明你猜想的正确性.
-
