浙江省温州市四校2021-2022学年九年级上学期数学第一次联考试卷

试卷更新日期：2021-10-29 类型：月考试卷

进入出卷网下载

一、选择题（共10小题，每小题4分，共40分）.

1. 下列事件中，是必然事件的是（）

A、买一张电影票，座位号是3的倍数 B、一个盒子装有 $3$ 个红球和 $1$ 个白球，除颜色外其它完全相同，同时摸出两个球，一定会摸到红球 C、掷一枚质地均匀的硬币，正面向上 D、走过一个红绿灯路口时，前方正好是红灯

查看试题解析
2. 在一个不透明的袋子里装有2个红球和1个白球，它们除颜色外都相同，从中摸出一个球，放回搅匀后，再摸出一个球.两次都摸到红球的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{2}{9}$ D、 $\frac{4}{9}$

查看试题解析
3. 一个不透明的袋子里装有黄、白、红三种颜色的球，摇匀后每次随机从袋中摸出一个球，记录颜色后放回袋中，通过多次试验后，发现摸到红球的频率稳定在0.5，则摸到红球的概率约为（）

A、0.25 B、0.5 C、0.75 D、0.85

查看试题解析
4. 设A(−2，y₁)，B(1，y₂)，C(2，y₃)是抛物线y=−x²-2x+2上的三点，则y₁ ， y₂ ， y₃的大小关系为（）

A、 $y_{1}$ > $y_{2}$ > $y_{3}$ B、 $y_{1}$ > $y_{3}$ > $y_{2}$ C、 $y_{3}$ > $y_{2}$ > $y_{1}$ D、 $y_{3}$ > $y_{1}$ > $y_{2}$

查看试题解析
5. 二次函数 $y = - 3 {(x + 1)}^{2} - 7$ 得顶点坐标是（）

A、 $(1 ， 7)$ B、 $(1 ， - 7)$ C、 $(- 1 ， 7)$ D、 $(- 1 ， - 7)$

查看试题解析
6. 抛物线y＝﹣2x²经过平移后得到y＝﹣2（x+3）²﹣4，其平移方法是（）

A、向右平移3个单位，再向下平移4个单位 B、向右平移3个单位，再向上平移4个单位 C、向左平移3个单位，再向下平移4个单位 D、向左平移3个单位，再向上平移4个单位

查看试题解析
7. 如图，有一抛物线形拱桥，当拱顶离水面 $2 m$ 时，水面宽 $4 m$ ，当水面宽增加 $(2 \sqrt{6} - 4) m$ 时，则水面应下降的高度是（）

A、 $2 m$ B、 $1 m$ C、 $\sqrt{6} m$ D、 $(\sqrt{6} - 2) m$

查看试题解析
8. 笼子里关着一只小松鼠（如图），笼子的主人决定把小松鼠放归大自然，将笼子所有的门都打开，松鼠要先经过第一道门（A，B，或C），再经过第二道门（D或E）才能出去.问松鼠走出笼子的路线（经过的两道门）有（）种不同的可能？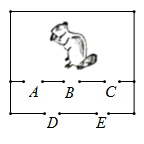

A、12 B、6 C、5 D、2

查看试题解析
9. 如图，在平面直角坐标系中，抛物线y= $\frac{1}{3}$ x²经过平移得到抛物线y=ax²+bx，其对称轴与两段抛物线所围成的阴影部分的面积为 $\frac{2}{3}$ ，则a、b的值分别为（）

A、 $\frac{1}{3}$ ， $\frac{4}{3}$ B、 $\frac{1}{3}$ ，﹣ $\frac{2}{3}$ C、 $\frac{1}{3}$ ，﹣ $\frac{4}{3}$ D、﹣ $\frac{1}{3}$ ， $\frac{4}{3}$

查看试题解析
10. 如图，若二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 图象的对称轴为 $x = 1$ ，与y轴交于点C，与x轴交于点A，点 $B (- 1 ， 0)$ ，则①二次函数的最大值为 $a + b + c$ ；② $a - b + c < 0$ ；③ $b^{2} - 4 a c < 0$ ；④当 $y > 0$ 时， $- 1 < x < 3$ .其中正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（本题有6小题，每小题5分，共30分）

11. 半径是2的圆，如果半径增加x时，增加的面积s与x之间的关系表达式为.

查看试题解析
12. 已知二次函数y＝（x+m）²+2，当x＞2时，y的值随x值的增大而增大，则实数m的取值范围是.

查看试题解析
13. 在一个不透明的袋子里装有4个黄球和2个红球，这些球除颜色外完全相同. 从袋中任意摸出1个球是红球，则这个事件是事件（填“随机”或“必然”或“不可能”）

查看试题解析
14. 如图所示的两个圆盘中，指针落在每一个数上的机会均等，则两个指针同时落在偶数上的概率是.

查看试题解析
15. 有三张背面完全相同，正面分别写有如下二次函数：① $y = x^{2} + 3$ ；② $y = x^{2} - 2 x + 1$ ；③ $y = 2 x^{2} - x - 3$ ，从中随机抽取1张，则抽出的二次函数的图象与 $x$ 轴没有交点的概率是.

查看试题解析
16. 如图，线段AB=10，点P在线段AB上，在AB的同侧分别以AP、BP为边长作正方形APCD和BPEF，点M、N分别是EF、CD的中点，则MN的最小值是.

查看试题解析

三、解答题（本题有8小题，共80分.解答需写出必要的文字说明、演算步骤或证明过程）

17. 一个批发商从某服装制造公司购进了50包型号为L的衬衫，由于包装工人疏忽，在包裹中混进了型号为M的衬衫.每包中混入的M号衬衫数见下页表：

M号衬衫数	0	1	4	5	7	9	10	11
包数	7	3	10	15	5	4	3	3

一位零售商从50包中任意选取了一包，求下列事件的概率：

(1)、包中没有混入M号衬衫；

(2)、包中混入M号衬衫数不超过7；

(3)、包中混入M号衬衫数超过10.

查看试题解析

18. 甲口袋中装有2个相同的小球，它们分别写有字母A和B；乙口袋中装有3个相同的小球，它们分别写有字母C，D和E；丙口袋中装有2个相同的小球，它们分别写有字母H和I.从三个口袋中各随机取出1个小球.
（本题中，A，E，I是元音字母；B，C，D，H是辅音字母.）

(1)、取出的3个小球上恰好有1个、2个和3个元音字母的概率分别是多少？

(2)、取出的3个小球上全是辅音字母的概率是多少？

查看试题解析
19. 已知抛物线的解析式为y＝﹣3x²+6x+9．

(1)、求此抛物线的对称轴；

(2)、直接写出抛物线与x坐标轴的交点坐标．

查看试题解析
20. 小明同学在用描点法画二次函数 $y = a {(x - 1)}^{2} + k$ 图象时，由于粗心，他算错了一个y值，列出了下面表格：

x

…

﹣1

0

1

2

3

…

y＝ax²+bx+c

…

5

3

2

3

6

…

(1)、请指出这个错误的y值，并说明理由；

(2)、若点M（m，y₁），N（m+4，y₂）在二次函数y＝ax²+bx+c图象上，且m＞1，试比较y₁与y₂的大小.

查看试题解析
21. 如图，已知抛物线y＝﹣x²+bx+c经过A（﹣1，0），B（3，0）两点.

(1)、求抛物线的解析式和顶点坐标；

(2)、当0＜x＜3时，直接写出y的取值范围；

(3)、点P为抛物线上一点，若S_△PAB＝10，求出此时点P的坐标.

查看试题解析
22. 某中学在艺术节期间向全校学生征集书画作品，美术王老师从全校随机抽取了四个班级记作A、B、C、D，对征集到的作品的数量进行了分析统计，制作了如下两幅不完整的统计图．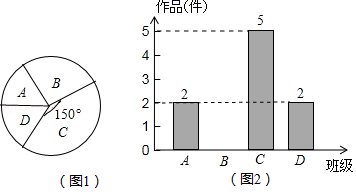

(1)、王老师抽查的四个班级共征集到作品多少件？

(2)、请把图2的条形统计图补充完整；

(3)、若全校参展作品中有四名同学获得一等奖，其中有二名男生、二名女生．现在要在其中抽两名同学去参加学校总结表彰座谈会，请用画树状图或列表的方法求恰好抽中一名男生一名女生的概率．

查看试题解析
23. 某商店经销一种销售成本为30元/kg的水产品，据市场分析：若按50元/kg销售，一个月能售出300kg，销售单价每涨1元，月销售量就减少10kg.针对这种水产品，请解答以下问题：

(1)、设售价为x元/kg，月销售量ykg，请问售价涨了元，月销售量y（kg）与售价x（元/kg）之间的函数解析式为.

(2)、当售价定为多少时，月销售利润最大？最大利润是多少？

(3)、商店想在月销售成本不超过6000元的情况下，使得月销售利润不少于4000元，销售单价可定在什么范围？

查看试题解析
24. 如图，抛物线y＝ax²+bx（a＞0）过点E（8，0），矩形ABCD的边AB在线段OE上（点A在点B的左侧），点C、D在抛物线上，∠BAD的平分线AM交BC于点M，点N是CD的中点，已知OA＝2，且OA：AD＝1：3.

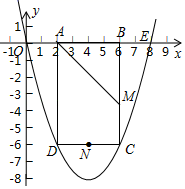(1)、求抛物线的解析式；

(2)、F、G分别为x轴，y轴上的动点，顺次连接M、N、G、F构成四边形MNGF，求四边形MNGF周长的最小值；

(3)、在x轴下方且在抛物线上是否存在点P，使△ODP中OD边上的高为 $\frac{6 \sqrt{10}}{5}$ ？若存在，求出点P的坐标；若不存在，请说明理由；

查看试题解析

x	…	﹣1	0	1	2	3	…
y＝ax²+bx+c	…	5	3	2	3	6	…