浙江省杭州市余杭区三校2021-2022学年八年级上学期数学第一次联考试卷
试卷更新日期:2021-10-29 类型:月考试卷
一、选择题(每小题3分,共30分)
-
1. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知△ABC的三条边分别为a,b,c,化简|a+b﹣c|﹣|b﹣a﹣c|+|a﹣b+c|( )A、3a﹣b+c B、a+b﹣c C、a﹣b﹣c D、﹣a+3b﹣3c3. 对于命题“如果 ,那么 ”,能说明它是假命题的反例是( )A、 , B、 , C、 D、4. 如图,∠1,∠2,∠3,∠4的关系为( )
2. 已知△ABC的三条边分别为a,b,c,化简|a+b﹣c|﹣|b﹣a﹣c|+|a﹣b+c|( )A、3a﹣b+c B、a+b﹣c C、a﹣b﹣c D、﹣a+3b﹣3c3. 对于命题“如果 ,那么 ”,能说明它是假命题的反例是( )A、 , B、 , C、 D、4. 如图,∠1,∠2,∠3,∠4的关系为( )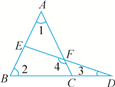 A、∠1+∠2=∠4-∠3 B、∠1+∠2=∠3+∠4 C、∠1-∠2=∠4-∠3 D、∠1-∠2=∠3-∠45. 如图,在 中, , ,观察图中尺规作图的痕迹,则 的度数为( )
A、∠1+∠2=∠4-∠3 B、∠1+∠2=∠3+∠4 C、∠1-∠2=∠4-∠3 D、∠1-∠2=∠3-∠45. 如图,在 中, , ,观察图中尺规作图的痕迹,则 的度数为( )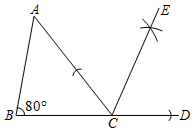 A、65° B、70° C、75° D、80°6. 如图, 是等边三角形,两个锐角都是 的三角尺的一条直角边在 上,则 的度数为( )
A、65° B、70° C、75° D、80°6. 如图, 是等边三角形,两个锐角都是 的三角尺的一条直角边在 上,则 的度数为( )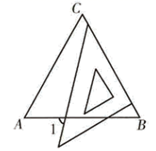 A、 B、 C、 D、7. 下列命题的逆命题正确的是( )A、两条直线平行,内错角相等 B、若两个实数相等,则它们的绝对值相等 C、全等三角形的对应角相等 D、若两个实数相等,则它们的平方也相等8. 如图, 中, ,将 沿DE翻折,使点A与点B重合,则CE的长为( )
A、 B、 C、 D、7. 下列命题的逆命题正确的是( )A、两条直线平行,内错角相等 B、若两个实数相等,则它们的绝对值相等 C、全等三角形的对应角相等 D、若两个实数相等,则它们的平方也相等8. 如图, 中, ,将 沿DE翻折,使点A与点B重合,则CE的长为( )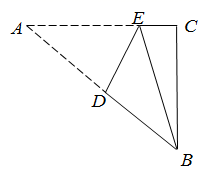 A、 B、2 C、 D、9. 如图,点 是 的中点, , , 平分 ,下列结论:① ;② ;③ ;④ .其中正确的是( )
A、 B、2 C、 D、9. 如图,点 是 的中点, , , 平分 ,下列结论:① ;② ;③ ;④ .其中正确的是( ) A、①②④ B、①②③④ C、②③④ D、①③10. 一次数学课上,老师请同学们在一张长为18厘米,宽为16厘米的矩形纸板上,剪下一个腰长为10厘米的等腰三角形,且要求等腰三角形的一个顶点与矩形的一个顶点重合,其它两个顶点在矩形的边上,则剪下的等腰三角形的面积为多少平方厘米( )A、50 B、50或40或20 C、50或30或20 D、50或40或30
A、①②④ B、①②③④ C、②③④ D、①③10. 一次数学课上,老师请同学们在一张长为18厘米,宽为16厘米的矩形纸板上,剪下一个腰长为10厘米的等腰三角形,且要求等腰三角形的一个顶点与矩形的一个顶点重合,其它两个顶点在矩形的边上,则剪下的等腰三角形的面积为多少平方厘米( )A、50 B、50或40或20 C、50或30或20 D、50或40或30二、填空题(每小题4分,共24分)
-
11. 如图, ,∠A=45°,∠ACD=80°,则∠DBC的度数为°.
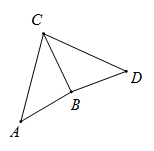 12. 如图, , , 分别是 三边延长线上的点, ,则 °.
12. 如图, , , 分别是 三边延长线上的点, ,则 °.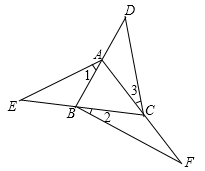 13. 如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.则∠DAC=°.
13. 如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.则∠DAC=°.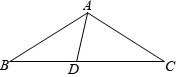 14. 如图, ABC中,∠A=90,∠ABC=60°,以顶点B为圆心,适当长为半径画弧,分别交边AB,BC于点E,F;再分别以E,F为圆心,以大于 EF长为半径作弧,两弧在∠ABC内交于点P,作射线BP,交边AC于点G,若 ABG的面积为5cm2 , 则 BCG的面积为cm2.
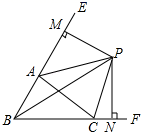
14. 如图, ABC中,∠A=90,∠ABC=60°,以顶点B为圆心,适当长为半径画弧,分别交边AB,BC于点E,F;再分别以E,F为圆心,以大于 EF长为半径作弧,两弧在∠ABC内交于点P,作射线BP,交边AC于点G,若 ABG的面积为5cm2 , 则 BCG的面积为cm2.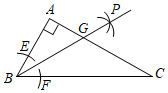 15. 如图, ABC中,∠ABC、∠EAC的角平分线BP、AP交于点P,延长BA、BC,PM⊥BE,PN⊥BF,则下列结论中正确的是.
15. 如图, ABC中,∠ABC、∠EAC的角平分线BP、AP交于点P,延长BA、BC,PM⊥BE,PN⊥BF,则下列结论中正确的是.①CP平分∠ACF;②∠ABC+2∠APC=180°;③∠ACB=2∠APB;④S△PAC=S△MAP+S△NCP.
 16. 如图,在直角三角形 中,直角边 , ,以它的三边分别作出了正方形 、 、 ,把 、 、 的面积分别记为 、 、 ,则 .
16. 如图,在直角三角形 中,直角边 , ,以它的三边分别作出了正方形 、 、 ,把 、 、 的面积分别记为 、 、 ,则 .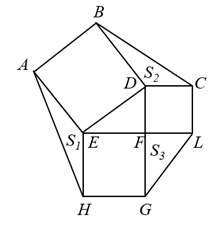
三、解答题(共66分)
-
17. 如图,AB∥CD,∠ABE=∠DCF.求证:∠E=∠F.

18. 如图△ADF≌△BCE,∠B=40°,∠F=22°,BC=2cm,CD=1cm.求: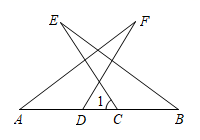 (1)、∠1的度数;
(1)、∠1的度数;
(2)、AC的长.
19. 两个大小不同的等腰直角三角形三角板,如图①所示放置,图②是由它抽象的几何图形,B、C、E在同一条直线上,连接DC. (1)、找出图②的中的全等三角形,并给予证明.(2)、求证DC⊥BE.20. 如图,在 中, , ,点D是 上一动点,连接 ,过点A作 ,并且始终保持 ,连接 .
(1)、找出图②的中的全等三角形,并给予证明.(2)、求证DC⊥BE.20. 如图,在 中, , ,点D是 上一动点,连接 ,过点A作 ,并且始终保持 ,连接 . (1)、求证: ;(2)、若 平分 交 于F,若 , ,求 的长.21. 如图所示,点M是线段AB上一点,ED是过点M的一条直线,连接AE、BD,过点B作BF AE交ED于F,且EM=FM.
(1)、求证: ;(2)、若 平分 交 于F,若 , ,求 的长.21. 如图所示,点M是线段AB上一点,ED是过点M的一条直线,连接AE、BD,过点B作BF AE交ED于F,且EM=FM.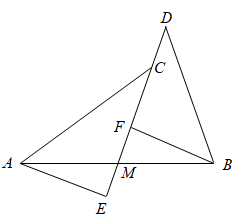 (1)、若AE=5,求BF的长;(2)、若∠AEC=90°,∠DBF=∠CAE,求证:CD=FE.22. 如图,在△ABC中,AB=AC,∠B=50°,点D在线段BC上运动(不与点B,C重合),连接AD,作∠ADE=50°,DE交线段AC于点E.
(1)、若AE=5,求BF的长;(2)、若∠AEC=90°,∠DBF=∠CAE,求证:CD=FE.22. 如图,在△ABC中,AB=AC,∠B=50°,点D在线段BC上运动(不与点B,C重合),连接AD,作∠ADE=50°,DE交线段AC于点E.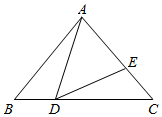 (1)、当∠BDA=100°时,∠BAD=°,∠DEC=°;(2)、当DC=AB时,△ABD和△DCE是否全等?请说明理由;(3)、在点D的运动过程中,是否存在△ADE是等腰三角形的情形?若存在,请直接写出此时∠BDA的度数,若不存在,请说明理由.23. 在 中, .
(1)、当∠BDA=100°时,∠BAD=°,∠DEC=°;(2)、当DC=AB时,△ABD和△DCE是否全等?请说明理由;(3)、在点D的运动过程中,是否存在△ADE是等腰三角形的情形?若存在,请直接写出此时∠BDA的度数,若不存在,请说明理由.23. 在 中, .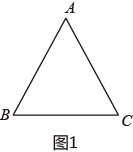
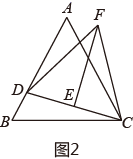
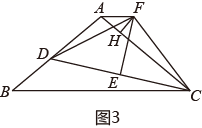 (1)、如图1、求证: :(2)、如图2,D为AB上一点,连接CD,E为CD中点,过点E作 于点E,连接 ,求证: ;(3)、如图3,在(2)的条件下,过点F作 于点H,连接AF,若 AF∥BC,FH=4,CH=20,BD=10 ,求 的面积
(1)、如图1、求证: :(2)、如图2,D为AB上一点,连接CD,E为CD中点,过点E作 于点E,连接 ,求证: ;(3)、如图3,在(2)的条件下,过点F作 于点H,连接AF,若 AF∥BC,FH=4,CH=20,BD=10 ,求 的面积