苏科版初中数学八年级上册 2.3 设计轴对称图形 同步训练
试卷更新日期：2021-10-29 类型：同步测试
一、单选题
-
1. 在下列某品牌T恤的四个洗涤说明图案的设计中，没有运用轴对称知识的是（ ）A、
B、
C、
D、
2. 我国主要银行的商标设计基本上都融入了中国古代钱币的图案，如图是我国四个银行的商标图案，其中是轴对称图形的有（ ）
A、①②③ B、①②④ C、①③④ D、②③④3. 如图，正方形网格中，已有两个小正方形被涂黑，再涂黑另外一个小正方形，使整个被涂黑的图案构成一个轴对称图形的方法有（ ）
A、5 B、6 C、4 D、74. 把一张正方形纸片按如图所示的方法对折两次后剪去两个角，那么打开以后的形状是（ ）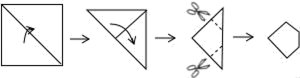
A、六边形 B、八边形 C、十二边形 D、十六边形5. 小军同学在网格纸上将某些图形进行平移操作，他发现平移前后的两个图形所组成的图形可以是轴对称图形.如图所示，现在他将正方形 从当前位置开始进行一次平移操作，平移后的正方形的顶点也在格点上，则使平移前后的两个正方形组成轴对称图形的平移方向有（ ）
A、3个 B、4个 C、5个 D、无数个二、填空题
-
6. 在图案设计中常用的作图工具有 ， ， ．7. 如图，图①经过变换得到图②；图①经过变换得到图③；图①经过变换得到图④．（填“平移”、“旋转”或“轴对称”）
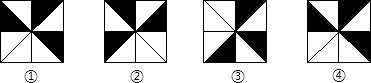8. 如图，正三角形网格中，已有两个小正三角形被涂黑，再将图中其余小正三角形涂黑一个，使整个被涂黑的图案构成一个轴对称图形的方法有种．
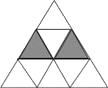9. 如图4×5的方格纸中，在除阴影之外的方格中任意选择一个涂黑，与图中阴影部分构成轴对称图形的涂法有 种．
10. 在如图的方格纸上画有2条线段，若再画1条线段，使图中的三条线段组成一个轴对称图形，则这条线段的画法最多有种．
11. 在4×4的方格中有五个同样大小的正方形如图摆放，移动其中一个正方形到空白方格中，与其余四个正方形组成的新图形是一个轴对称图形，这样的移法共有种．
12. 如图，有一个以格点为顶点的△ABC，请你找出格纸中所有与△ABC成轴对称且也以格点为顶点的三角形，这样的三角形共有个，它们分别是 ．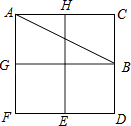
三、作图题
-
13. 如图1为 形的一种三格骨牌，它是由三个全等的正方形连接而成.请以 形的三格骨牌为基本图形，在图2，图3中各设计一个轴对称图形，要求如下：
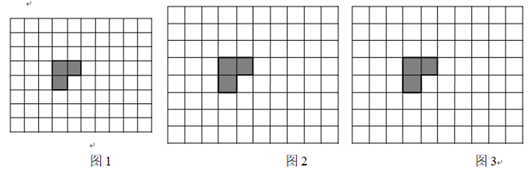(1)、每个图形由两个 形三格骨牌组成，骨牌的顶点都在小正方形的顶点上.(2)、设计的图形用斜线涂出，若形状相同，则视为一种.14. 把图中的各图补画成以l为对称轴的轴对称图形．
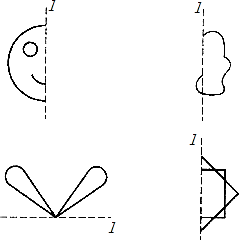15. 如图，有六个正六边形，在每个正六边形里有六个顶点，要求用两个顶点连线（即正六边形的对角线）将正六方形分成若干块，相邻的两块用黑白两色分开．最后形成轴对称图形，图中已画出三个，请你继续画出三个不同的轴对称图形（至少用两条对角线）
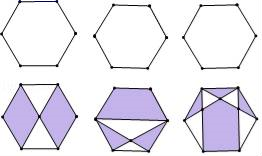16. 如图是由16个小正方形组成的正方形网格图，现已将其中的两个涂黑，请你用三种不同的方法分别在下图中再涂黑三个空白的小正方形，使它成为轴对称图形．
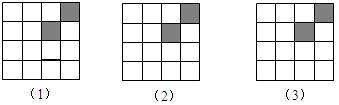17. 利用网格作图，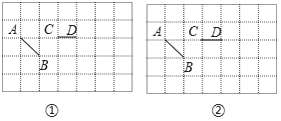
①请你在图①中画出线段AB关于线段CD所在直线成轴对称的图形；
②请你在图②中添加一条线段，使图中的3条线段组成一个轴对称图形．请画出所有情形．
四、解答题
-
18. 利用1个等腰三角形、2个长方形、3个圆，可以构造出许多独特且有意义的轴对称图形，如图已给出四幅图，你能再构思出一些轴对称图形吗(画出3个即可)?别忘了加一两句贴切、有创意的解说词.
19. 如图，是由4×4个大小完在一样的小正方形组成的方格纸，其中有两个小正方形是涂黑的，请再选择三个小正方形并涂黑，使图中涂黑的部分成为轴对称图形.并画出它的一条对称轴(如图例.画对一个得1分)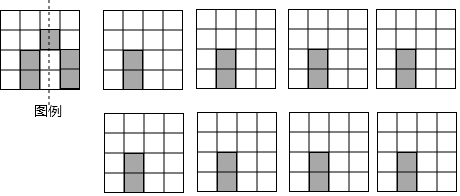
20. 解答题。(1)、如图，在“4×4”正方形网格中，已有2个小正方形被涂黑．请你分别在下面2张图中再若干个空白的小正方形涂黑，使得涂黑的图形成为轴对称图形．（图（1）要求只有1条对称轴，图（2）要求只有2条对称轴）．
(2)、在3×3的正方形格点图中，有格点△ABC和△DEF，且△ABC和△DEF关于某直线成轴对称，请在备用图中画出4个这样的△DEF．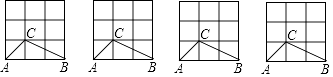
21. 如图，方格纸中每个小方格都是边长为1的正方形，我们把以格点连线为边的多边形称为“格点多边形”．如图（一）中四边形ABCD就是一个“格点四边形”．
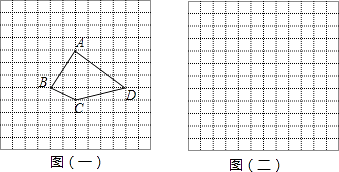(1)、作出四边形ABCD关于直线BD对称的四边形A′B′C′D′；(2)、求图（一）中四边形ABCD的面积；(3)、在图（二）方格纸中画一个格点三角形EFG，使△EFG的面积等于四边形ABCD的面积且△EFG为轴对称图形．22.按要求作图
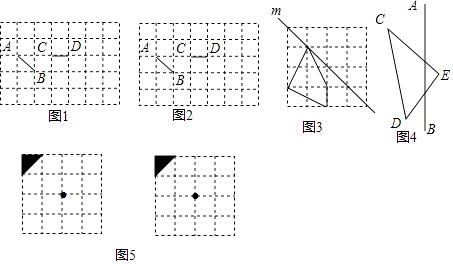(1)、利用网格作图，①请你在图1中画出线段CD关于线段AB所在直线成轴对称的图形；
②请你在图2中添加一条线段，使图中的3条线段组成一个轴对称图形．请画出所有情形；
③如图3作出四边形关于直线m对称的图形．
④如图4所示以AB为对称轴，画出已知图形的轴对称图形．
(2)、如图5是一个4×4的正方形网格，每个小正方形的边长为1．请你在网格中以左上角的三角形为基本图形，通过平移、对称变换，设计一个精美图案，使其满足；（设计两幅）①轴对称图形；
②所作图案用阴影标识，且阴影部分的面积为4．