苏科版初中数学八年级上册 1.3 探索三角形全等的条件-SSS 同步训练 (基础版)
试卷更新日期:2021-10-29 类型:同步测试
一、单选题
-
1. 用直尺和圆规作一个角等于已知角的示意图如图,则说明 ,两个三角形全等的依据是( )
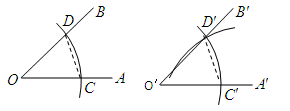 A、 B、 C、 D、不能确定2. 如图,在 与 中, , .若 ,则 的度数为( )
A、 B、 C、 D、不能确定2. 如图,在 与 中, , .若 ,则 的度数为( )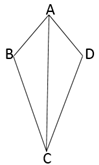 A、52 ° B、62° C、72° D、118°3. 如图, 中, , ,直接使用“SSS”可判定( )
A、52 ° B、62° C、72° D、118°3. 如图, 中, , ,直接使用“SSS”可判定( )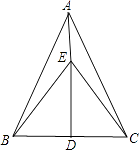 A、 ≌ B、 ≌ C、 ≌ D、 ≌4.
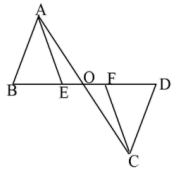
A、 ≌ B、 ≌ C、 ≌ D、 ≌4.如图,AB=CD,AC=BD,且AC交BD于点O,在原图形的基础上,用SSS证明△AOB≌△COD,还需添加的一个条件是( )
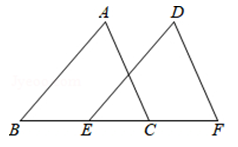
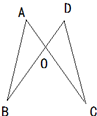 A、OB=OC B、∠A=∠D C、∠B=∠C D、AB∥CD5. 如图,点A,D,C,F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,依据“SSS”还需要添加一个条件是( )
A、OB=OC B、∠A=∠D C、∠B=∠C D、AB∥CD5. 如图,点A,D,C,F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,依据“SSS”还需要添加一个条件是( )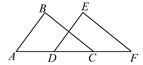 A、AD=CD B、AD=CF C、BC∥EF D、DC=CF6. 如图,若 ,则 的度数是( )
A、AD=CD B、AD=CF C、BC∥EF D、DC=CF6. 如图,若 ,则 的度数是( )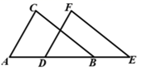 A、 B、 C、 D、7. 如图,在 和 中,已知 ,还需添加两个条件才能使 ,添加的一组条件不正确的是
A、 B、 C、 D、7. 如图,在 和 中,已知 ,还需添加两个条件才能使 ,添加的一组条件不正确的是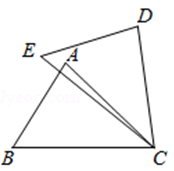 A、 , B、 , C、 , D、 ,8. 如图, , ,则下列结论中,不正确的是( )
A、 , B、 , C、 , D、 ,8. 如图, , ,则下列结论中,不正确的是( )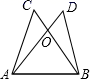 A、 B、 C、 D、9. 如图,已知: , , , ,则 ( )
A、 B、 C、 D、9. 如图,已知: , , , ,则 ( )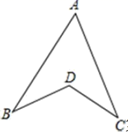 A、 B、 C、 或 D、10. 已知△ABC的三边长分别为3,4,5,△DEF的三边长分别为3,3x﹣2,2x+1,若这两个三角形全等,则x的值为( )A、2 B、2或 C、 或 D、2或 或
A、 B、 C、 或 D、10. 已知△ABC的三边长分别为3,4,5,△DEF的三边长分别为3,3x﹣2,2x+1,若这两个三角形全等,则x的值为( )A、2 B、2或 C、 或 D、2或 或二、填空题
-
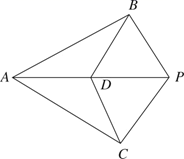
11. 如图是小明制作的风筝,他根据DE=DF, EH=FH,不用度量就通过证全等三角形知道∠DEH=∠DFH,试问小明判定这两个全等三角形的方法是(用字母表示).
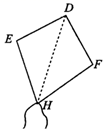 12. 如图,已知:在ΔABC中,AC=DB , 如果要用“SSS”证明∆ABC≌∆DCB , 则应该增加的条件是.
12. 如图,已知:在ΔABC中,AC=DB , 如果要用“SSS”证明∆ABC≌∆DCB , 则应该增加的条件是.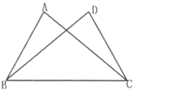 13. 如图,已知AB=AD,那么添加条件后,就能判定△ABC≌△ADC.
13. 如图,已知AB=AD,那么添加条件后,就能判定△ABC≌△ADC. 14. 如图,已知AC=AD , 要证明△ABC≌△ABD , 还需添加的条件是 . (只写出一个条件即可),并根据你所填的条件证明△ABC≌△ABD .
14. 如图,已知AC=AD , 要证明△ABC≌△ABD , 还需添加的条件是 . (只写出一个条件即可),并根据你所填的条件证明△ABC≌△ABD .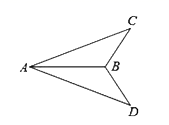 15. 如图,已知AD=BC,根据“SSS”,还需要一个条件 , 可证明△ABC≌△BAD;根据“SAS”,还需要一个条件 , 可证明△ABC≌△BAD.
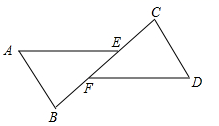
15. 如图,已知AD=BC,根据“SSS”,还需要一个条件 , 可证明△ABC≌△BAD;根据“SAS”,还需要一个条件 , 可证明△ABC≌△BAD.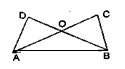 16. 如图,在 和 中, , ,当添加条件时,就可得到 .(只需填写一个你认为正确的条件)
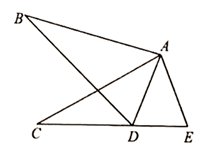
16. 如图,在 和 中, , ,当添加条件时,就可得到 .(只需填写一个你认为正确的条件)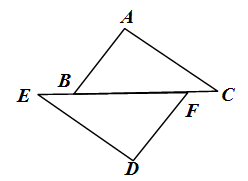 17. 已知:如图,点 在同一直线上, , ,则 .
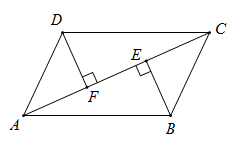
17. 已知:如图,点 在同一直线上, , ,则 .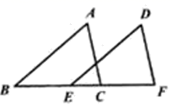 18. 如图,在四边形ABCD中, , ,E是AC上的点,则图中共有对全等三角形.
18. 如图,在四边形ABCD中, , ,E是AC上的点,则图中共有对全等三角形.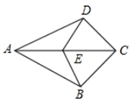
三、解答题
-
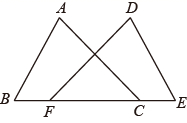
19. 如图,点B、F、C、E在同一条直线上,点A、D在直线BC的异侧,AB=DE,AC=DF,BF=EC.求证:△ABC≌△DEF.
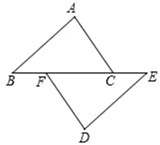 20. 如图,点C , F在BE上,BF=EC , AB=DE , AC=DF .
20. 如图,点C , F在BE上,BF=EC , AB=DE , AC=DF .求证:∠A=∠D .