苏科版初中数学八年级上册 1.3 探索三角形全等的条件-ASA 同步训练 (基础版)
试卷更新日期:2021-10-29 类型:同步测试
一、单选题
-
1. 如图,乐乐书上的三角形墨迹污染了一部分,很快他就画出一个三角形与书上的三角形全等,这两个三角形全等的依据是( )
 A、 B、 C、 D、2. 如图,在△ABD与△ACD中,已知∠CAD=∠BAD,在不添加任何辅助线的前提下,依据“ASA”证明△ABD≌△ACD,需再添加一个条件,正确的是( )A、∠B=∠C B、∠BDE=∠CDE C、AB=AC D、BD=CD3. 花花不慎将一块三角形的玻璃打碎成了如图所示的四块(图中所标①、②、③、④),若要配一块与原来大小一样的三角形玻璃,应该带( )
A、 B、 C、 D、2. 如图,在△ABD与△ACD中,已知∠CAD=∠BAD,在不添加任何辅助线的前提下,依据“ASA”证明△ABD≌△ACD,需再添加一个条件,正确的是( )A、∠B=∠C B、∠BDE=∠CDE C、AB=AC D、BD=CD3. 花花不慎将一块三角形的玻璃打碎成了如图所示的四块(图中所标①、②、③、④),若要配一块与原来大小一样的三角形玻璃,应该带( )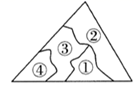 A、第①块 B、第②块 C、第③块 D、第④块4. 如图,AC=DF,∠1=∠2,如果根据“ASA”判定△ABC≌△DEF,那么需要补充的条件是( )
A、第①块 B、第②块 C、第③块 D、第④块4. 如图,AC=DF,∠1=∠2,如果根据“ASA”判定△ABC≌△DEF,那么需要补充的条件是( )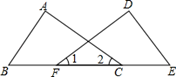 A、∠A=∠D B、AB=DE C、∠A=∠E D、∠B=∠E5. 如图, ,若依据“ASA”证明 ,则需添加的一个条件是( )
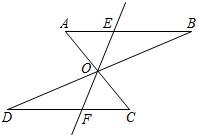
A、∠A=∠D B、AB=DE C、∠A=∠E D、∠B=∠E5. 如图, ,若依据“ASA”证明 ,则需添加的一个条件是( ) A、 B、 C、 D、6. 如图,AD、BC相交于点O, , ,下列结论中,错误的是( )
A、 B、 C、 D、6. 如图,AD、BC相交于点O, , ,下列结论中,错误的是( ) A、 B、 C、 D、7. 如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ,已知PQ=5,NQ=9,则MH的长为( )
A、 B、 C、 D、7. 如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ,已知PQ=5,NQ=9,则MH的长为( ) A、3 B、4 C、5 D、68. 如图,点B、C、E在同一条直线上,∠B=∠E=∠ACF=60°,AB=CE,则下列与BC相等的线段是( )
A、3 B、4 C、5 D、68. 如图,点B、C、E在同一条直线上,∠B=∠E=∠ACF=60°,AB=CE,则下列与BC相等的线段是( ) A、AC B、AF C、CF D、EF9. 如图, 的面积为 , 为 的角平分线,过点A作 于P,则 的面积为( )
A、AC B、AF C、CF D、EF9. 如图, 的面积为 , 为 的角平分线,过点A作 于P,则 的面积为( ) A、 B、 C、 D、10. 如图,已知▱OABC的顶点A,C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为( )
A、 B、 C、 D、10. 如图,已知▱OABC的顶点A,C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为( ) A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
11. 已知,如图:∠ABC=∠DEF,AB=DE,要说明△ABC≌△DEF,若以“ASA”为依据,还要添加的条件为.
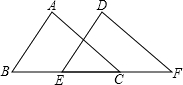 12. 如图,点B,F,C,E在同一直线上,BF=CE,AB∥DE,要说明△ABC≌△DEF,若以“ASA”为依据,还要添加的条件为.
12. 如图,点B,F,C,E在同一直线上,BF=CE,AB∥DE,要说明△ABC≌△DEF,若以“ASA”为依据,还要添加的条件为. 13. 如图,已知AB=AC,D、E分别为AB、AC上两点,∠B=∠C,AC=8cm,AD=5cm,则CE=cm.
13. 如图,已知AB=AC,D、E分别为AB、AC上两点,∠B=∠C,AC=8cm,AD=5cm,则CE=cm. 14. 如图,已知AB∥CF,E为DF的中点.若AB=13cm,CF=7cm,则BD=cm.
14. 如图,已知AB∥CF,E为DF的中点.若AB=13cm,CF=7cm,则BD=cm.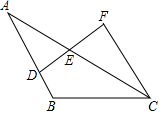 15. 如图,点 在 上, ,则 .
15. 如图,点 在 上, ,则 . 16. 在Rt ,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5cm,则AE=cm.
16. 在Rt ,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5cm,则AE=cm.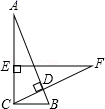 17. 如图,在等腰直角△ABC中,∠A=90°,AB=AC,D为边BC中点,DE⊥DF,若四边形AEDF的面积是4,则等腰直角△ABC的面积为 .
17. 如图,在等腰直角△ABC中,∠A=90°,AB=AC,D为边BC中点,DE⊥DF,若四边形AEDF的面积是4,则等腰直角△ABC的面积为 . 18. △ABC和△A′B′C′中,已知∠A=∠B′,AB=B′C′,增加条件可使△ABC≌△B′C′A′(ASA).
18. △ABC和△A′B′C′中,已知∠A=∠B′,AB=B′C′,增加条件可使△ABC≌△B′C′A′(ASA).三、解答题
-
19. 如图,已知点B,C,F,E在同一直线上,∠1=∠2,BC=EF,AB∥DE.求证:AC=DF.
 20. 如图,已知点 , , , 在同一条直线上, ,且 , .求证: .
20. 如图,已知点 , , , 在同一条直线上, ,且 , .求证: . 21. 如图, 于 于 .
21. 如图, 于 于 .求证: .
 22. 如图,点D在 上,点E在 上, , ,求证: .
22. 如图,点D在 上,点E在 上, , ,求证: .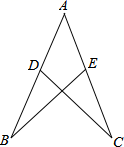 23. 已知,如图,∠1=∠2,∠C=∠D,BC=BD,求证: ABD≌ EBC.
23. 已知,如图,∠1=∠2,∠C=∠D,BC=BD,求证: ABD≌ EBC.