辽宁省大连市瓦房店市2021-2022学年七年级上学期数学第一次月考试卷
试卷更新日期:2021-10-28 类型:月考试卷
一、单选题
-
1. 的相反数是( )A、 B、 C、3 D、-32. 在﹣ ,1,0,﹣ 这四个数中,最小数是( )A、﹣ B、1 C、0 D、﹣3. 下列等式中不成立的是( )A、|﹣3|=3 B、﹣|﹣3|=﹣|﹣3| C、﹣|﹣3|=3 D、|﹣3|=|3|4. 如图所示的图形为四位同学画的数轴,其中正确的是( )A、
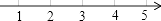 B、
B、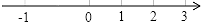 C、
C、 D、
D、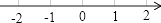 5. 如果 ,下列成立的是( )A、 B、 C、 D、6. -a一定是( )A、正数 B、负数 C、正数或负数 D、正数或零或负数7. 一个数和它的倒数相等,则这个数是( )A、1 B、 C、±1 D、±1和08. 下列说法:
5. 如果 ,下列成立的是( )A、 B、 C、 D、6. -a一定是( )A、正数 B、负数 C、正数或负数 D、正数或零或负数7. 一个数和它的倒数相等,则这个数是( )A、1 B、 C、±1 D、±1和08. 下列说法:①一个数的绝对值一定不是负数;
②一个数的相反数一定是负数;
③两个数的和一定大于每一个加数;
④若ab>0,则a与b都是正数;
⑤一个非零数的绝对值等于它的相反数,那么这个数一定是负数,
其中正确说法的个数是( )个.
A、1 B、2 C、3 D、49. 数轴上一动点A向左移动3个单位长度到达点B,再向右移动5个单位长度到达点C.若点C表示的数为1,则点A表示的数为( )A、﹣1 B、﹣2 C、﹣3 D、310. 点A,B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:① ;② ;③ ;④ .其中正确的是( ) A、①③ B、③④ C、①② D、②④
A、①③ B、③④ C、①② D、②④二、填空题
-
11. 计算:﹣9+2= .12. -5的倒数是;-5的绝对值是 .13. 在体育课的跳远比赛中,以2.00米为标准,若小东跳出了1.85米,记作﹣0.15米,那么小东跳了2.23米,可记作 米.14. 比较大小:+(﹣ ) ﹣|﹣ |.15. 用科学记数法可以将12800000表示为 .16. 已知|a|=6,|b|=4,且ab<0,则a+b的值为 .
三、解答题
-
17. 把下列各数填在相应的大括号里.
8, ,0.275,0, ,π,﹣0.25,﹣|﹣2|.
分数:{ ⋯};
非负整数:{ ⋯};
有理数:{ ⋯}.
18. 把﹣(﹣1),4,﹣22 , |﹣1 |,0分别表示在数轴上,并用“<”号把它们连接起来.19. 若|a-1|+|b+3|=0,则 的值为多少?20. 计算题(1)、﹣7+13﹣6+20;(2)、1+(﹣2)+|﹣2﹣3|﹣5;(3)、(﹣5)×(﹣7)×2×(﹣6);(4)、﹣14﹣(1﹣ )×22+(﹣3)2 .21. 已知a、b互为相反数,c、d互为倒数,m的绝对值是2,求 的值.22. 对于有理数a、b,定义一种新运算“⊕”,规定:a⊕b=|a+b|﹣|a﹣b|.(1)、计算2⊕(﹣3)的值;(2)、若a⊕a=8,求a的值.23. 已知a,b为有理数,且他们在数轴上的位置如图所示.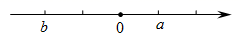 (1)、试判断a,b的正负性;(2)、在数轴上标出a,b相反数的位置;(3)、根据数轴化简:|a|=;|b|=;|﹣a|=;
(1)、试判断a,b的正负性;(2)、在数轴上标出a,b相反数的位置;(3)、根据数轴化简:|a|=;|b|=;|﹣a|=;|﹣b|= .
(4)、若|a|=2,|b|=3.5,求a﹣b的值.24. 一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:单位(米)+5,﹣3,+10,﹣8,﹣3,+12,﹣10.(1)、守门员最后是否回到了球门线的位置.(2)、在练习过程中,守门员离开球门线最远距离是多少米?(3)、守门员全部练习结束后,他共跑了多少米?25. 定义:我们把数轴上两点所对应的数的差的绝对值叫做数轴上两点间的距离,例:点A、B在数轴上分别对应的数为a、b,则A、B两点间的距离表示为AB=|a﹣b|.
根据以上知识解题:
(1)、数轴上A、B两点表示的数分别为a、b,当a=2,b=﹣3时,①AB的距离是;
②若数轴上一点M,MA+MB最小值为;
(2)、数轴上两点A、B表示的数为x、﹣2,①A、B之间的距离可用含x的式子表示为: ,
②若该两点之间的距离为3,那么x值为 ;
(3)、若点A表示的数为4,点B表示的数为﹣2,点P从点A出发,以每秒3个单位长度的速度沿射线AB匀速运动,设运动时间为t秒(t>0).①t秒后,PB=;(用含t的式子表示)
②若点P到点A的距离等于点P到点B的距离的2倍,求t值.