山东省济宁市邹城市2021-2022学年八年级上学期数学第一次月考试卷
试卷更新日期:2021-10-28 类型:月考试卷
一、单选题
-
1. 为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条,这样做的道理是( )
 A、两点之间,线段最短 B、垂线段最短 C、三角形具有稳定性 D、两直线平行,内错角相等2. 如图,为估计南开中学桃李湖岸边 两点之间的距离,小华在湖的一侧选取一点 ,测到 米, 米,则 间的距离可能是( )
A、两点之间,线段最短 B、垂线段最短 C、三角形具有稳定性 D、两直线平行,内错角相等2. 如图,为估计南开中学桃李湖岸边 两点之间的距离,小华在湖的一侧选取一点 ,测到 米, 米,则 间的距离可能是( ) A、5米 B、15米 C、25米 D、30米3. 如图所示,如果将一副三角板按如图方式叠放,那么 ∠1 等于( )
A、5米 B、15米 C、25米 D、30米3. 如图所示,如果将一副三角板按如图方式叠放,那么 ∠1 等于( ) A、 B、 C、 D、4. 如图,∠BDC=98°,∠C=38°,∠A=37°,则∠B的度数是( )
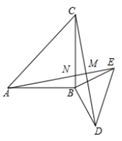
A、 B、 C、 D、4. 如图,∠BDC=98°,∠C=38°,∠A=37°,则∠B的度数是( ) A、33° B、23° C、27° D、37°5. 如图,在△ABC中,∠A=50°,∠1=30°,∠2=40°,∠D的度数是( )
A、33° B、23° C、27° D、37°5. 如图,在△ABC中,∠A=50°,∠1=30°,∠2=40°,∠D的度数是( )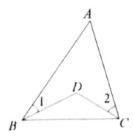 A、110° B、120° C、130° D、140°6. 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( )
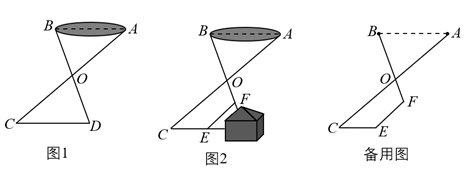
A、110° B、120° C、130° D、140°6. 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( )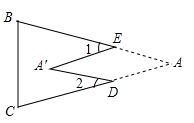 A、∠A=∠1+∠2 B、2∠A=∠1+∠2 C、3∠A=2∠1+∠2 D、3∠A=2(∠1+∠2)7. 小明一笔画成了如图所示的图形,则 的度数为( )
A、∠A=∠1+∠2 B、2∠A=∠1+∠2 C、3∠A=2∠1+∠2 D、3∠A=2(∠1+∠2)7. 小明一笔画成了如图所示的图形,则 的度数为( ) A、360° B、540° C、600° D、720°8. 如果,在 中, , , 是 边上的高, 是 的平分线,则 的度数为( )
A、360° B、540° C、600° D、720°8. 如果,在 中, , , 是 边上的高, 是 的平分线,则 的度数为( )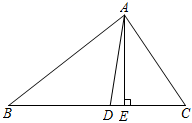 A、8° B、10° C、12° D、14°9. 如图,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE交于O,连结AO,则图中共有全等三角形的对数为( )
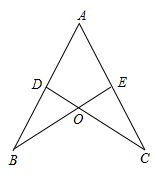
A、8° B、10° C、12° D、14°9. 如图,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE交于O,连结AO,则图中共有全等三角形的对数为( ) A、2对 B、3对 C、4对 D、5对10. 如图,给出下列四组条件:
A、2对 B、3对 C、4对 D、5对10. 如图,给出下列四组条件:①AB=DE,BC=EF,AC=DF;
②AB=DE,∠B=∠E.BC=EF;
③∠B=∠E,BC=EF,∠C=∠F;
④AB=DE,AC=DF,∠B=∠E.
其中,能使△ABC≌△DEF的条件共有( )
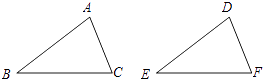 A、1组 B、2组 C、3组 D、4组
A、1组 B、2组 C、3组 D、4组二、填空题
-
11. 如图,在四边形ABCD中,AB∥CD , 连接BD . 请添加一个适当的条件 , 使 .(只需写一个)
 12. 如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=°.
12. 如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=°.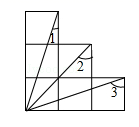 13. 如图,已知BD为△ABC中∠ABC的平分线,CD为△ABC中的外角∠ACE的平分线,与BD交于点D , 若∠D=∠α , 试用∠α表示∠A , ∠A= .
13. 如图,已知BD为△ABC中∠ABC的平分线,CD为△ABC中的外角∠ACE的平分线,与BD交于点D , 若∠D=∠α , 试用∠α表示∠A , ∠A= . 14. 如图,已知 的顶点分别为 , , ,存在点D使 与 全等,则点D的坐标是 .
14. 如图,已知 的顶点分别为 , , ,存在点D使 与 全等,则点D的坐标是 . 15. 如图,AB=12cm , CA⊥AB于A , DB⊥AB于B , 且AC=4cm , P点从B向A运动,速度为1cm/s , Q点从B向D运动,速度为2cm/s , P、Q两点同时出发,运动秒后△CAP与△PQB全等.
15. 如图,AB=12cm , CA⊥AB于A , DB⊥AB于B , 且AC=4cm , P点从B向A运动,速度为1cm/s , Q点从B向D运动,速度为2cm/s , P、Q两点同时出发,运动秒后△CAP与△PQB全等.
三、解答题
-
16. 如图, 中, , , 平分 , 于D, 交 于F,求 的度数.
 17. 如图,在 与 中, , , .
17. 如图,在 与 中, , , . (1)、求证: ;(2)、若 , ,求 的度数.18. 如图,点B、E、C、F在同一条直线上, , , .求证: .
(1)、求证: ;(2)、若 , ,求 的度数.18. 如图,点B、E、C、F在同一条直线上, , , .求证: . 19. 如图,在 与 中, , ,点D在 边上, .试判断 与 的数量关系,并说明理由.
19. 如图,在 与 中, , ,点D在 边上, .试判断 与 的数量关系,并说明理由.