广东省湛江市霞山区2021-2022学年八年级上学期数学10月月考试卷
试卷更新日期：2021-10-28 类型：月考试卷
一、单选题
-
1. 如果一个多边形的内角和等于720°，则它的边数为（ ）A、3 B、4 C、5 D、62. 下列图形中，正确画出AC边上的高的是（ ）A、
B、
C、
D、
3. 一个三角形的两边长分别为2和5，且第三边长为整数，这样的三角形的周长最大值是( )A、 B、 C、 D、4. 如图，已知△ABC中，∠C=90°，若沿图中虚线剪去∠C，则∠1+∠2等于（ ）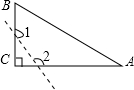
A、90° B、135° C、270° D、315°5. 如图，AD是 的中线，已知 的周长为25cm，AB比AC长6cm，则 的周长为（ ）
A、19cm B、22cm C、25cm D、31cm6. 在下列条件：① ；② ；③ ；④ 中，能确定 ABC是直角三角形的条件有（ ）A、1个 B、2个 C、3个 D、4个7. 如图， ， ，垂足分别为D、E，且 ，则直接判定 与 全等的理由是（ ）
A、SAS B、AAS C、SSS D、HL8.△ABC中，BF、CF是角平分线，∠A=70°，则∠BFC=（ ）
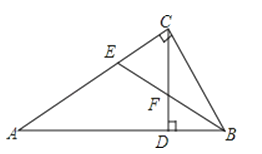
A、125° B、110° C、100° D、150°9.如图，已知△ABC中，∠ACB=90°，CD为AB边上的高，∠ABC的平分线BE分别交CD、CA于点F、E，则下列结论正确的有（ ）
①∠CFE=∠CEF；②∠FCB=∠FBC，③∠A=∠DCB；④∠CFE与∠CBF互余．
A、①③④ B、②③④ C、①②④ D、①②③10. 如图，Rt△ACB中，∠ACB＝90°，△ABC的角平分线AD、BE相交于点P，过P作PF⊥AD交BC的延长线于点F，交AC于点H，则下列结论：①∠APB＝135°；②BF＝BA；③PH＝PD；④连接CP，CP平分∠ACB，其中正确的是（ ）
A、①②③ B、①②④ C、①③④ D、①②③④二、填空题
-
11. 一个多边形的内角和为1080°，则它的边数为 ． 它的外角和为°．12. 如图，AB＝DC ， BF＝EC ， 点B、F 、E、C在同一条直线上，补充一个条件，能使△ABE≌△DCF的是 ． （填序号）①AE＝DF；②AE// DF；③AB// DC；④2∠A＝∠D ．
13. 如图，AB＝AD ， CB＝CD ， ∠B＝30°，∠BAD＝48°，则∠ACD的度数是 ．
14. 如图， 中， 于D，要使 ，若根据“ ”判定，还需要加条件
15. 如图所示，在△ABC中，∠B=∠C=50°，BD=CF，BE=CD，则∠EDF的度数是.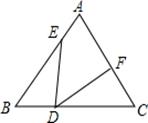
16. 如图所示，△ABO与△CDO称为“对顶三角形”，其中∠A+∠B=∠C+∠D．利用这个结论，在图2中，∠A+∠B+∠C+∠D+∠E+∠F+∠G=
17. 如图，OB平分∠MON ， A为 OB的中点，AE⊥ON于点 E ， AE＝4，D为 OM上一点，BC OM交 DA于点 C ， 则CD的最小值为 ．
三、解答题
-
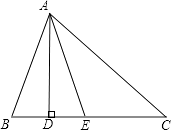
18. 如图，在△ABC中，∠B＞∠C，AD⊥BC，垂足为D，AE平分∠BAC．已知∠B=65°，∠DAE=20°，求∠C的度数．
19. 已知：如图， ，求线段 的长．
20. 已知：△ABC中，∠B=∠A+10°，∠C=∠A+20°，求三角形的各个内角度数.21. 如图，点D、B分别在∠A的两边上，C是∠A内一点，且AB=AD，BC=DC，CE⊥AD，CF⊥AB，垂足分别为E、F．求证：CE=CF．
22. 如图，点E在CD上，BC与AE交于点F，AB＝CB，BE＝BD，∠1＝∠2．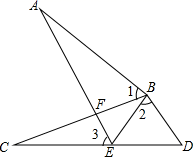
(1)、求证：AE＝CD；(2)、证明：∠1＝∠3．23. 如图，在△ABC中，AD平分∠BAC ， ∠C＝90°，DE⊥AB于点E ， 点F在AC上，BD＝DF ．
(1)、求证：CF＝EB；(2)、若AB＝14，AF＝8，求CF的长．24. 如图所示，点M是线段AB上一点，ED是过点M的一条直线，连接AE、BD，过点B作BF AE交ED于F，且EM=FM．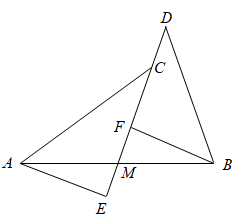
(1)、若AE=5，求BF的长；(2)、若∠AEC=90°，∠DBF=∠CAE，求证：CD=FE．25. 已知点C为线段AB上一点，分别以AC ， BC为边在线段AB同侧作△ACD 和△BCE ， 且CA＝CD ， CB＝CE ， ∠ACD＝∠BCE ， 直线AE与BD交于点F ．
(1)、如图1，若∠ACD＝58°，求∠BCE的度数．(2)、如图2，将图1中△ACD绕点C顺时针旋转任意角度（交点F至少在BD ， AE中的一条线段上）①请直接写出∠EFB与∠ECB的数量关系；
②若∠ACD＝α ，试探究∠AFB 与α的数量关系，并予以证明．
(3)、如图3，若∠ACD＝α，连AB ， 求∠BAE一∠ABD的值．