广东省揭阳市五校2021-2022学年八年级上学期数学第一次月考试卷
试卷更新日期:2021-10-28 类型:月考试卷
一、单选题
-
1. 下列一组数:﹣8,2.7, , ,0.66666…,0,2,0.080080008…(相邻两个8之间依次增加一个0)其中是无理数的有( )A、0个 B、1个 C、2个 D、3个2. 已知 ,则 的值为( )A、0 B、1 C、 D、20203. 的平方根是( )A、2 B、-2 C、 D、4. 下列各组数中,能构成直角三角形的一组是( )A、1,2,3 B、1,1, C、2,3,4 D、7,15,175. 如图,矩形ABCD的边AD在数轴上,若点A与数轴上表示数1的点重合,AB=1,以点A为圆心,对角线AC的长为半径作弧与数轴负半轴交于一点,则该点表示的数为( )
 A、﹣3 B、 C、 +1 D、 ﹣16. 下列计算正确的是( )A、 B、 C、 D、7. 我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为 ,则该三角形的面积为 ,现已知∆ 的三边长分别为 ,则∆ 的面积为( )A、 B、 C、 D、8. 如图,有一个圆柱,底面圆的直径AB= ,高BC=12cm,P为BC的中点,一只蚂蚁从A点出发沿着圆柱的表面爬到P点的最短距离为
A、﹣3 B、 C、 +1 D、 ﹣16. 下列计算正确的是( )A、 B、 C、 D、7. 我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为 ,则该三角形的面积为 ,现已知∆ 的三边长分别为 ,则∆ 的面积为( )A、 B、 C、 D、8. 如图,有一个圆柱,底面圆的直径AB= ,高BC=12cm,P为BC的中点,一只蚂蚁从A点出发沿着圆柱的表面爬到P点的最短距离为 A、9cm B、10cm C、11cm D、12cm9. 如图, 中, ,将 沿DE翻折,使点A与点B重合,则CE的长为( )
A、9cm B、10cm C、11cm D、12cm9. 如图, 中, ,将 沿DE翻折,使点A与点B重合,则CE的长为( )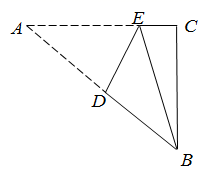 A、 B、2 C、 D、10. 如图, ,过点P作 且 ,得 ;再过点P,作 ,且 ,得 ;又过点 作 且 ,得 依此法继续作下去,得 ( )
A、 B、2 C、 D、10. 如图, ,过点P作 且 ,得 ;再过点P,作 ,且 ,得 ;又过点 作 且 ,得 依此法继续作下去,得 ( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如果 ,则x的取值范围是 .12. 若 有意义,则 .13. 若一个正整数的两个平方根为2m﹣6与3m+1,则这个数是 .14. 如图,一木杆在离地面9米处断裂,木杆顶部落在离木杆底端12米处,则木杆折断之前高米.
 15. 如图,以直角三角形的三边为边向外作三个正方形A、B、C . 若 , ,则 .
15. 如图,以直角三角形的三边为边向外作三个正方形A、B、C . 若 , ,则 . 16. 动手操作:在长方形纸片ABCD中,AB=6,AD=10.如图所示,折叠纸片,使点A落在BC边上的A′处,折痕为PQ , 当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点A′在BC边上可移动的最大距离为 .
16. 动手操作:在长方形纸片ABCD中,AB=6,AD=10.如图所示,折叠纸片,使点A落在BC边上的A′处,折痕为PQ , 当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点A′在BC边上可移动的最大距离为 .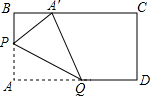
三、解答题
-
17. 计算:(1)、(2)、18.(1)、不使用计算器,估计 的近似值,(精确到0.01);(2)、已知 的整数部分为a , 小数部分为b . 求 的值.19. 如图,已知A、B、D在同一条直线上,且 ,
 (1)、求证: ;(2)、若设 , , ,试利用这个图形验证勾股定理.20. 如图,网格中每个小正方形的边长都为1.
(1)、求证: ;(2)、若设 , , ,试利用这个图形验证勾股定理.20. 如图,网格中每个小正方形的边长都为1. (1)、求四边形 的面积;(2)、求 的度数.21. 小明爸爸给小明出了一道题:如图,修公路 遇到一座山,于是要修一条隧道 .已知A , B , C在同一条直线上,为了在小山的两侧B , C同时施工,过点B作一直线m(在山的旁边经过),过点C作一直线l与m相交于D点,经测量 , , 米, 米.若施工队每天挖100米,求施工队几天能挖完?
(1)、求四边形 的面积;(2)、求 的度数.21. 小明爸爸给小明出了一道题:如图,修公路 遇到一座山,于是要修一条隧道 .已知A , B , C在同一条直线上,为了在小山的两侧B , C同时施工,过点B作一直线m(在山的旁边经过),过点C作一直线l与m相交于D点,经测量 , , 米, 米.若施工队每天挖100米,求施工队几天能挖完?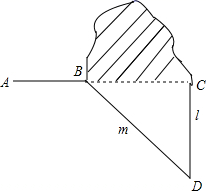 22.(1)、观察下列各式的特点:
22.(1)、观察下列各式的特点:,
> ,
,
,
…
根据以上规律可知: (填“>”“<”或“=”).
(2)、观察下列式子的化简过程:,
,
= ,
…
根据观察,请写出式子 (n≥2,且n是正整数)的化简过程.
(3)、根据上面(1)(2)得出的规律计算下面的算式: +| |+•••+| |.23. 如图,在△ABC中,AB=AC=5cm,BC=6cm,BD⊥AC交AC于点D . 动点P从点C出发,按C→A→B→C的路径运动,且速度为4cm/s,设出发时间为ts. (1)、求BC上的高;(2)、当CP⊥AB时,求t的值;(3)、当点P在BC边上运动时,若△CDP是等腰三角形,求出所有满足条件的t的值.
(1)、求BC上的高;(2)、当CP⊥AB时,求t的值;(3)、当点P在BC边上运动时,若△CDP是等腰三角形,求出所有满足条件的t的值.