浙江省湖州市长兴县2021-2022学年八年级上学期数学10月月考试卷
试卷更新日期:2021-10-28 类型:月考试卷
一、单选题
-
1. 下列各组数中,能够作为直角三角形的三边长的一组是( )A、1,2,3 B、2,3,4 C、4,5,6 D、3,4,52. 下面四个图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图, , , ,则 的度数为( )
3. 如图, , , ,则 的度数为( ) A、28 B、38 C、48 D、884. 下列说法中正确的是( )A、形状相同的两个三角形全等 B、面积相等的两个三角形全等 C、完全重合的两个三角形全等 D、周长相等的两个三角形全等5. 观察下列作图痕迹,所作线段 为 的角平分线的是( )A、
A、28 B、38 C、48 D、884. 下列说法中正确的是( )A、形状相同的两个三角形全等 B、面积相等的两个三角形全等 C、完全重合的两个三角形全等 D、周长相等的两个三角形全等5. 观察下列作图痕迹,所作线段 为 的角平分线的是( )A、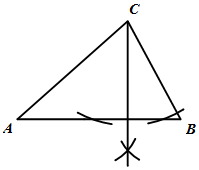 B、
B、 C、
C、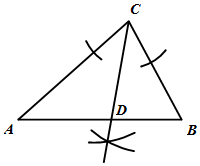 D、
D、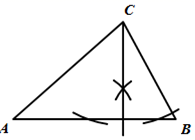 6. 如图,点E, F在直线AC上,DF=BE, ∠AFD=∠CEB,下列条件中不能判断△ADF≌△CBE的是( )
6. 如图,点E, F在直线AC上,DF=BE, ∠AFD=∠CEB,下列条件中不能判断△ADF≌△CBE的是( ) A、∠D=∠B B、AD=CB C、AE=CF D、AD// BC7. 如图,AO,BO分别平分 , ,且点O到AB的距离 , 的周长为28,则 的面积为( )
A、∠D=∠B B、AD=CB C、AE=CF D、AD// BC7. 如图,AO,BO分别平分 , ,且点O到AB的距离 , 的周长为28,则 的面积为( ) A、7 B、14 C、21 D、288. 如图,测河两岸A,B两点的距离时,先在AB的垂线BF上取C,D两点,使CD=BC,再过点D画出BF的垂线DE,当点A,C,E在同一直线上时,可证明△EDC≌△ABC,从而得到ED=AB,测得ED的长就是A,B的距离,判定△EDC≌△ABC的依据是:( )
A、7 B、14 C、21 D、288. 如图,测河两岸A,B两点的距离时,先在AB的垂线BF上取C,D两点,使CD=BC,再过点D画出BF的垂线DE,当点A,C,E在同一直线上时,可证明△EDC≌△ABC,从而得到ED=AB,测得ED的长就是A,B的距离,判定△EDC≌△ABC的依据是:( )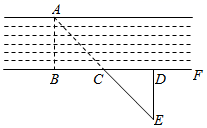 A、ASA B、SSS C、AAS D、SAS9. 如图,将一张正方形纸片经两次对折,并剪出一个菱形小洞后展开铺平,得到的图形是图中的哪一个( )
A、ASA B、SSS C、AAS D、SAS9. 如图,将一张正方形纸片经两次对折,并剪出一个菱形小洞后展开铺平,得到的图形是图中的哪一个( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 如图, 的面积是30cm2 , 以顶点A为圆心,适当长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,大于 的长为半径画弧,两弧交于点P,作射线AP,过点C作 于点D,连接BD,则 的面积是( )
10. 如图, 的面积是30cm2 , 以顶点A为圆心,适当长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,大于 的长为半径画弧,两弧交于点P,作射线AP,过点C作 于点D,连接BD,则 的面积是( ) A、15cm2 B、14cm2 C、13cm2 D、12cm2
A、15cm2 B、14cm2 C、13cm2 D、12cm2二、填空题
-
11. 在 中, , ,则 是三角形.(选填“锐角”、“直角”或“钝角”)12. 如图, ,直接根据“SAS”能说明图中三角形全等,你添加的条件是.
 13. 如图,DE,FG分别是AB,AC的垂直平分线.若 的周长为15,则 .
13. 如图,DE,FG分别是AB,AC的垂直平分线.若 的周长为15,则 . 14. 把命题“同角的余角相等”改写成“如果…那么…”的形式 .15. 一次数学测试,满分为100分.测试分数出来后,同桌的李华和吴珊同学把他俩的分数进行计算,李华说:我俩分数的和是160分,吴珊说:我俩分数的差是60分.那么,对于下列两个命题:①俩人的说法都是正确的;②至少有一人说错了;③俩人的说法都是错的.其中真命题是.(用序号填写)16. 如图, , 于A, 于B,且 ,P在线段AB上,Q在射线BD上.若 与△BQP全等,则 .
14. 把命题“同角的余角相等”改写成“如果…那么…”的形式 .15. 一次数学测试,满分为100分.测试分数出来后,同桌的李华和吴珊同学把他俩的分数进行计算,李华说:我俩分数的和是160分,吴珊说:我俩分数的差是60分.那么,对于下列两个命题:①俩人的说法都是正确的;②至少有一人说错了;③俩人的说法都是错的.其中真命题是.(用序号填写)16. 如图, , 于A, 于B,且 ,P在线段AB上,Q在射线BD上.若 与△BQP全等,则 .
三、解答题
-
17. 已知三条线段 , , ,以这三条线段为边能构成三角形吗?请说明理由.18. 如图,已知△ABC≌△EBD,
 (1)、若BE=6,BD=4,求线段AD的长;(2)、若∠E=30°,∠B=48°,求∠ACE的度数.19. 如图,已知 , .求证: .
(1)、若BE=6,BD=4,求线段AD的长;(2)、若∠E=30°,∠B=48°,求∠ACE的度数.19. 如图,已知 , .求证: .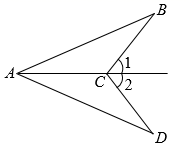 20. 如图,在 中, 是 的高线, 是 的角平分线,已知 .
20. 如图,在 中, 是 的高线, 是 的角平分线,已知 . (1)、求 的大小.(2)、若 是 的角平分线,求 的大小.21.
(1)、求 的大小.(2)、若 是 的角平分线,求 的大小.21. (1)、如图1,直线两侧有两点A,B,在直线上求一点C,使它到A、B两点的距离之和最小(作法不限,保留作图痕迹,不写作法).(2)、知识拓展:如图2,直线同侧有两点A,B,在直线上求一点C,使它到A,B两点的距离之和最小(作法不限,保留作图痕迹,不写作法).22. 如图,在 中,AD是角平分线,E,F分别为AC,AB上的点,且 .
(1)、如图1,直线两侧有两点A,B,在直线上求一点C,使它到A、B两点的距离之和最小(作法不限,保留作图痕迹,不写作法).(2)、知识拓展:如图2,直线同侧有两点A,B,在直线上求一点C,使它到A,B两点的距离之和最小(作法不限,保留作图痕迹,不写作法).22. 如图,在 中,AD是角平分线,E,F分别为AC,AB上的点,且 . (1)、求证: ;(2)、DE与DF有何数量关系?请说明理由.(可根据答卷图中的提示解答)23. 已知:如图①,在 和 中, , , ,AC,BD相交于点P.
(1)、求证: ;(2)、DE与DF有何数量关系?请说明理由.(可根据答卷图中的提示解答)23. 已知:如图①,在 和 中, , , ,AC,BD相交于点P. (1)、求证:① ;
(1)、求证:① ;② .
(2)、如图②,在 和 中, , , , , 相交于点P,AC与BD间有怎样的数量关系? 的度数为多少?24. 如图所示,在 中, , , ,D为AB的中点,点P在线段BC上由点B出发向点C运动,同时点Q在线段CA上由点C出发向点A运动,设运动时间为t(s). (1)、若点P与点Q的速度都是3cm/s,则经过多长时间 与 全等?请说明理由.(2)、若点P的速度比点Q的速度慢3cm/s,则经过多长时间 与 全等?请求出此时两点的速度.(3)、若点P、点Q分别以(2)中的速度同时从点B,C出发,都按逆时针方向沿 三边运动,则经过多长时间点P与点Q第一次相遇?相遇点在 的哪条边上?请求出相遇点到点B的距离.
(1)、若点P与点Q的速度都是3cm/s,则经过多长时间 与 全等?请说明理由.(2)、若点P的速度比点Q的速度慢3cm/s,则经过多长时间 与 全等?请求出此时两点的速度.(3)、若点P、点Q分别以(2)中的速度同时从点B,C出发,都按逆时针方向沿 三边运动,则经过多长时间点P与点Q第一次相遇?相遇点在 的哪条边上?请求出相遇点到点B的距离.