天津市九年级数学期中模拟卷
试卷更新日期:2021-10-28 类型:期中考试
一、单选题
-
1. 已知抛物线 ( 是常数, )经过点 ,当 时,与其对应的函数值 .有下列结论:① ;②关于x的方程 有两个不等的实数根;③ .其中,正确结论的个数是( )A、0 B、1 C、2 D、32. 下列图案中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 关于x的方程x(x﹣2)=2x根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断4. 如图,四边形 是正方形, 是坐标原点,对角线 , 分别位于 轴和 轴上,点 的坐标是 ,则正方形 的周长是( )
3. 关于x的方程x(x﹣2)=2x根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断4. 如图,四边形 是正方形, 是坐标原点,对角线 , 分别位于 轴和 轴上,点 的坐标是 ,则正方形 的周长是( ) A、 B、12 C、 D、5. 如图, 是 的内接三角形, 是 的直径,若 ,则 的度数是( )
A、 B、12 C、 D、5. 如图, 是 的内接三角形, 是 的直径,若 ,则 的度数是( )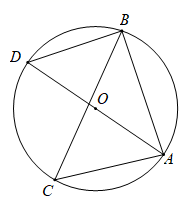 A、30° B、40° C、50° D、60°6. 正六边形的边心距为 ,这个正六边形的面积为( )A、12 B、 C、 D、7. 用一个圆心角为60°半径为6的扇形作一个圆锥的侧面,则这个圆锥的底面半径为( )A、1 B、2 C、3 D、48. 在Rt△ABC中,∠C=90°,AB=10.若以点C为圆心,CB为半径的圆恰好经过AB的中点D,则AC=()
A、30° B、40° C、50° D、60°6. 正六边形的边心距为 ,这个正六边形的面积为( )A、12 B、 C、 D、7. 用一个圆心角为60°半径为6的扇形作一个圆锥的侧面,则这个圆锥的底面半径为( )A、1 B、2 C、3 D、48. 在Rt△ABC中,∠C=90°,AB=10.若以点C为圆心,CB为半径的圆恰好经过AB的中点D,则AC=() A、5 B、 C、 D、69. 已知抛物线 ( , , 是常数, )经过点 ,其对称轴为直线 .有下列结论:① ;② ;③关于 的方程 有两个不等的实数根.其中,正确结论的个数是( )A、0 B、1 C、2 D、310. 已知抛物线 ( 是常数, )的顶点坐标是 ,与x轴的一个交点在点 和点 之间,其部分图象如图所示.有下列结论:① ;②关于x的方程 有两个不相等的实数根;③ .其中,正确结论的个数是( )
A、5 B、 C、 D、69. 已知抛物线 ( , , 是常数, )经过点 ,其对称轴为直线 .有下列结论:① ;② ;③关于 的方程 有两个不等的实数根.其中,正确结论的个数是( )A、0 B、1 C、2 D、310. 已知抛物线 ( 是常数, )的顶点坐标是 ,与x轴的一个交点在点 和点 之间,其部分图象如图所示.有下列结论:① ;②关于x的方程 有两个不相等的实数根;③ .其中,正确结论的个数是( )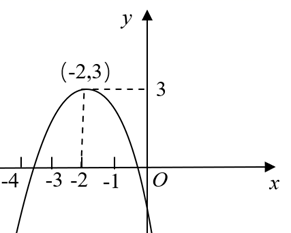 A、0 B、1 C、2 D、311. 如图是二次函数 图象的一部分,对称轴为 ,且经过点 .下列说法:① ;② ;③ ( 为任意实数).其中正确的个数为( )
A、0 B、1 C、2 D、311. 如图是二次函数 图象的一部分,对称轴为 ,且经过点 .下列说法:① ;② ;③ ( 为任意实数).其中正确的个数为( )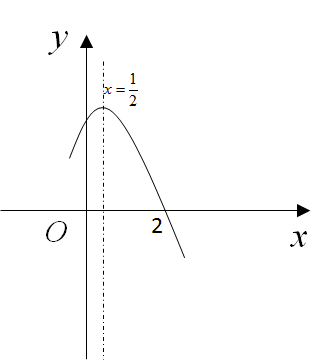 A、0 B、1 C、2 D、312. 下列语句中,正确的有( )
A、0 B、1 C、2 D、312. 下列语句中,正确的有( )①相等的圆心角所对的弧相等;
②平分弦的直径垂直于弦;
③长度相等的两条弧是等弧;
④经过圆心的每一条直线都是圆的对称轴.
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 若关于x的一元二次方程 有实数根,则m的取值范围是 .14. 若抛物线 与 轴没有交点,则 的取值范围为 .15. 已知点(2,6),(4,6)是抛物线 上的两点, 则这条抛物线的对称轴是 .16. 二次函数 向左、下各平移 个单位,所得的函数解析式 .17. 如图,将 绕点 逆时针旋转得到 .若 落到 边上, ,则 的度数为 .
 18. 如图,六边形ABCDEF是半径为2的⊙O的内接正六边形,则劣弧CD的长为 .
18. 如图,六边形ABCDEF是半径为2的⊙O的内接正六边形,则劣弧CD的长为 .
三、解答题
-
19. 如图,▱ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,求△DOE的周长.
 20.
20.如图,AB、CD是⊙O的直径,弦CE∥AB,弧CE的度数为40°,求∠AOC的度数.
 21. 已知 内接于 ,点D是 上一点.
21. 已知 内接于 ,点D是 上一点.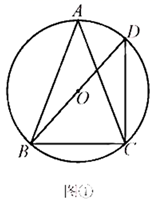

(Ⅰ)如图①,若 为 的直径,连接 ,求 和 的大小;
(Ⅱ)如图②,若 // ,连接 ,过点D作 的切线,与 的延长线交于点E,求 的大小.
22. 已知抛物线y=ax2+bx-1的图象经过点(-1,2),其对称轴为x=-1.求抛物线的解析式.23. 已知:抛物线y=-x2-6x+21.求:(1)、直接写出抛物线y=-x2-6x+21的顶点坐标;(2)、当x>2时,求y的取值范围.
