北师大版初中数学2021-2022学年九年级上学期期中测试模拟卷(二)
试卷更新日期:2021-10-27 类型:期中考试
一、单选题
-
1. 一元二次方程 ,配方后可形为( )A、 B、 C、 D、2. 小明计划到永州市体验民俗文化,想从“零陵渔鼓、瑶族长鼓舞、东安武术、舜帝祭典”四种民俗文化中任意选择两项,则小明选择体验“瑶族长鼓舞、舜帝祭典”的概率为( )A、 B、 C、 D、3. 如图, ABC中,点D、E分别在AB、AC上,且 ,下列结论正确的是( )
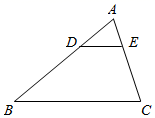 A、DE:BC=1:2 B、 ADE与 ABC的面积比为1:3 C、 ADE与 ABC的周长比为1:2 D、DE BC4. 如图,在菱形ABCD中,对角线AC,BD相交于点O,点E是CD中点,连接OE,则下列结论中不一定正确的是( )
A、DE:BC=1:2 B、 ADE与 ABC的面积比为1:3 C、 ADE与 ABC的周长比为1:2 D、DE BC4. 如图,在菱形ABCD中,对角线AC,BD相交于点O,点E是CD中点,连接OE,则下列结论中不一定正确的是( )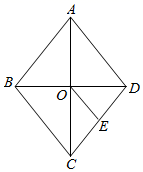 A、AB=AD B、OE AB C、∠DOE=∠DEO D、∠EOD=∠EDO5. 已知关于x的一元二次方程x2-kx+k-3=0的两个实数根分别为 ,且 ,则k的值是( )A、-2 B、2 C、-1 D、16. 如图,在 中, , 于点 , , , ,则 的长是( )
A、AB=AD B、OE AB C、∠DOE=∠DEO D、∠EOD=∠EDO5. 已知关于x的一元二次方程x2-kx+k-3=0的两个实数根分别为 ,且 ,则k的值是( )A、-2 B、2 C、-1 D、16. 如图,在 中, , 于点 , , , ,则 的长是( )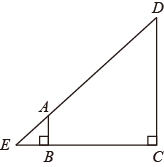 A、14 B、12.4 C、10.5 D、9.37. 如图,在平面直角坐标系中,将 以原点O为位似中心放大后得到 ,若 , ,则 与 的相似比是( )
A、14 B、12.4 C、10.5 D、9.37. 如图,在平面直角坐标系中,将 以原点O为位似中心放大后得到 ,若 , ,则 与 的相似比是( )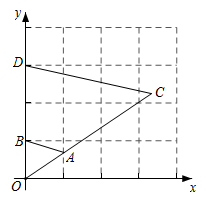 A、2:1 B、1:2 C、3:1 D、1:38. 某公司今年4月的营业额为2500万元,按计划第二季度的总营业额要达到9100万元,设该公司5、6两月的营业额的月平均增长率为x.根据题意列方程,则下列方程正确的是( )A、 B、 C、 D、9. 如图,矩形纸片 , ,点 , 分别在 , 上,把纸片如图沿 折叠,点 , 的对应点分别为 , ,连接 并延长交线段 于点 ,则 的值为( )
A、2:1 B、1:2 C、3:1 D、1:38. 某公司今年4月的营业额为2500万元,按计划第二季度的总营业额要达到9100万元,设该公司5、6两月的营业额的月平均增长率为x.根据题意列方程,则下列方程正确的是( )A、 B、 C、 D、9. 如图,矩形纸片 , ,点 , 分别在 , 上,把纸片如图沿 折叠,点 , 的对应点分别为 , ,连接 并延长交线段 于点 ,则 的值为( ) A、 B、 C、 D、10. 如图,在平行四边形ABCD中,∠ABC的平分线交AC于点E , 交AD于点F , 交CD的延长线于点G , 若AF=2FD , 则 的值为( )
A、 B、 C、 D、10. 如图,在平行四边形ABCD中,∠ABC的平分线交AC于点E , 交AD于点F , 交CD的延长线于点G , 若AF=2FD , 则 的值为( ) A、 B、 C、 D、11. 如图,在矩形纸片ABCD中,点E、F分别在矩形的边AB、AD上,将矩形纸片沿CE、CF折叠,点B落在H处,点D落在G处,点C、H、G恰好在同一直线上,若AB=6,AD=4,BE=2,则DF的长是( )
A、 B、 C、 D、11. 如图,在矩形纸片ABCD中,点E、F分别在矩形的边AB、AD上,将矩形纸片沿CE、CF折叠,点B落在H处,点D落在G处,点C、H、G恰好在同一直线上,若AB=6,AD=4,BE=2,则DF的长是( ) A、2 B、 C、 D、312. 如图,在正方形 中, ,E为对角线 上与A,C不重合的一个动点,过点E作 于点F, 于点G,连接 .下列结论:
A、2 B、 C、 D、312. 如图,在正方形 中, ,E为对角线 上与A,C不重合的一个动点,过点E作 于点F, 于点G,连接 .下列结论: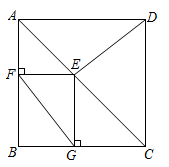
① ;② ;③ ;④ 的最小值为3.其中正确结论的个数有( )
A、1个 B、2个 C、3个 D、4个二、填空题
-
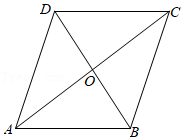
13. 如图,已知四边形ABCD是平行四边形,从①AB=AD,②AC=BD,③∠ABC=∠ADC中选择一个作为条件,补充后使四边形ABCD成为菱形,则其选择是 (限填序号).
 14. 两个人做游戏:每个人都从-1,0,1这三个整数中随机选择一个写在纸上,则两人所写整数的绝对值相等的概率为 .15. 如图是一架梯子的示意图,其中AA1∥BB1∥CC1∥DD1 , 且AB=BC=CD.为使其更稳固,在A,D1间加绑一条安全绳(线段AD1)量得AE=0.4m,则AD1=m.
14. 两个人做游戏:每个人都从-1,0,1这三个整数中随机选择一个写在纸上,则两人所写整数的绝对值相等的概率为 .15. 如图是一架梯子的示意图,其中AA1∥BB1∥CC1∥DD1 , 且AB=BC=CD.为使其更稳固,在A,D1间加绑一条安全绳(线段AD1)量得AE=0.4m,则AD1=m. 16. 如图,为了测量山坡的护坡石坝高,把一根长为 的竹竿 斜靠在石坝旁,量出竿上 长为 时,它离地面的高度 为 ,则坝高 为 .
16. 如图,为了测量山坡的护坡石坝高,把一根长为 的竹竿 斜靠在石坝旁,量出竿上 长为 时,它离地面的高度 为 ,则坝高 为 . 17. 如图,在 中, ,矩形 的顶点D、E在 上,点F、G分别在 、 上,若 , ,且 ,则 的长为.
17. 如图,在 中, ,矩形 的顶点D、E在 上,点F、G分别在 、 上,若 , ,且 ,则 的长为.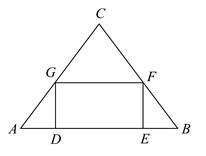 18. 如图,将 绕点A逆时针旋转到 的位置,使点 落在 上, 与 交于点E,若 ,则 的长为.
18. 如图,将 绕点A逆时针旋转到 的位置,使点 落在 上, 与 交于点E,若 ,则 的长为.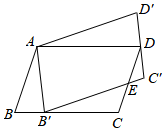
三、解答题
-
19. 用配方法解方程 .20. 解方程:3x(x-1)=2-2x21. 为庆祝中国共产党建党100周年,某校拟举办主题为“学党史跟党走”的知识竞赛活动.某年级在一班和二班进行了预赛,两个班参加比赛的人数相同,成绩分为A、B、C、D四个等级,其等级对应的分值分别为100分、90分、80分、70分,将这两个班学生的最后等级成绩分析整理绘制成了如下的统计图.
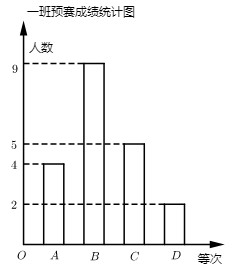
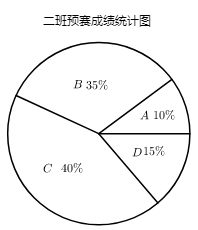 (1)、这次预赛中二班成绩在B等及以上的人数是多少?(2)、分别计算这次预赛中一班成绩的平均数和二班成绩的中位数;(3)、已知一班成绩A等的4人中有两个男生和2个女生,二班成绩A等的都是女生,年级要求从这两个班A等的学生中随机选2人参加学校比赛,若每个学生被抽取的可能性相等,求抽取的2人中至少有1个男生的概率.22. 若x1 , x2是关于x的一元二次方程ax2+bx+c=0的两个根,则x1+x2=﹣ ,x1•x2= .现已知一元二次方程px2+2x+q=0的两根分别为m,n.(1)、若m=2,n=﹣4,求p,q的值;(2)、若p=3,q=﹣1,求m+mn+n的值.23. 如图,在 和 中, , .
(1)、这次预赛中二班成绩在B等及以上的人数是多少?(2)、分别计算这次预赛中一班成绩的平均数和二班成绩的中位数;(3)、已知一班成绩A等的4人中有两个男生和2个女生,二班成绩A等的都是女生,年级要求从这两个班A等的学生中随机选2人参加学校比赛,若每个学生被抽取的可能性相等,求抽取的2人中至少有1个男生的概率.22. 若x1 , x2是关于x的一元二次方程ax2+bx+c=0的两个根,则x1+x2=﹣ ,x1•x2= .现已知一元二次方程px2+2x+q=0的两根分别为m,n.(1)、若m=2,n=﹣4,求p,q的值;(2)、若p=3,q=﹣1,求m+mn+n的值.23. 如图,在 和 中, , . (1)、求证: ;(2)、若 , ,求 的长.24. 定义:若四边形有一组对角互补,一组邻边相等,且相等邻边的夹角为直角,像这样的图形称为“直角等邻对补”四边形,简称“直等补”四边形,根据以上定义,解决下列问题:
(1)、求证: ;(2)、若 , ,求 的长.24. 定义:若四边形有一组对角互补,一组邻边相等,且相等邻边的夹角为直角,像这样的图形称为“直角等邻对补”四边形,简称“直等补”四边形,根据以上定义,解决下列问题: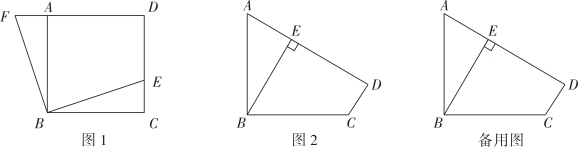 (1)、如图1,正方形 中,E是 上的点,将 绕B点旋转,使 与 重合,此时点E的对应点F在 的延长线上,则四边形 为“直等补”四边形,为什么?(2)、如图2,已知四边形 是“直等补”四边形, , , ,点 到直线 的距离为 .
(1)、如图1,正方形 中,E是 上的点,将 绕B点旋转,使 与 重合,此时点E的对应点F在 的延长线上,则四边形 为“直等补”四边形,为什么?(2)、如图2,已知四边形 是“直等补”四边形, , , ,点 到直线 的距离为 .①求 的长.
②若M、N分别是 、 边上的动点,求 周长的最小值.
25. 如图,在菱形ABCD中, , ,点E为边AB上一个动点,延长BA到点F , 使 ,且CF、DE相交于点G (1)、当点E运动到AB中点时,证明:四边形DFEC是平行四边形;(2)、当 时,求AE的长;(3)、当点E从点A开始向右运动到点B时,求点G运动路径的长度.26. 如图,
(1)、当点E运动到AB中点时,证明:四边形DFEC是平行四边形;(2)、当 时,求AE的长;(3)、当点E从点A开始向右运动到点B时,求点G运动路径的长度.26. 如图, (1)、【推理】
(1)、【推理】
如图1,在正方形ABCD中,点E是CD上一动点,将正方形沿着BE折叠,点C落在点F处,连结BE,CF,延长CF交AD于点G. 求证: .(2)、【运用】
如图2,在(推理)条件下,延长BF交AD于点H.若 , ,求线段DE的长.(3)、【拓展】
将正方形改成矩形,同样沿着BE折叠,连结CF,延长CF,BF交直线AD于G,两点,若 , ,求 的值(用含k的代数式表示).