山东省烟台市2020-2021学年高二上学期数学期末考试试卷
试卷更新日期:2021-10-27 类型:期末考试
一、单选题
-
1. 数列2,-4,6,-8,…的通项公式可能是( )A、 B、 C、 D、2. 若抛物线 过点 ,则该抛物线的焦点坐标为( )A、 B、 C、 D、3. 与双曲线 有公共焦点且离心率为 的椭圆的标准方程为( )A、 B、 C、 D、4. 传说古希腊毕达哥拉斯学派的数学家用沙粒和小石子研究数.他们根据沙粒和石子所排列的形状把数分成许多类,如:三角形数1,3,6,10,…;正方形数1,4,9,16,…;等等.如图所示为五边形数,将五边形数按从小到大的顺序排列成数列,则此数列的第7项为( )
 A、35 B、51 C、70 D、925. 设 , 是椭圆 的焦点,若椭圆 上存在一点 满足 ,则 的取值范围是( )A、 B、 C、 D、6. 已知数列 满足 , ,则 ( )A、 B、 C、 D、27. 如图是一水平放置的青花瓷.它的外形为单叶双曲面,可看成是双曲线的一部分绕其虚轴旋转所形成的曲面,且其外形上下对称.花瓶的最小直径为 ,瓶口直径为 ,瓶高为 ,则该双曲线的虚轴长为( )
A、35 B、51 C、70 D、925. 设 , 是椭圆 的焦点,若椭圆 上存在一点 满足 ,则 的取值范围是( )A、 B、 C、 D、6. 已知数列 满足 , ,则 ( )A、 B、 C、 D、27. 如图是一水平放置的青花瓷.它的外形为单叶双曲面,可看成是双曲线的一部分绕其虚轴旋转所形成的曲面,且其外形上下对称.花瓶的最小直径为 ,瓶口直径为 ,瓶高为 ,则该双曲线的虚轴长为( )
 A、 B、 C、 D、458. 已知数列 的通项公式为 ,将数列 中的整数从小到大排列得到新数列 ,则 的前100项和为( )A、9900 B、10200 C、10000 D、11000
A、 B、 C、 D、458. 已知数列 的通项公式为 ,将数列 中的整数从小到大排列得到新数列 ,则 的前100项和为( )A、9900 B、10200 C、10000 D、11000二、多选题
-
9. 下列命题中正确的是( )A、双曲线 与直线 有且只有一个公共点 B、平面内满足 的动点 的轨迹为双曲线 C、若方程 表示焦点在 轴上的双曲线,则 D、过给定圆上一定点 作圆的动弦 ,则弦 的中点 的轨迹为椭圆10. 若数列 满足 , , ,则称 为斐波那契数列.记数列 的前 项和为 ,则( )A、 B、 C、 D、11. 如图,椭圆的中心在坐标原点,焦点在 轴上, , , 为椭圆的顶点, 为右焦点,延长 与 交于点 ,若 为钝角,则该椭圆的离心率可能为( )
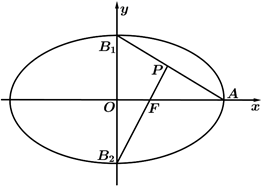 A、 B、 C、 D、12. 已知数列1, ,1, , ,1, , , ,1,…,则( )A、数列的第 项均为1 B、 是数列的第90项 C、数列前50项和为28 D、数列前50项和为
A、 B、 C、 D、12. 已知数列1, ,1, , ,1, , , ,1,…,则( )A、数列的第 项均为1 B、 是数列的第90项 C、数列前50项和为28 D、数列前50项和为三、填空题
-
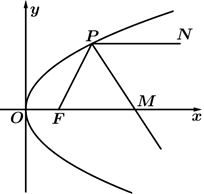
13. 已知等差数列 的前 项和为 , , ,则 的最大值为 .14. 已知椭圆 的一个焦点与抛物线 的焦点重合,过点 且斜率为 的直线交椭圆 于 , 两点,若 是线段 的中点,则椭圆 的方程为 .15. 已知 为等比数列 的前 项和, , ,则 的值为 .16. 汽车前照灯的反射镜为一个抛物面.它由抛物线沿它的对称轴旋转一周形成.通常前照灯主要是由灯泡、反射镜和透镜三部分组成,其中灯泡位于抛物面的焦点上.由灯泡发出的光经抛物面反射镜反射后形成平行光束,再经过进镜的折射等作用达到照亮路面的效果.如图,从灯泡发出的光线 经抛物线 反射后,沿 平行射出, 的角平分线 所在的直线方程为 ,则抛物线方程为 .
四、解答题
-
17. 从条件① ,② ,③ 任选一个补充在下面问题中,并解答.
问题:已知数列 的各项均为正数, 为等比数列, , , ▲ , 求数列 的前 项和 .如果选择多个条件分别解答,按第一个解答计分.
18. 动点 与定点 的距离和 到定直线 的距离的比是常数 .(1)、求动点 的轨迹方程;(2)、设 ,点 为 轨迹上一点,且 ,求 的面积.19. 在购买住房、轿车等商品时,一次性付款可能会超出一些买主的支付能力,贷款消费不失为一种可行的选择,但是也要量入为出,理智消费.某家庭计划在2021年元旦从某银行贷款10万元购置一辆轿车,贷款时间为18个月.该银行现提供了两种可选择的还款方案:方案一是以月利率0.4%的复利计息,每月底还款,每次还款金额相同;方案二是以季度利率1.2%的复利计息,每季度末还款,每次还款金额相同.(注:复利是指把前一期的利息与本金之和作为本金,再计算下一期的利息.)(1)、分别计算选择方案一、方案二时,该家庭每次还款金额为多少万元?(结果精确到小数点后三位,参考数据: , .)(2)、从每季度还款金额较少的角度看,该家庭应选择哪种方案?说明理由.20. 已知抛物线 的方程为 ,点 ,过点 的直线交抛物线于 , 两点.(1)、 是否为定值?若是,求出该定值;若不是,说明理由;(2)、若点 是直线 上的动点,且 ,求 面积的最小值.