苏科版初中数学2021-2022学年九年级上学期期中测试模拟卷
试卷更新日期:2021-10-27 类型:期中考试
一、单选题
-
1. 如图,点 在 上, , ,则 等于( )
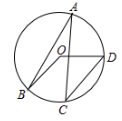 A、 B、 C、 D、2. 如图,AB是⊙O的直径,点C和点D是⊙O上位于直径AB两侧的点,连接AC,AD,BD,CD,若⊙O的半径是13,BD=24,则sin∠ACD的值是( )
A、 B、 C、 D、2. 如图,AB是⊙O的直径,点C和点D是⊙O上位于直径AB两侧的点,连接AC,AD,BD,CD,若⊙O的半径是13,BD=24,则sin∠ACD的值是( ) A、 B、 C、 D、3. 二次函数y=-2x2+4x+1的对称轴和顶点坐标分别是( )A、x=-1,(1,3) B、x=-1,(-1,3) C、x=1,(-1,3) D、x=1,(1,3)4. 二次函数y=ax2+bx+c(a≠0)的部分图象如图4所示,图象过点(-4,0),对称轴为直线x=-1。有下列结论:①abc>0;②2a-b=0;③一元二次方程ax2+bx+c=0的解是x1=-4,x2=1;④当y>0时,-4< x< 2。其中正确的结论有( )
A、 B、 C、 D、3. 二次函数y=-2x2+4x+1的对称轴和顶点坐标分别是( )A、x=-1,(1,3) B、x=-1,(-1,3) C、x=1,(-1,3) D、x=1,(1,3)4. 二次函数y=ax2+bx+c(a≠0)的部分图象如图4所示,图象过点(-4,0),对称轴为直线x=-1。有下列结论:①abc>0;②2a-b=0;③一元二次方程ax2+bx+c=0的解是x1=-4,x2=1;④当y>0时,-4< x< 2。其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个5. 已知二次函数 的图象如图所示,有下列结论:① ;② >0;③ ;④不等式 <0的解集为1≤x<3,正确的结论个数是( )
A、1个 B、2个 C、3个 D、4个5. 已知二次函数 的图象如图所示,有下列结论:① ;② >0;③ ;④不等式 <0的解集为1≤x<3,正确的结论个数是( )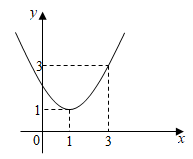 A、1 B、2 C、3 D、46. 若关于 的方程 是关于 的一元二次方程,则m的取值为( )A、 B、 C、 D、7. 如图,已知弧AB的半径为5,所对的弦AB长为8,点P是弧AB的中点,将弧AB绕点A逆时针旋转90°后得到弧AB′则在该旋转过程中,点P的运动路径长是( )
A、1 B、2 C、3 D、46. 若关于 的方程 是关于 的一元二次方程,则m的取值为( )A、 B、 C、 D、7. 如图,已知弧AB的半径为5,所对的弦AB长为8,点P是弧AB的中点,将弧AB绕点A逆时针旋转90°后得到弧AB′则在该旋转过程中,点P的运动路径长是( ) A、 π B、 π C、2 π D、2π8. 关于x的方程 (p为常数)的根的情况,下列结论中正确的是( )A、两个正根 B、两个负根 C、一个正根,一个负根 D、根的符号与p的值有关9. 关于x的一元二次方程(m-2)x2+3x-1=0有实数根,那么m的取值范围是( )A、m≤ B、m≥ 且m≠2 C、m≤ 且m≠﹣2 D、m≥10. 若(a2+b2﹣3)2=25,则a2+b2=( )A、8或﹣2 B、﹣2 C、8 D、2或﹣8
A、 π B、 π C、2 π D、2π8. 关于x的方程 (p为常数)的根的情况,下列结论中正确的是( )A、两个正根 B、两个负根 C、一个正根,一个负根 D、根的符号与p的值有关9. 关于x的一元二次方程(m-2)x2+3x-1=0有实数根,那么m的取值范围是( )A、m≤ B、m≥ 且m≠2 C、m≤ 且m≠﹣2 D、m≥10. 若(a2+b2﹣3)2=25,则a2+b2=( )A、8或﹣2 B、﹣2 C、8 D、2或﹣8二、填空题
-
11. 已知关于x的一元二次方程 没有实数根,即实数c的取值范围是 .12. 为把我市创建成全国文明城市,某社区积极响应市政府号召,准备在 一块正方形的空地上划出部分区域栽种鲜花,如图中的阴影“┛”带,鲜花带一边宽1m.另一边宽2m,剩余空地的面积为18m2 , 求原正方形空地的边长 m,可列方程为.
 13. 如图,在 中, , , .以点 为圆心, 长为半径画弧,分别交 , 于点 , ,则图中阴影部分的面积为(结果保留 ).
13. 如图,在 中, , , .以点 为圆心, 长为半径画弧,分别交 , 于点 , ,则图中阴影部分的面积为(结果保留 ).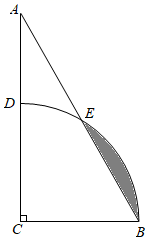 14. 如图,在 中, ,以AD为直径的 与BC相切于点E , 连接OC . 若 ,则 的周长为 .
14. 如图,在 中, ,以AD为直径的 与BC相切于点E , 连接OC . 若 ,则 的周长为 . 15. 用配方法解方程 ,将方程变为 的形式,则 .16. 如图,抛物线 ( )与 轴交于点 ,与 轴交于 , 两点,其中点 的坐标为 ,抛物线的对称轴交 轴于点 , ,并与抛物线的对称轴交于点 .现有下列结论:① ;② ;③ ;④ .其中所有正确结论的序号是 .
15. 用配方法解方程 ,将方程变为 的形式,则 .16. 如图,抛物线 ( )与 轴交于点 ,与 轴交于 , 两点,其中点 的坐标为 ,抛物线的对称轴交 轴于点 , ,并与抛物线的对称轴交于点 .现有下列结论:① ;② ;③ ;④ .其中所有正确结论的序号是 .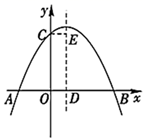 17. 如图,A是⊙O上一点,BC是直径,AC=2,AB=4,点D在⊙O上且平分 ,则DC的长为.
17. 如图,A是⊙O上一点,BC是直径,AC=2,AB=4,点D在⊙O上且平分 ,则DC的长为.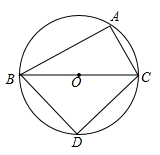 18. 小明设计了一个魔术盒,当任意实数对(a,b)进入其中时,会得到一个新的实数a2+2b-3.例如把(2,-5)放入其中就会得到22+2×(-5)-3=-9.现将实数对(m,-3m)放入其中,得到实数4,则m=.
18. 小明设计了一个魔术盒,当任意实数对(a,b)进入其中时,会得到一个新的实数a2+2b-3.例如把(2,-5)放入其中就会得到22+2×(-5)-3=-9.现将实数对(m,-3m)放入其中,得到实数4,则m=.三、解答题
-
19. 解下列一元二次方程:(1)、 ;(2)、 .20. 某商家销售一款商品,该商品的进价为每件80元,现在的售价为每件145元,每天可销售40件商场规定每销售一件需支付给商场管理费5元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件若每件商品降价 元,每天的利润为 元,请完成以下问题的解答.(1)、用含 的式子表示:①每件商品的售价为元;②每天的销售量为件;(2)、求出 与 之间的函数关系式,并求出售价为多少时利润最大?最大利润是多少元?21. 宁波某公司经销一种绿茶,每千克成本为 元.市场调查发现,在一段时间内,销售量 (千克)随销售单价 (元/千克)的变化而变化,具体关系式为: .设这种绿茶在这段时间内的销售利润为 (元),解答下列问题:(1)、求 与 的关系式;(2)、当销售单价 取何值时,销售利润 的值最大,最大值为多少?(3)、如果物价部门规定这种绿茶的销售单价不得高于 元/千克,公司想要在这段时间内获得 元的销售利润,销售单价应定为多少元?22. 如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a。将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD。
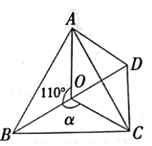 (1)、证明:△COD是等边三角形;(2)、当a=150°时,试判断△AOD的形状,并说明理由(3)、探究:当a为多少度时,△AOD是等腰三角形?23. 如图①,∠QPN的顶点P在正方形ABCD两条对角线的交点处,∠QPN=α,将∠QPN绕点P旋转,旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C,D不重合).
(1)、证明:△COD是等边三角形;(2)、当a=150°时,试判断△AOD的形状,并说明理由(3)、探究:当a为多少度时,△AOD是等腰三角形?23. 如图①,∠QPN的顶点P在正方形ABCD两条对角线的交点处,∠QPN=α,将∠QPN绕点P旋转,旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C,D不重合). (1)、如图①,当α=90°时,DE,DF,AD之间满足的数量关系是;(2)、如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为DE+DF= AD,请给出证明;(3)、在(2)的条件下,若旋转过程中∠QPN的边PQ与射线AD交于点E,其他条件不变,探究在整个运动变化过程中,DE,DF,AD之间满足的数量关系,直接写出结论,不用加以证明.24. 学校实施新课程改革以来,学生的学习能力有了很大提高,陈老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分成四类( :特别好, :好, :一般, :较差).并将调查结果绘制成以下两幅不完整的统计图,请根据统计图解答下列问题:
(1)、如图①,当α=90°时,DE,DF,AD之间满足的数量关系是;(2)、如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为DE+DF= AD,请给出证明;(3)、在(2)的条件下,若旋转过程中∠QPN的边PQ与射线AD交于点E,其他条件不变,探究在整个运动变化过程中,DE,DF,AD之间满足的数量关系,直接写出结论,不用加以证明.24. 学校实施新课程改革以来,学生的学习能力有了很大提高,陈老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分成四类( :特别好, :好, :一般, :较差).并将调查结果绘制成以下两幅不完整的统计图,请根据统计图解答下列问题:
 (1)、本次调查中,陈老师一共调查了名学生;(2)、将条形统计图补充完整;求扇形统计图中 类学生所对应的圆心角;(3)、为了共同进步,陈老师从被调查的 类和 类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.
(1)、本次调查中,陈老师一共调查了名学生;(2)、将条形统计图补充完整;求扇形统计图中 类学生所对应的圆心角;(3)、为了共同进步,陈老师从被调查的 类和 类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.