山东省菏泽市2020-2021学年高二上学期数学期末考试试卷

试卷更新日期：2021-10-27 类型：期末考试

进入出卷网下载

一、单选题

1. -401是等差数列-5，-9，-13……，的第（）项．

A、98 B、99 C、100 D、101

查看试题解析
2. “ $a = - 1$ ”是“直线 $x + a y + 6 = 0$ 和直线 $(a - 2) x + 3 y + 2 a = 0$ 平行”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
3. 在正四面体 $P - A B C$ 中，棱长为1，且D为棱 $A B$ 的中点，则 $\vec{P C} \cdot \vec{P D}$ 的值为（）

A、 $- \frac{1}{4}$ B、 $\frac{1}{4}$ C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
4. 日常生活的饮用水通常是经过净化的，随着水的纯净度的提高，所需净化费用不断增加．已知将 $1t$ 水净化到纯净度为 $x %$ 时所需费用（单位：元）为 $c (x) = \frac{5284}{100 - x} (80 < x < 100)$ ．设将 $1t$ 水净化到纯净度为92%，98%时，所需净化费用的瞬时变化率分别为 $t_{1} ， t_{2}$ ，则 $\frac{t_{2}}{t_{1}} =$ （）

A、 $\frac{1}{16}$ B、16 C、 $\frac{1}{25}$ D、25

查看试题解析
5. 已知双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ $(a > 0 ， b > 0)$ 的离心率为 $\sqrt{2}$ ，则点 $(4 ， 0)$ 到 $C$ 的渐近线的距离为（）

A、 $\sqrt{2}$ B、 $2$ C、 $\frac{3 \sqrt{2}}{2}$ D、 $2 \sqrt{2}$

查看试题解析
6. 如图，在菱形 $A B C D$ 中， $A B = 2 ， ∠ D A B = 60 °$ ，E是 $A B$ 的中点，将 $△ A D E$ 沿直线 $D E$ 翻折至的位置 $△ A_{1} D E$ ，使得面 $A_{1} D E ⊥$ 面 $B C D E$ ，则点 $A_{1}$ 到平面 $B C D E$ 的距离为（）

A、1 B、2 C、 $\frac{\sqrt{3}}{2}$ D、 $\sqrt{3}$

查看试题解析
7. 若函数 $e^{x} f (x)$ （ $e = 2.718 \cdot \cdot \cdot$ ，e为自然对数的底数）在 $f (x)$ 的定义域上单调递增，则称函数 $f (x)$ 具有M性质，下列函数具有M性质的为（）

A、 $f (x) = x^{2} - 1$ B、 $f (x) = x^{3}$ C、 $f (x) = \sin x$ D、 $f (x) = \ln x$

查看试题解析
8. 某养猪场2021年年初猪的存栏数1200，预计以后每年存栏数的增长率为8%，且在每年年底卖出100头．设该养猪场从今年起每年年初的计划存栏数依次为 $a_{1} ， a_{2} ， a_{3} ， \dots$ ．则2035年年底存栏头数为（参考数据： ${1.08}^{14} \approx 2.9 ， {1.08}^{15} \approx 3.2 ， {1.08}^{16} \approx 3.4$ ）（）

A、1005 B、1080 C、1090 D、1105

查看试题解析

二、多选题

9. 已知直线 $l ： m x - (2 - m) y + 1 - m = 0$ ，圆 $C ： x^{2} + y^{2} - 2 x = 0$ ，则下列结论正确的是（）

A、直线l与圆C恒有两个公共点 B、圆心C到直线l的最大距离是 $\sqrt{2}$ C、存在一个m值，使直线l经过圆心C D、当 $m = 1$ 时，圆C与圆 $x^{2} + {(y - 1)}^{2} = 1$ 关于直线l对称

查看试题解析
10. 某地2020年12月20日至2021年1月23日的新冠肺炎每日确诊病例变化曲线如下图所示．

若该地这段时间的新冠肺炎每日的确诊人数按日期先后顺序构成数列 ${a_{n}}$ ， ${a_{n}}$ 的前n项和为 $S_{n}$ ，则下列说法正确的是（）

A、数列 ${a_{n}}$ 是递增数列 B、数列 ${S_{n}}$ 不是递增数列 C、数列 ${a_{n}}$ 的最大项为 $a_{11}$ D、数列 ${S_{n}}$ 的最大项为 $S_{11}$

查看试题解析
11. 设函数 $f (x) = x (x - 1) (x - a)$ ，则下列结论正确的是（）

A、当 $a = - 4$ 时，函数 $f (x)$ 在 $[- 1 ， \frac{1}{2}]$ 上的平均变化率为 $- \frac{19}{4}$ B、当 $a = 1$ 时，函数 $f (x)$ 的图象与直线 $y = - 1$ 有1个交点 C、当 $a = 2$ 时，函数 $f (x)$ 的图象关于点 $(0 ， 1)$ 中心对称 D、若函数 $f (x)$ 有两个不同的极值点 $x_{1} ， x_{2}$ ，则当 $a \geq 2$ 时， $f (x_{1}) + f (x_{2}) \leq 0$

查看试题解析
12. 已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左右焦点分别为 $F_{1} ， F_{2}$ ，其长轴长是短轴长的 $\frac{5}{4}$ ，若点P是椭圆上不与 $F_{1} ， F_{2}$ ，共线的任意点，且 $△ P F_{1} F_{2}$ 的周长为16，则下列结论正确的是（）

A、C的方程为 $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$ B、C的离心率为 $\frac{4}{5}$ C、双曲线 $\frac{x^{2}}{5} - \frac{y^{2}}{4} = 1$ 的渐近线与椭圆C在第一象限内的交点为 $(\frac{10}{3} ， \frac{4}{3} \sqrt{5})$ D、点Q是圆 $x^{2} + y^{2} = 25$ 上一点，点A，B是C的左右顶点（Q不与A，B重合），设直线 $P B$ ， $Q B$ 的斜率分别为 $k_{1} ， k_{2}$ ，若A，P，Q三点共线则 $25 k_{1} = 16 k_{2}$

查看试题解析

三、填空题

13. 若点 $P (\frac{π}{2} ， y_{0})$ 是曲线 $y = \cos (\frac{2}{3} x + \frac{π}{6})$ 上一点，直线l为点P处的切线，则直线l的方程为．

查看试题解析
14. 两圆 ${(x + 1)}^{2} + y^{2} = 9$ 和 $x^{2} + y^{2} + 4 x - 4 y = 0$ 相交于两点M，N，则线段 $M N$ 的长为．

查看试题解析
15. 正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱 $A B$ 和 $A_{1} D_{1}$ 的中点分别为E，F，则直线 $E F$ 与平面 $A A_{1} D_{1} D$ 所成角的余弦值为．

查看试题解析
16. 已知抛物线 $C ： y^{2} = 4 x$ 的焦点F与双曲线 $\frac{λ x^{2}}{3} - λ y^{2} = 1 (λ > 0)$ 的右焦点相同，则双曲线的方程为，过点F分别作两条直线 $l_{1} ， l_{2}$ ，直线 $l_{1}$ 与抛物线C交于A，B两点，直线 $l_{2}$ 与抛物线C交于D，E两点，若 $l_{1}$ 与 $l_{2}$ 的斜率的平方和为1，则 $| A B | + | D E |$ 的最小值为．

查看试题解析

四、解答题

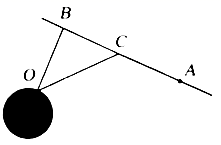
17. 已知圆C的圆心在直线 $y = x$ 上，圆心到x轴的距离为2，且截y轴所得弦长为 $2 \sqrt{14}$ ．

(1)、求圆C的方程；

(2)、若圆C上至少有三个不同的点到直线 $l ： y = k x$ 的距离为 $2 \sqrt{2}$ ，求实数k的取值范围．

查看试题解析
18. 已知数列 ${a_{n}}$ 的前n项和是 $A_{n}$ ，数列 ${b_{n}}$ 的前n项和是 $B_{n}$ ，若 $a_{1} = 1 ， a_{n + 1} = 2 a_{n} + 1 ， n \in N^{*}$ ，再从三个条件：① $B_{n} = - n^{2} + 21 n$ ；② $B_{n + 1} - b_{n} = B_{n} - 2$ ， $b_{1} = 20$ ；③ $b_{n} = 22 - 2 \log_{2} (a_{n} + 1)$ ，中任选一组作为已知条件，完成下面问题的解答（如果选择多组条件解答，则以选择第一组解答记分）．

(1)、求数列 ${a_{n}}$ ， ${b_{n}}$ 的通项公式；

(2)、定义： $a * b = {\begin{array}{l} a ， a \leq b \\ b ， a > b \end{array}$ ，记 $c_{n} = a_{n} * b_{n}$ ，求数列 ${c_{n}}$ 的前n项和 $T_{n}$ ．

查看试题解析
19. 如图，一海岛O，离岸边最近点B的距离是 $120km$ ，在岸边距点B $300km$ 的点A处有一批药品要尽快送达海岛．已知A和B之间有一条快速路，现要用海陆联运的方式运送这批药品，若汽车时速为 $100km$ ，快艇时速为 $50km$ ．设点C到点B的距离为x．（参考数据： $\sqrt{3} \approx 1.7$ ．）

(1)、写出运输时间 $t (x)$ 关于x的函数；

(2)、当点C选在何处时运输时间最短？

查看试题解析
20. 如图，在四棱锥 $P - A B C D$ 中， $P A ⊥$ 底面 $A B C D$ ， $A D / / B C ， A B = A D = A C = 3 ， B C = 4$ ，M为线段 $A D$ 上一点， $\vec{A M} = 2 \vec{M D}$ ，N为 $P C$ 的中点．

(1)、证明： $M N //$ 平面 $P A B$ ；

(2)、若平面 $A M N$ 与平面 $P A D$ 所成的锐二面角的正弦值为 $\frac{\sqrt{5}}{3}$ ，求直线 $M N$ 与直线 $P A$ 所成角的余弦值．

查看试题解析
21. 已知P是圆 $F_{1} ： {(x + 1)}^{2} + y^{2} = 16$ 上任意一点， $F_{2} (1 ， 0)$ ，线段 $P F_{2}$ 的垂直平分线与半径 $P F_{1}$ 交于点Q，当点P在圆 $F_{1}$ 上运动时，记点Q的轨迹为曲线C．

(1)、求曲线C的方程；

(2)、记曲线C与x轴交于A，B两点，在直线 $x = 4$ 上任取一点 $T (4 ， m) (m \neq 0)$ ，直线 $T A$ ， $T B$ 分别交曲线C于M，N两点，判断直线 $M N$ 是否过定点，若是，求出该定点的坐标；若不是，请说明理由．

查看试题解析
22. 已知函数 $f (x) = x^{2} + a x + 2 \ln x$ （a为常数）．

(1)、当 $a \leq 4$ 时，讨论函数 $f (x)$ 的单调性；

(2)、若 $f (x)$ 存在两个极值点 $x_{1} ， x_{2}$ ，且 $| x_{1} - x_{2} | \leq \frac{3}{2}$ ，证明 $| f (x_{1}) - f (x_{2}) | \leq \frac{15}{4} - 4 \ln 2$ ．

查看试题解析