苏科版初中数学2021-2022学年八年级上学期期中测试模拟卷
试卷更新日期:2021-10-26 类型:期中考试
一、单选题
-
1. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若下列各组值代表线段的长度,以它们为边不能构成三角形的是( )A、3,8,4 B、4,9,6 C、15,20,8 D、9,15,83. 如果等腰三角形的两边长分别为3和6,那么它的周长为( )A、9 B、12 C、15 D、12或154. 如图,点B,E,C,F在同一条直线上,已知 , ,添加下列条件还不能判定的 是( )
2. 若下列各组值代表线段的长度,以它们为边不能构成三角形的是( )A、3,8,4 B、4,9,6 C、15,20,8 D、9,15,83. 如果等腰三角形的两边长分别为3和6,那么它的周长为( )A、9 B、12 C、15 D、12或154. 如图,点B,E,C,F在同一条直线上,已知 , ,添加下列条件还不能判定的 是( ) A、 B、 C、 D、5. 如图是一个正方形和直角三角形的组合图形,直角三角形的斜边和一条直角边的长分别为10cm,8cm,则该正方形的面积为( )
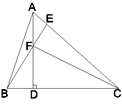
A、 B、 C、 D、5. 如图是一个正方形和直角三角形的组合图形,直角三角形的斜边和一条直角边的长分别为10cm,8cm,则该正方形的面积为( ) A、6cm2 B、36cm2 C、18cm2 D、2cm26. 如图,在 中, , ,点 在 上, , ,则 的长为( )
A、6cm2 B、36cm2 C、18cm2 D、2cm26. 如图,在 中, , ,点 在 上, , ,则 的长为( ) A、 B、 C、 D、7. 如图,在 中, , 平分 , 于E,则下列结论中,不正确的是( )
A、 B、 C、 D、7. 如图,在 中, , 平分 , 于E,则下列结论中,不正确的是( )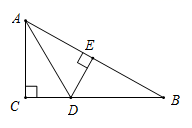 A、 平分 B、 C、 平分 D、8. 如图,在 中, , 为斜边 的中点, 在 内绕点 转动,分别交边 , 于点 , (点 不与点 , 重合),下列说法正确的是( )
A、 平分 B、 C、 平分 D、8. 如图,在 中, , 为斜边 的中点, 在 内绕点 转动,分别交边 , 于点 , (点 不与点 , 重合),下列说法正确的是( )① ;② ;③
 A、①② B、①③ C、②③ D、①②③
A、①② B、①③ C、②③ D、①②③二、填空题
-
9. 已知,如图,在△ABC中,∠C=90°,AD平分∠BAC,CD=2cm,则点D到AB的距离为cm.
 10. 如图, ,其中 , ,则 °.
10. 如图, ,其中 , ,则 °.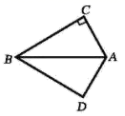 11. 如图,已知 , ,点 、 、 、 在一条直线上,要证 ,还需添加的条件是:.(只需添加一个条件)
11. 如图,已知 , ,点 、 、 、 在一条直线上,要证 ,还需添加的条件是:.(只需添加一个条件)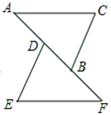 12. 已知等腰三角形的一个内角为 50°,则顶角为.13. 一个三角形的三边分别为7cm,24 cm,25 cm,则此三角形的面积为 cm2.14. 如图,已知正方形A的面积为25,如果正方形C的面积为169,那么正方形B的面积为 .
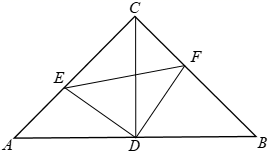
12. 已知等腰三角形的一个内角为 50°,则顶角为.13. 一个三角形的三边分别为7cm,24 cm,25 cm,则此三角形的面积为 cm2.14. 如图,已知正方形A的面积为25,如果正方形C的面积为169,那么正方形B的面积为 . 15. 如图,在 中,DE垂直平分BC交AB于点E , 若 , 的周长为31,则 的周长为 .
15. 如图,在 中,DE垂直平分BC交AB于点E , 若 , 的周长为31,则 的周长为 .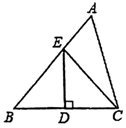 16. 如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,垂足为A,交CD于D,若AD=8,则点P到BC的距离是 .
16. 如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,垂足为A,交CD于D,若AD=8,则点P到BC的距离是 . 17. 如图将矩形 沿直线 折叠,顶点D恰好落在 边上F处,已知 ,则 .
17. 如图将矩形 沿直线 折叠,顶点D恰好落在 边上F处,已知 ,则 .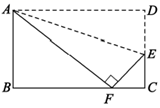 18. 如图,在Rt△ 中, , ,点 在 上,且 ,连接 , ,且 ,连接 ,则 的长为.
18. 如图,在Rt△ 中, , ,点 在 上,且 ,连接 , ,且 ,连接 ,则 的长为.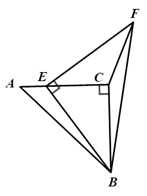
三、解答题
-
19. 已知:如图,点 A、B、C、D 在一条直线上,AC=DB,AE=DF,BE=CF.求证:△ABE≌△DCF.
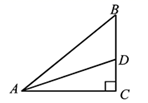
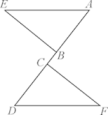 20. 如图∠B=∠ACD=90°, AD=13,CD=12, BC=3,则AB的长是多少?
20. 如图∠B=∠ACD=90°, AD=13,CD=12, BC=3,则AB的长是多少?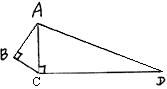 21. 已知:如图,点E在AB上,点C在AD上,AB=AD,∠B=∠D。
21. 已知:如图,点E在AB上,点C在AD上,AB=AD,∠B=∠D。求证:△ABC≌△ADE。
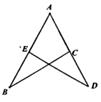 22. 如图所示,PB⊥AB于点B , PC⊥AC于点C , 且PB=PC , D是AP上一点.
22. 如图所示,PB⊥AB于点B , PC⊥AC于点C , 且PB=PC , D是AP上一点.求证:∠BDP=∠CDP.
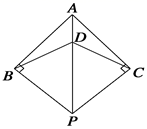 23. 如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE.求证:△ACD≌△CBE.
23. 如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE.求证:△ACD≌△CBE. 24. 已知:如图,△ABC中,∠ACB=45°,AD⊥BC于D,CF交AD于点F,连接BF并延长交AC于点E,∠BAD=∠FCD.求证:△ABD≌△CFD.
24. 已知:如图,△ABC中,∠ACB=45°,AD⊥BC于D,CF交AD于点F,连接BF并延长交AC于点E,∠BAD=∠FCD.求证:△ABD≌△CFD.