北师大版初中数学2021-2022学年九年级上学期期中测试模拟卷(一)
试卷更新日期:2021-10-26 类型:期中考试
一、单选题
-
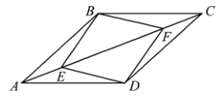
1. 如图,D、E、F分别是 各边中点,则以下说法错误的是( )
 A、 和 的面积相等 B、四边形 是平行四边形 C、若 ,则四边形 是菱形 D、若 ,则四边形 是矩形2. 已知关于x的一元二次方程 有两个不相等的实数根,则a的取值范围是( )A、 B、 C、 且 D、 且3. 如图,在边长为2的正方形ABCD中,若将AB绕点A逆时针旋转 ,使点B落在点 的位置,连接B ,过点D作DE⊥ ,交 的延长线于点E,则 的长为( )
A、 和 的面积相等 B、四边形 是平行四边形 C、若 ,则四边形 是菱形 D、若 ,则四边形 是矩形2. 已知关于x的一元二次方程 有两个不相等的实数根,则a的取值范围是( )A、 B、 C、 且 D、 且3. 如图,在边长为2的正方形ABCD中,若将AB绕点A逆时针旋转 ,使点B落在点 的位置,连接B ,过点D作DE⊥ ,交 的延长线于点E,则 的长为( )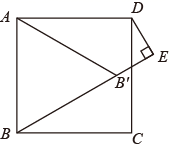 A、 B、 C、 D、4. 已知关于x的一元二次方程x2-kx+k-3=0的两个实数根分别为 ,且 ,则k的值是( )A、-2 B、2 C、-1 D、15. 用配方法解一元二次方程 ,配方正确的是( ).A、 B、 C、 D、6. 如图,在矩形纸片ABCD中, , ,M是BC上的点,且 .将矩形纸片ABCD沿过点M的直线折叠,使点D落在AB上的点P处,点C落在点 处,折痕为MN,则线段PA的长是( )
A、 B、 C、 D、4. 已知关于x的一元二次方程x2-kx+k-3=0的两个实数根分别为 ,且 ,则k的值是( )A、-2 B、2 C、-1 D、15. 用配方法解一元二次方程 ,配方正确的是( ).A、 B、 C、 D、6. 如图,在矩形纸片ABCD中, , ,M是BC上的点,且 .将矩形纸片ABCD沿过点M的直线折叠,使点D落在AB上的点P处,点C落在点 处,折痕为MN,则线段PA的长是( ) A、4 B、5 C、6 D、7. 在解一元二次方程x2+px+q=0时,小红看错了常数项q,得到方程的两个根是﹣3,1.小明看错了一次项系数P,得到方程的两个根是5,﹣4,则原来的方程是( )A、x2+2x﹣3=0 B、x2+2x﹣20=0 C、x2﹣2x﹣20=0 D、x2﹣2x﹣3=08. 如图,在△ABC中,点D、E分别是AB、AC的中点,若△ADE的面积是3cm2 , 则四边形BDEC的面积为( )
A、4 B、5 C、6 D、7. 在解一元二次方程x2+px+q=0时,小红看错了常数项q,得到方程的两个根是﹣3,1.小明看错了一次项系数P,得到方程的两个根是5,﹣4,则原来的方程是( )A、x2+2x﹣3=0 B、x2+2x﹣20=0 C、x2﹣2x﹣20=0 D、x2﹣2x﹣3=08. 如图,在△ABC中,点D、E分别是AB、AC的中点,若△ADE的面积是3cm2 , 则四边形BDEC的面积为( ) A、12cm2 B、9cm2 C、6cm2 D、3cm29. 如图,在菱形 中, 是 的中点, ,交 于点 ,如果 ,那么菱形 的周长是( )
A、12cm2 B、9cm2 C、6cm2 D、3cm29. 如图,在菱形 中, 是 的中点, ,交 于点 ,如果 ,那么菱形 的周长是( )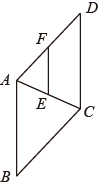 A、11 B、22 C、33 D、4410. 有一个人患了流行性感冒,经过两轮传染后共有144人患了流行性感冒,则每轮传染中平均一个人传染的人数是( )A、14 B、11 C、10 D、911. 如图, 中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作 的位似图形 ,并把 的边长放大到原来的2倍,设点B的横坐标是a , 则点B的对应点 的横坐标是( )
A、11 B、22 C、33 D、4410. 有一个人患了流行性感冒,经过两轮传染后共有144人患了流行性感冒,则每轮传染中平均一个人传染的人数是( )A、14 B、11 C、10 D、911. 如图, 中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作 的位似图形 ,并把 的边长放大到原来的2倍,设点B的横坐标是a , 则点B的对应点 的横坐标是( ) A、 B、 C、 D、12. 如图,在正方形ABCD中,E,F是对角线AC上的两点,且EF=2AE=2CF,连接DE并延长交AB于点M,连接DF并延长交BC于点N,连接MN,则 ( )
A、 B、 C、 D、12. 如图,在正方形ABCD中,E,F是对角线AC上的两点,且EF=2AE=2CF,连接DE并延长交AB于点M,连接DF并延长交BC于点N,连接MN,则 ( ) A、 B、 C、1 D、
A、 B、 C、1 D、二、填空题
-
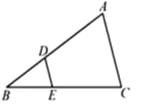
13. 如图,在 中,点 分别在边 上,且 , 与四边形 的面积的比为.
 14. 已知在平面直角坐标系中,△AOB的顶点分别为点A(2,1)、点B(2,0)、点O(0,0),若以原点O为位似中心,相似比为2,将△AOB放大,则点A的对应点的坐标为.15. 如图,在菱形ABCD中, , ,Q为AB的中点,P为对角线BD上的任意一点,则 的最小值为.
14. 已知在平面直角坐标系中,△AOB的顶点分别为点A(2,1)、点B(2,0)、点O(0,0),若以原点O为位似中心,相似比为2,将△AOB放大,则点A的对应点的坐标为.15. 如图,在菱形ABCD中, , ,Q为AB的中点,P为对角线BD上的任意一点,则 的最小值为. 16. 不透明的布袋中有红、黄、蓝3种只是颜色不同的钢笔各1支,先从中摸出1支,记录下它的颜色,将它放回布袋并搅匀,再从中随机摸出1支,记录下颜色,那么这两次摸出的钢笔为红色、黄色各一支的概率为.17. 如图,把边长为3的正方形OABC绕点O逆时针旋转n°(0<n<90)得到正方形ODEF,DE与BC交于点P,ED的延长线交AB于点Q,交OA的延长线于点M.若BQ:AQ=3:1,则AM=.
16. 不透明的布袋中有红、黄、蓝3种只是颜色不同的钢笔各1支,先从中摸出1支,记录下它的颜色,将它放回布袋并搅匀,再从中随机摸出1支,记录下颜色,那么这两次摸出的钢笔为红色、黄色各一支的概率为.17. 如图,把边长为3的正方形OABC绕点O逆时针旋转n°(0<n<90)得到正方形ODEF,DE与BC交于点P,ED的延长线交AB于点Q,交OA的延长线于点M.若BQ:AQ=3:1,则AM=.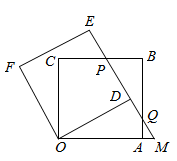 18. 如图,点D,E分别在△ABC的边AC,AB上,△ADE∽△ABC,M,N分别是DE,BC的中点,若 = ,则 =.
18. 如图,点D,E分别在△ABC的边AC,AB上,△ADE∽△ABC,M,N分别是DE,BC的中点,若 = ,则 =.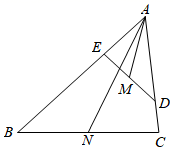
三、解答题
-
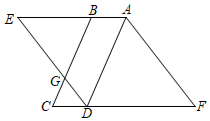
19. 解方程: .20. 解方程:2x2﹣x﹣3=0.21. 如图,在 中,G为BC边上一点, ,延长DG交AB的延长线于点E , 过点A作 交CD的延长线于点F . 求证:四边形AEDF是菱形.
 22. 如图,甲、乙两个转盘均被分成3个面积相等的扇形,每个扇形中都标有相应的数字,同时转动两个转盘(当指针指在边界线上时视为无效,需重新转动转盘),当转盘停止后,把甲、乙两个转盘中指针所指数字分别记为x , y . 请用树状图或列表法求点 落在平面直角坐标系第一象限内的概率.
22. 如图,甲、乙两个转盘均被分成3个面积相等的扇形,每个扇形中都标有相应的数字,同时转动两个转盘(当指针指在边界线上时视为无效,需重新转动转盘),当转盘停止后,把甲、乙两个转盘中指针所指数字分别记为x , y . 请用树状图或列表法求点 落在平面直角坐标系第一象限内的概率. 23. 列方程(组)解应用题
23. 列方程(组)解应用题端午节期间,某水果超市调查某种水果的销售情况,下面是调查员的对话:
小王:该水果的进价是每千克22元;
小李:当销售价为每千克38元时,每天可售出160千克;若每千克降低3元,每天的销售量将增加120千克.
根据他们的对话,解决下面所给问题:超市每天要获得销售利润3640元,又要尽可能让顾客得到实惠,求这种水果的销售价为每千克多少元?
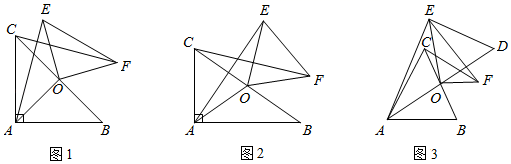
24. 如图,在 和 中, , . (1)、求证: ;(2)、若 , ,求 的长.
(1)、求证: ;(2)、若 , ,求 的长.