北师大版初中数学2021-2022学年八年级上学期期中测试模拟卷(二)
试卷更新日期:2021-10-26 类型:期中考试
一、单选题
-
1. 在平面直角坐标系中,若点P(a-3,1)与点Q(2,b+1)关于x轴对称,则a+b的值是( )A、1 B、2 C、3 D、42. 如图,一个弹簧不挂重物时长6cm,挂上重物后,在弹性限度内弹簧伸长的长度与所挂重物的质量成正比.弹簧总长y(单位:cm)关于所挂物体质量x(单位:kg)的函数图象如图所示,则图中a的值是( )
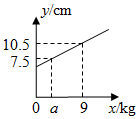 A、3 B、4 C、5 D、63. 下列计算正确的是( )A、 3 B、 C、 D、( )2=24. 如图,在矩形ABCD中,AB=5,AD=3,点E为BC上一点,把△CDE沿DE翻折,点C 恰好落在AB边上的F处,则CE的长是( )
A、3 B、4 C、5 D、63. 下列计算正确的是( )A、 3 B、 C、 D、( )2=24. 如图,在矩形ABCD中,AB=5,AD=3,点E为BC上一点,把△CDE沿DE翻折,点C 恰好落在AB边上的F处,则CE的长是( ) A、1 B、 C、 D、5. 如图,若数轴上两点 , 所对应的实数分别为 , ,则 的值可能是( )
A、1 B、 C、 D、5. 如图,若数轴上两点 , 所对应的实数分别为 , ,则 的值可能是( )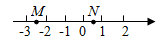 A、2 B、1 C、-1 D、-26. 设 的整数部分为a , 小数部分为b , 则 的值是( )A、6 B、 C、12 D、7. 点 在函数 的图象上,则代数式 的值等于( )A、5 B、-5 C、7 D、-68. 如图,将矩形 折叠,使点C和点A重合,折痕为 , 与 交于点O若 , ,则 的长为( )
A、2 B、1 C、-1 D、-26. 设 的整数部分为a , 小数部分为b , 则 的值是( )A、6 B、 C、12 D、7. 点 在函数 的图象上,则代数式 的值等于( )A、5 B、-5 C、7 D、-68. 如图,将矩形 折叠,使点C和点A重合,折痕为 , 与 交于点O若 , ,则 的长为( )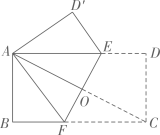 A、 B、 C、 D、9. 已知 .若 为整数且 ,则 的值为( )A、43 B、44 C、45 D、4610. 数形结合是解决数学问题常用的思思方法.如图,直线y=x+5和直线y=ax+b,相交于点P ,根据图象可知,方程x+5=ax+b的解是( )
A、 B、 C、 D、9. 已知 .若 为整数且 ,则 的值为( )A、43 B、44 C、45 D、4610. 数形结合是解决数学问题常用的思思方法.如图,直线y=x+5和直线y=ax+b,相交于点P ,根据图象可知,方程x+5=ax+b的解是( ) A、x=20 B、x=5 C、x=25 D、x=1511. 《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读 ,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙 的距离为 寸,点 和点 距离门槛 都为 尺( 尺 寸),则 的长是( )
A、x=20 B、x=5 C、x=25 D、x=1511. 《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读 ,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙 的距离为 寸,点 和点 距离门槛 都为 尺( 尺 寸),则 的长是( ) A、 寸 B、 寸 C、 寸 D、 寸12. 已知A,B两地相距60km,甲、乙两人沿同一条公路从A地出发到B地,甲骑自行车匀速行驶3h到达,乙骑摩托车.比甲迟1h出发,行至30km处追上甲,停留半小时后继续以原速行驶.他们离开A地的路程y与甲行驶时间x的函数图象如图所示.当乙再次追上甲时距离B地( )
A、 寸 B、 寸 C、 寸 D、 寸12. 已知A,B两地相距60km,甲、乙两人沿同一条公路从A地出发到B地,甲骑自行车匀速行驶3h到达,乙骑摩托车.比甲迟1h出发,行至30km处追上甲,停留半小时后继续以原速行驶.他们离开A地的路程y与甲行驶时间x的函数图象如图所示.当乙再次追上甲时距离B地( )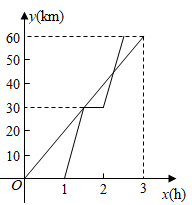 A、15km B、16km C、44km D、45km
A、15km B、16km C、44km D、45km二、填空题
-
13. 甲、乙、丙三名同学观察完某个一次函数的图象,各叙述如下:
甲:函数的图象经过点(0,1);
乙:y随x的增大而减小;
丙:函数的图象不经过第三象限.
根据他们的叙述,写出满足上述性质的一个函数表达式为 .
14. 如图,在△ABC中,AC=4,∠A=60°,∠B=45°,BC边的垂直平分线DE交AB于点D , 连接CD , 则AB的长为 .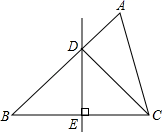 15. 如图,某港口P位于东西方向的海岸线上,甲、乙轮船同时离开港口,各自沿一固定方向航行,甲、乙轮船每小时分别航行12海里和16海里,1小时后两船分别位于点A,B处,且相距20海里,如果知道甲船沿北偏西 方向航行,则乙船沿方向航行.
15. 如图,某港口P位于东西方向的海岸线上,甲、乙轮船同时离开港口,各自沿一固定方向航行,甲、乙轮船每小时分别航行12海里和16海里,1小时后两船分别位于点A,B处,且相距20海里,如果知道甲船沿北偏西 方向航行,则乙船沿方向航行.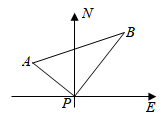 16. 如图,点 与点 关于直线 对称,则 .
16. 如图,点 与点 关于直线 对称,则 . 17. 育红学校七年级学生步行到郊外旅行.七(1)班出发1h后,七(2)班才出发,同时七(2)班派一名联络员骑自行车在两班队伍之间进行联络,联络员和七(1)班的距离s(km)与七(2)班行进时间t(h)的函数关系图象如图所示.若已知联络员用了 第一次返回到自己班级,则七(2)班需要 h才能追上七(1)班.
17. 育红学校七年级学生步行到郊外旅行.七(1)班出发1h后,七(2)班才出发,同时七(2)班派一名联络员骑自行车在两班队伍之间进行联络,联络员和七(1)班的距离s(km)与七(2)班行进时间t(h)的函数关系图象如图所示.若已知联络员用了 第一次返回到自己班级,则七(2)班需要 h才能追上七(1)班.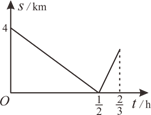 18. 2021年5月7日,《科学》杂志发布了我国成功研制出可编程超导量子计算机“祖冲之”号的相关研究成果.祖冲之是我国南北朝时期杰出的数学家,他是第一个将圆周率 精确到小数点后第七位的人,他给出 的两个分数形式: (约率)和 (密率).同时期数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法,其理论依据是:设实数 的不足近似值和过剩近似值分别为 和 (即有 ,其中 , , , 为正整数),则 是 的更为精确的近似值.例如:已知 ,则利用一次“调日法”后可得到 的一个更为精确的近似分数为: ;由于 ,再由 ,可以再次使用“调日法”得到 的更为精确的近似分数……现已知 ,则使用两次“调日法”可得到 的近似分数为.
18. 2021年5月7日,《科学》杂志发布了我国成功研制出可编程超导量子计算机“祖冲之”号的相关研究成果.祖冲之是我国南北朝时期杰出的数学家,他是第一个将圆周率 精确到小数点后第七位的人,他给出 的两个分数形式: (约率)和 (密率).同时期数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法,其理论依据是:设实数 的不足近似值和过剩近似值分别为 和 (即有 ,其中 , , , 为正整数),则 是 的更为精确的近似值.例如:已知 ,则利用一次“调日法”后可得到 的一个更为精确的近似分数为: ;由于 ,再由 ,可以再次使用“调日法”得到 的更为精确的近似分数……现已知 ,则使用两次“调日法”可得到 的近似分数为.三、解答题
-
19. 计算:(1)、(2)、20. 计算(1)、(2)、21. 阅读理解:
∵ ,即2< <3,∴1< -1<2,
∴ -1的整数部分为1,
∴ -1的小数部分为 -2
解决问题:
已知a是 -3的整数部分,b是 -3的小数部分,求(-a)3+(b+4)2的平方根
22. 如图,一架梯子 斜靠在一竖直的墙 上,这时 , .梯子顶端 沿墙下滑至点 ,使 ,同时,梯子底端 也外移至点 .求 的长度.(结果保留根号)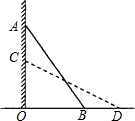 23. 如图,平面直角坐标系中,△ABC的顶点坐标分别为A(4,1),B(3,4),C(1,2).
23. 如图,平面直角坐标系中,△ABC的顶点坐标分别为A(4,1),B(3,4),C(1,2).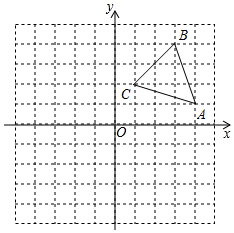 (1)、画出△ABC关于y轴对称的△A1B1C1 , 并写出顶点C1的坐标;(2)、若点P在x轴上,且满足PA+PC1最小,求点P的坐标及PA+PC1的最小值.24. 如图1,小刚家,学校、图书馆在同一条直线上,小刚骑自行车匀速从学校到图书馆,到达图书馆还完书后,再以相同的速度原路返回家中(上、下车时间忽略不计).小刚离家的距离 与他所用的时间 的函数关系如图2所示.
(1)、画出△ABC关于y轴对称的△A1B1C1 , 并写出顶点C1的坐标;(2)、若点P在x轴上,且满足PA+PC1最小,求点P的坐标及PA+PC1的最小值.24. 如图1,小刚家,学校、图书馆在同一条直线上,小刚骑自行车匀速从学校到图书馆,到达图书馆还完书后,再以相同的速度原路返回家中(上、下车时间忽略不计).小刚离家的距离 与他所用的时间 的函数关系如图2所示. (1)、小刚家与学校的距离为 ,小刚骑自行车的速度为 ;(2)、求小刚从图书馆返回家的过程中, 与 的函数表达式;(3)、小刚出发35分钟时,他离家有多远?25. 小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1 , y1),P2(x2 , y2),可通过构造直角三角形利用图1得到结论:P1P2= 他还利用图2证明了线段P1P2的中点P(x,y)P的坐标公式:x= ,y= .
(1)、小刚家与学校的距离为 ,小刚骑自行车的速度为 ;(2)、求小刚从图书馆返回家的过程中, 与 的函数表达式;(3)、小刚出发35分钟时,他离家有多远?25. 小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1 , y1),P2(x2 , y2),可通过构造直角三角形利用图1得到结论:P1P2= 他还利用图2证明了线段P1P2的中点P(x,y)P的坐标公式:x= ,y= . (1)、请你帮小明写出中点坐标公式的证明过程;(2)、①已知点M(2,﹣1),N(﹣3,5),则线段MN长度为;
(1)、请你帮小明写出中点坐标公式的证明过程;(2)、①已知点M(2,﹣1),N(﹣3,5),则线段MN长度为;②直接写出以点A(2,2),B(﹣2,0),C(3,﹣1),D为顶点的平行四边形顶点D的坐标:;
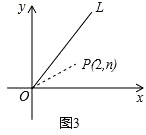
(3)、如图3,点P(2,n)在函数y= x(x≥0)的图象OL与x轴正半轴夹角的平分线上,请在OL、x轴上分别找出点E、F,使△PEF的周长最小,简要叙述作图方法,并求出周长的最小值.