苏科版初中数学2021-2022学年七年级上学期期中测试模拟卷
试卷更新日期:2021-10-26 类型:期中考试
一、单选题
-
1. 有理数 的相反数是( )A、 B、 C、3 D、-32. 下列运算正确的是( )A、 B、 C、 D、3. 代数式a+b2的意义是( )
A、a与b的和的平方 B、a与b两数的平方和 C、a与b的平方的和 D、a与b的平方4. 在体育课的立定跳远测试中,以2.00m为标准,若小明跳出了2.35m,可记作+0.35m,则小亮跳出了1.75m,应记作( )A、+0.25m B、-0.25m C、+0.35m D、-0.35m5. 在﹣(﹣2)、﹣|﹣2|、 、 中正数有( )A、1个 B、2个 C、3个 D、4个6. 在有理数1,0, ,-2中,任意取两个数相加,最小的和是( )A、 B、 C、 D、7. 一根1米长的绳子,第一次剪去它的三分之一,如此剪下去,第五次后剩下的绳子的长度为( )A、 米 B、 米 C、 米 D、 米8. 已知a,b是有理数, , ,若将a,b在数轴上表示,则图中有可能( )A、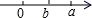 B、
B、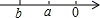 C、
C、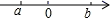 D、
D、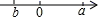
二、填空题
-
9. ﹣3的倒数为 .10. 据国家旅游局统计,2021年端午小长假全国各大景点共接待游客约为8260000人次,数据8260000用科学记数法表示为。11. 比较大小:12. 单项式 的系数是;次数是.13. 下列各数3.1415926,3,1.212222……, ,2-π,-2020中,无理数的个数有个.14. 单项式 与 是同类项,则 .15. 已知x+2y=2,则1-2x-4y的值等于.16. 厂家检测甲、乙、丙、丁四个足球的质量,超过标准质量的克数记为正数,不足标准质量的克数记为负数,结果如图所示,其中最接近标准质量的足球是 .
 17. 按下列程序进行运算(如图),若输入13,则输出的值为.
17. 按下列程序进行运算(如图),若输入13,则输出的值为. 18. 填在下面各正方形中的四个数之间都有一定的规律,按此规律得出a+b+c= .
18. 填在下面各正方形中的四个数之间都有一定的规律,按此规律得出a+b+c= .
三、解答题
-
19. 计算(1)、(2)、(3)、(4)、20. 化简
(1)、﹣3x2y+2x2y+3xy2﹣xy2(2)、4x2﹣(2x2+x﹣1)+(2﹣x2+3x)21. 先化简,再求值: ,其中22. 某检测小组乘汽车检修供电线路,约定向东方向出发为正,向西方向出发为负,某天检测小组自A地出发到收工时,行驶情况(单位:km)为:+22,-3,+4,-2,-8,+17,-2,-3,+12,+7,-5 .
(1)收工时车辆停在何处?
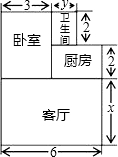
(2)若每千米耗油0.2升,从A地出发到收工共耗油多少升?23. 规定一种新的运算:a★b=a×b-a-b2+1,例如3★(-4)=3×(-4)-3-(-4)2+1,请用上述规定计算下面各式:(1)、1★5;(2)、(-5) ★ [ 3★(-1)]24. 王老师购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位:m),解答下列问题:①写出用含x、y的整式表示的地面总面积;
②若x=4m , y=1.5m , 铺1m2地砖的平均费用为80元,求铺地砖的总费用为多少元?
 25. 王叔叔家的装修工程接近尾声,油漆工程结束了,经统计,油漆工共做50工时,用了150L油漆,已知油漆每升128元,共粉刷120m2 , 在结算工钱时,有以下几种结算方案:
25. 王叔叔家的装修工程接近尾声,油漆工程结束了,经统计,油漆工共做50工时,用了150L油漆,已知油漆每升128元,共粉刷120m2 , 在结算工钱时,有以下几种结算方案:( 1 )按工时算,每6工时为300元;
( 2 )按油漆费用来算,油漆费用的15%为工钱;
( 3 )按粉刷面积来算,每6m2为132元.
请你帮王叔叔算一下,用哪种方案最省钱?
26. 我们知道简便计算的好处,事实上,简便计算在好多地方都存在,观察下列等式:152=1×2×100+25=225,252=2×3×100+25=625,352=3×4×100+25=1225,…
(1)根据上述格式反应出的规律计算:952 ;
(2)设这类等式左边两位数的十位数字为a,请用一个含a的代数式表示其结果;
(3)这种简便计算也可以推广应用:个位数字是5的三位数的平方,请写出1952的简便计算过程及结果.