山东省菏泽市牡丹区2021-2022学年八年级上学期数学第一次月考试卷

试卷更新日期：2021-10-26 类型：月考试卷

进入出卷网下载

一、单选题

1. 在实数 $\frac{1}{3}$ ， $\sqrt{10}$ ， $- \sqrt{\frac{4}{25}}$ ， $π$ ， $\sqrt[3]{- 8}$ 中无理数有（）．

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列二次根式能与 $\sqrt{3}$ 合并的是（）．

A、 $\sqrt{12}$ B、 $\sqrt{10}$ C、 $\sqrt{8}$ D、 $\sqrt{6}$

查看试题解析
3. 三个正方形的面积如图所示，则面积为 $A$ 的正方形的边长为（）

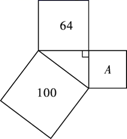A、164 B、36 C、8 D、6

查看试题解析
4. 下列说法正确的是（）．

A、实数分为正实数和负实数 B、无理数与数轴上的点一一对应 C、-2是4的平方根 D、两个无理数的和一定是无理数

查看试题解析
5. 若 $a = \sqrt{3}$ ， $b = | - 6 |$ ， $c = \sqrt[3]{65}$ ，则下列关系正确的是（）．

A、 $a > b > c$ B、 $c > b > a$ C、 $b > a > c$ D、 $b > c > a$

查看试题解析
6. 下列各组线段中的三个长度：①9，12，15；②7，24，25；③3² ， 4² ， 5²；④3a，4a，5a（a＞0）；⑤m²﹣n² ， 2mn，m²+n²（m，n为正整数，且m＞n）其中可以构成直角三角形的有（）

A、5组 B、4组 C、3组 D、2组

查看试题解析
7. 如图，小华将升旗的绳子拉紧到旗杆底端点B，绳子末端刚好接触到地面，然后拉紧绳子使其末端到点D处，点D到地面的距离CD长为2m，点D到旗杆AB的水平距离为8m，若设旗杆的高度AB长为xm，则根据题意所列的方程是（）．

A、 ${(x - 2)}^{2} + 8^{2} = x^{2}$ B、 ${(x + 2)}^{2} + 8^{2} = x^{2}$ C、 $x^{2} + 8^{2} = {(x - 2)}^{2}$ D、 $x^{2} + 8^{2} = {(x + 2)}^{2}$

查看试题解析
8. 在 $△ A B C$ 中， $A B = 25$ ， $A C = 17$ ，BC上的高AD长为15，则 $△ A B C$ 的面积为（）．

A、210 B、90 C、210或90 D、84或120

查看试题解析
9. 已知 $\sqrt[3]{2 x + 1} = 2 x + 1$ ，则x的值为（）．

A、0 B、 $- 1$ C、 $- \frac{1}{2}$ D、0， $- 1$ 或 $- \frac{1}{2}$

查看试题解析
10. 如图是一个供滑板爱好者使用的U型池，该U型池可以看作是一个长方体去掉一个“半圆柱”而成，中间可供滑行的部分的截面是半径为 $2.5 m$ 的半圆，其边缘 $A B = C D = 20 m$ ．小明要在AB上选取一点E，能够使他从点D滑到点E再滑到点C的滑行距离最短，则他滑行的最短距离约为（）m．（ $π$ 取3）

A、30 B、28 C、25 D、22

查看试题解析

二、填空题

11. $\sqrt{81}$ 的平方根是．

查看试题解析
12. 已知一个正数x的两个平方根分别是 $3 a - 6$ 和 $- a - 4$ ，则这个正数x的值是．

查看试题解析
13. 如图，数轴上点A表示的实数是.

查看试题解析
14. 已知 $x = \sqrt{5} + 1$ ，则 $x^{2} - 2 x + 3 =$ ．

查看试题解析
15. 已知两条线段的长为5cm和12cm，当第三条线段的长为cm时，这三条线段能组成一个直角三角形．

查看试题解析
16. 若 $\sqrt{a - 2} + | b + 3 | = 0$ ，则 $a - b$ 的算术平方根是．

查看试题解析
17. 如图，在正方形网格中，若每个小方格的边长都为1，则 $△ A B C$ 的面积为．

查看试题解析
18. 课间，小明拿着老师的等腰直角三角板玩，不小心掉到两墙之间（如图）， $∠ A C B = 90 °$ ， $A C = B C$ ，从三角板的刻度可知 $A B = 26 cm$ ，小明很快就知道了砌墙砖块的厚度为 cm（每块砖的厚度相等）．

查看试题解析

三、解答题

19. 计算：
① $| \sqrt{3} - 2 | + {(\frac{1}{2})}^{- 1} - {(π - 3.14)}^{0} - \sqrt[3]{27}$

② $\sqrt{\frac{4}{3}} \div \sqrt{\frac{3}{2}} \times \sqrt{1 \frac{1}{8}}$

③ $\sqrt{3} + {(- 2 \sqrt{3})}^{2} - (\sqrt{48} - \sqrt{\frac{1}{2}} \times \sqrt{6})$

④ $(2 \sqrt{3} + 3) (2 \sqrt{3} - 3) - {(\sqrt{3} - 1)}^{2}$

查看试题解析
20. 求满足下列各式的未知数x的值．

(1)、 $3 {(x - 1)}^{2} = 27$

(2)、 $\frac{1}{2} {(x + 6)}^{3} = - 32$

查看试题解析
21. 已知 $2 a - 1$ 的算术平方根是3， $a - b + 2$ 的立方根是2，求 $a - 4 b$ 的平方根．

查看试题解析
22. 如图，在 $Rt △ A B C$ 中， $∠ C = 90 °$ ， $A B = 13$ ， $A C = 5$ ，AD平分 $∠ C A B$ 交CB于点D，求CD的长．

查看试题解析
23. 阅读下列材料，然后回答问题，在进行二次根式的化简与运算时，我们有时会碰上如 $\frac{2}{\sqrt{3} + 1}$ 一样的式子，其实我们还可以将其进一步化简：
$\frac{2}{\sqrt{3} + 1} = \frac{2 \times (\sqrt{3} - 1)}{(\sqrt{3} + 1) (\sqrt{3} - 1)} = \frac{2 (\sqrt{3} - 1)}{{(\sqrt{3})}^{2} - 1^{2}} = \sqrt{3} - 1$ ①

以上这种化简的步骤叫做分母有理化．

$\frac{2}{\sqrt{3} + 1}$ 还可以用以下方法化简：

$\frac{2}{\sqrt{3} + 1} = \frac{3 - 1}{\sqrt{3} + 1} = \frac{{(\sqrt{3})}^{2} - 1^{2}}{\sqrt{3} + 1} = \frac{(\sqrt{3} + 1) (\sqrt{3} - 1)}{\sqrt{3} + 1} = \sqrt{3} - 1$ ②

(1)、请参照①②的方法用两种方法化简： $\frac{2}{\sqrt{7} + \sqrt{5}}$

(2)、直接写出化简结果： $\frac{2}{\sqrt{13} + \sqrt{11}} =$ ； $\frac{2}{\sqrt{15} + \sqrt{13}} =$ ．

(3)、计算： $\frac{3}{\sqrt{5} + \sqrt{2}} + \frac{3}{\sqrt{8} + \sqrt{5}} + \frac{3}{\sqrt{11} + \sqrt{8}} + \dots + \frac{3}{\sqrt{32} + \sqrt{29}} + \frac{3}{\sqrt{35} + \sqrt{32}}$

查看试题解析