山东省滨州市集团校联考2021-2022学年八年级上学期数学第一次月考试卷
试卷更新日期:2021-10-26 类型:月考试卷
一、单选题
-
1. 下列交通标志是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,已知 平分 ,那么就可以证明 ,理由是( )
2. 如图,已知 平分 ,那么就可以证明 ,理由是( ) A、 B、 C、 D、3. 如图, 中, ,D、E分别是 两点,且 ,连接 .则 的度数为( )度·
A、 B、 C、 D、3. 如图, 中, ,D、E分别是 两点,且 ,连接 .则 的度数为( )度· A、45 B、52.5 C、67.5 D、754. 如图,在 中, , ,BD是 的平分线,设 、 的面积分别为 、 ,则 ( )
A、45 B、52.5 C、67.5 D、754. 如图,在 中, , ,BD是 的平分线,设 、 的面积分别为 、 ,则 ( ) A、 B、 C、 D、5. 如图,小明书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )
A、 B、 C、 D、5. 如图,小明书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( ) A、 B、 C、 D、6. 如图,在 中, ,利用尺规在 , 上分别截取 , ,使 ;分别以D,E为圆心、以大于 的长为半径作弧,两弧在 内交于点F;作射线 交 于点H.若 ,P为 上一动点,则 的最小值是( )
A、 B、 C、 D、6. 如图,在 中, ,利用尺规在 , 上分别截取 , ,使 ;分别以D,E为圆心、以大于 的长为半径作弧,两弧在 内交于点F;作射线 交 于点H.若 ,P为 上一动点,则 的最小值是( ) A、 B、2 C、1 D、无法确定7. 如图,在等边三角形 中, , 分别是 , 的中点,点 是线段 上的一个动点,当 的周长最小时, 点的位置在( )
A、 B、2 C、1 D、无法确定7. 如图,在等边三角形 中, , 分别是 , 的中点,点 是线段 上的一个动点,当 的周长最小时, 点的位置在( ) A、 点处 B、 点处 C、 的中点处 D、 三条高的交点处8. 点P(−3,5)关于 轴的对称点的坐标为( )A、 B、 C、 D、9. 如图, 是 的边 上的中线, ,则 的取值范围为( )
A、 点处 B、 点处 C、 的中点处 D、 三条高的交点处8. 点P(−3,5)关于 轴的对称点的坐标为( )A、 B、 C、 D、9. 如图, 是 的边 上的中线, ,则 的取值范围为( ) A、 B、 C、 D、10. 等腰三角形一腰上的高与另一腰的夹角为 ,则顶角的度数为( )A、 B、 C、 D、 或11. 如图,点O为直线AB上一点,射线OC,OD,OE都在直线AB的上方,∠COD=90°,下列说法:①若OD平分∠BOE,则∠AOC的余角和∠AOD的补角都有两个;②若OC平分∠AOE,则有OD平分∠BOE;③若OE平分∠BOC,则OC平分∠AOE;④若OE平分∠BOC,则有∠AOC=2∠DOE,其中结论正确的个数有( )
A、 B、 C、 D、10. 等腰三角形一腰上的高与另一腰的夹角为 ,则顶角的度数为( )A、 B、 C、 D、 或11. 如图,点O为直线AB上一点,射线OC,OD,OE都在直线AB的上方,∠COD=90°,下列说法:①若OD平分∠BOE,则∠AOC的余角和∠AOD的补角都有两个;②若OC平分∠AOE,则有OD平分∠BOE;③若OE平分∠BOC,则OC平分∠AOE;④若OE平分∠BOC,则有∠AOC=2∠DOE,其中结论正确的个数有( ) A、1个 B、2个 C、3个 D、4个12. 如图,已知 , , , , 和 交于 点,则下列结论:① ;② ;③ 平分 ;④ .其中正确的有( )
A、1个 B、2个 C、3个 D、4个12. 如图,已知 , , , , 和 交于 点,则下列结论:① ;② ;③ 平分 ;④ .其中正确的有( ) A、①② B、①②③ C、①②③④ D、①②④
A、①② B、①②③ C、①②③④ D、①②④二、填空题
-
13. 含 角的直角三角形性质:在直角三角形中,如果一个锐角等于 ,那么它所对的等于的一半.14. 如图,已知 ,经分析 , 依据是 .
 15. 如图,在 中, , ,AD是 的一条角平分线,若 ,则 的面积为 .
15. 如图,在 中, , ,AD是 的一条角平分线,若 ,则 的面积为 . 16. 如图,∠1+∠2+∠3+∠4=度.
16. 如图,∠1+∠2+∠3+∠4=度. 17. 如图, 中 平分 ,若 ,则 .
17. 如图, 中 平分 ,若 ,则 . 18. 如图,在 中, 的中垂线交于点P,若 ,则 的度数为 .
18. 如图,在 中, 的中垂线交于点P,若 ,则 的度数为 .
三、解答题
-
19. 已知:如图, ,求线段 的长.
 20. 四边形 在平面直角坐标系中的位置如图所示,每个格子都是长度为1的正方形, 、 、 、 四点在格点上.
20. 四边形 在平面直角坐标系中的位置如图所示,每个格子都是长度为1的正方形, 、 、 、 四点在格点上. (1)、作出四边形 关于 轴对称的四边形 ,并写出点 的坐标;(2)、求四边形 的面积.21. 如图,点P为 和 的平分线的交点.求证:点P在 的平分线上.
(1)、作出四边形 关于 轴对称的四边形 ,并写出点 的坐标;(2)、求四边形 的面积.21. 如图,点P为 和 的平分线的交点.求证:点P在 的平分线上. 22. 如图,在 中, , ,求 的度数.
22. 如图,在 中, , ,求 的度数. 23. 如图,点E在CD上,BC与AE交于点F,AB=CB,BE=BD,∠1=∠2.
23. 如图,点E在CD上,BC与AE交于点F,AB=CB,BE=BD,∠1=∠2.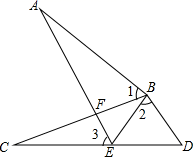 (1)、求证:AE=CD;(2)、证明:∠1=∠3.24. 如图,在等边 中, 厘米, 厘米,如果点 以 厘米/秒的速度运动.
(1)、求证:AE=CD;(2)、证明:∠1=∠3.24. 如图,在等边 中, 厘米, 厘米,如果点 以 厘米/秒的速度运动. (1)、如果点 线段 上由点 向点 运动,点 在线段 上由 点向 点运动. 它们同时出发,若点 的运动速度与点 的运动速度相等. 经过 秒后, 和 是否全等?请说明理由;(2)、在(1)的条件下,当两点的运动时间为多少时, 是一个直角三角形?(3)、若点 的运动速度与点 的运动速度不相等,点 从点 出发,点 以原来的运动速度从点 同时出发,都顺时针沿 三边运动,经过 秒点 与点 第一次相遇,则点 的运动速度是多少厘米/秒.
(1)、如果点 线段 上由点 向点 运动,点 在线段 上由 点向 点运动. 它们同时出发,若点 的运动速度与点 的运动速度相等. 经过 秒后, 和 是否全等?请说明理由;(2)、在(1)的条件下,当两点的运动时间为多少时, 是一个直角三角形?(3)、若点 的运动速度与点 的运动速度不相等,点 从点 出发,点 以原来的运动速度从点 同时出发,都顺时针沿 三边运动,经过 秒点 与点 第一次相遇,则点 的运动速度是多少厘米/秒.