辽宁省鞍山市台安县2021-2022学年八年级上学期数学第一次月考试卷
试卷更新日期:2021-10-26 类型:月考试卷
一、单选题
-
1. 下列长度的三条线段,能组成三角形的是( )A、1,3,4 B、5,6,12 C、5,7,2 D、6,8,102. 如图所示,△ABC 中 AB 边上的高线是( )
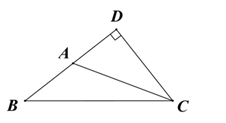 A、线段 DA B、线段 CA C、线段 CD D、线段 BD3. 若等腰三角形的两边长为2和5,则该等腰三角形的周长为( )A、9 B、12 C、9或12 D、74. 将一副三角尺按如图所示的方式摆放,则 的大小为( )
A、线段 DA B、线段 CA C、线段 CD D、线段 BD3. 若等腰三角形的两边长为2和5,则该等腰三角形的周长为( )A、9 B、12 C、9或12 D、74. 将一副三角尺按如图所示的方式摆放,则 的大小为( ) A、 B、 C、 D、5. 只用一种正六边形地砖密铺地板,则能围绕在正六边形的一个顶点处的正六边形地砖有( )A、3块 B、4块 C、5块 D、6块6. 如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A、 B、 C、 D、5. 只用一种正六边形地砖密铺地板,则能围绕在正六边形的一个顶点处的正六边形地砖有( )A、3块 B、4块 C、5块 D、6块6. 如图,若△ABC≌△ADE,则下列结论中一定成立的是( )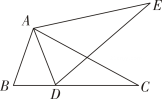 A、AC=DE B、∠BAD=∠CAE C、AB=AE D、∠ABC=∠AED7. 如图, , , ,则能直接判断 的理由是( )
A、AC=DE B、∠BAD=∠CAE C、AB=AE D、∠ABC=∠AED7. 如图, , , ,则能直接判断 的理由是( )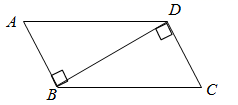 A、 B、 C、 D、8. 如图,在 和 中, ,连接 交于点 ,连接 .下列结论:① ;② ;③ 平分 ;④ 平分 .其中正确的个数为( ).
A、 B、 C、 D、8. 如图,在 和 中, ,连接 交于点 ,连接 .下列结论:① ;② ;③ 平分 ;④ 平分 .其中正确的个数为( ). A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
9. 已知一个 边线的内角和是 ,则 .10. 如图所示,在 中, , , ,则 的度数是 .
 11. 如图, ,则 的度数为;
11. 如图, ,则 的度数为; 12. 若一个三角形三条高的交点在这个三角形的顶点上,则这个三角形是三角形.(填“锐角”“直角”或“钝角”)13. 如图,BC∥EF,AC∥DF,若使△ABC≌△DEF,则需添加一个条件是 .
12. 若一个三角形三条高的交点在这个三角形的顶点上,则这个三角形是三角形.(填“锐角”“直角”或“钝角”)13. 如图,BC∥EF,AC∥DF,若使△ABC≌△DEF,则需添加一个条件是 . 14. 如图,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF= .
14. 如图,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF= .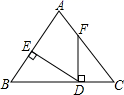 15. 如图,△ABC的面积为16cm2 , BP平分∠ABC,且AP⊥BP于P,则△PBC的面积为 cm2 .
15. 如图,△ABC的面积为16cm2 , BP平分∠ABC,且AP⊥BP于P,则△PBC的面积为 cm2 . 16. 如图,AB=4cm,AC=BD=3cm,∠CAB=∠DBA,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.设运动时间为t(s),则当△ACP与△BPQ全等时,点Q的运动速度为cm/s.
16. 如图,AB=4cm,AC=BD=3cm,∠CAB=∠DBA,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.设运动时间为t(s),则当△ACP与△BPQ全等时,点Q的运动速度为cm/s.
三、解答题
-
17. 一个多边形的每一个内角都相等,并且每个外角都等于和它相邻的内角的一半.(1)、求这个多边形是几边形;
(2)、求这个多边形的内角和
18. 如图,在△ABC中,AD是BC边上的中线,△ABD的周长比△ADC的周长多2,且AB与AC的和为10.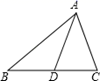 (1)、求AB、AC的长;(2)、求BC边的取值范围.19. 如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.根据下列条件,利用网格点和三角尺画图:
(1)、求AB、AC的长;(2)、求BC边的取值范围.19. 如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.根据下列条件,利用网格点和三角尺画图:
①补全△A′B′C′
②画出AC边上的中线BD;
③画出AC边上的高线BE;
④求△ABD的面积.
20. 如图, .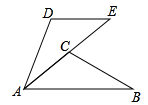 (1)、求 的度数;(2)、若 ,求证: .21. 如图,在 中,E为边CD上一点,F为AD的中点,过点A作 ,交EF的延长线于点B.
(1)、求 的度数;(2)、若 ,求证: .21. 如图,在 中,E为边CD上一点,F为AD的中点,过点A作 ,交EF的延长线于点B.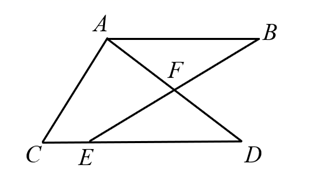 (1)、求证 ;(2)、若 , ,求CD的长.22. 如图,已知 ,点A,B分别在射线OM,ON上移动(不与占O重合),AC平分 ,AC的反向延长线与 的平分线相交于点D.
(1)、求证 ;(2)、若 , ,求CD的长.22. 如图,已知 ,点A,B分别在射线OM,ON上移动(不与占O重合),AC平分 ,AC的反向延长线与 的平分线相交于点D. (1)、当 时, 的度数是多少?(2)、随着点A,B的移动,试问 的度数是否变化?请说出你的理由.23. 如图,四边形 中, , , ,M、N分别为AB、AD上的动点,且 .求证: .
(1)、当 时, 的度数是多少?(2)、随着点A,B的移动,试问 的度数是否变化?请说出你的理由.23. 如图,四边形 中, , , ,M、N分别为AB、AD上的动点,且 .求证: .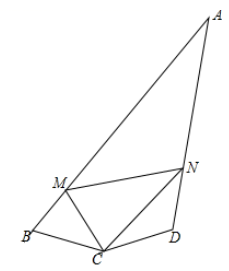 24. 如图①,∠1、∠2是四边形ABCD的两个不相邻的外角.
24. 如图①,∠1、∠2是四边形ABCD的两个不相邻的外角. (1)、猜想并说明∠1+∠2与∠A、∠C的数量关系;(2)、如图②,在四边形ABCD中,∠ABC与∠ADC的平分线交于点O .若∠A=50°,∠C=150°,求∠BOD的度数;(3)、如图③,BO、DO分别是四边形ABCD外角∠CBE、∠CDF的角平分线.请直接写出∠A、∠C与∠O的的数量关系 .25. 如图
(1)、猜想并说明∠1+∠2与∠A、∠C的数量关系;(2)、如图②,在四边形ABCD中,∠ABC与∠ADC的平分线交于点O .若∠A=50°,∠C=150°,求∠BOD的度数;(3)、如图③,BO、DO分别是四边形ABCD外角∠CBE、∠CDF的角平分线.请直接写出∠A、∠C与∠O的的数量关系 .25. 如图 (1)、如图所示,BD,CE是 的高,点P在BD的延长线上, ,点Q在CE上, ,探究PA与AQ之间的关系;(2)、若把(1)中的 改为钝角三角形, , 是钝角,其他条件不变,上述结论是否成立?画出图形并证明你的结论.
(1)、如图所示,BD,CE是 的高,点P在BD的延长线上, ,点Q在CE上, ,探究PA与AQ之间的关系;(2)、若把(1)中的 改为钝角三角形, , 是钝角,其他条件不变,上述结论是否成立?画出图形并证明你的结论.