广东省惠州市惠城区2021-2022学年八年级上学期数学10月月考试卷
试卷更新日期:2021-10-26 类型:月考试卷
一、单选题
-
1. 下面图标中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )A、3cm,4cm,8cm B、8cm,7cm,15cm C、13cm,12cm,20cm D、5cm,5cm,11cm3. 如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )
2. 下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )A、3cm,4cm,8cm B、8cm,7cm,15cm C、13cm,12cm,20cm D、5cm,5cm,11cm3. 如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )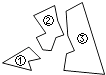 A、带①去 B、带②去 C、带③去 D、带①和②去4. 如图,在 中, , .若 是 的高,与角平分线 相交于点 ,则 的度数为( )
A、带①去 B、带②去 C、带③去 D、带①和②去4. 如图,在 中, , .若 是 的高,与角平分线 相交于点 ,则 的度数为( )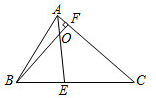 A、130° B、70° C、110° D、100°5. 如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于( )
A、130° B、70° C、110° D、100°5. 如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于( )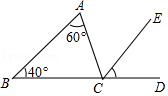 A、40° B、45° C、50° D、55°6. 下列四个图形中,线段BE是△ABC的高的是( )A、
A、40° B、45° C、50° D、55°6. 下列四个图形中,线段BE是△ABC的高的是( )A、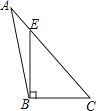 B、
B、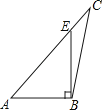 C、
C、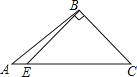 D、
D、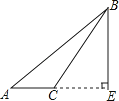 7. 下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )
7. 下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )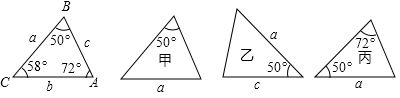 A、甲和乙 B、乙和丙 C、甲和丙 D、只有丙8. 一个多边形的每个内角都等于135°,则这个多边形的边数为( )A、5 B、6 C、7 D、89. 等腰三角形的两边长分别为 , ,则该三角形的周长为( )A、 B、 C、 或 D、以上都不对10. 如图,△ABC的三边AB,BC,CA的长分别为8,12,10,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△AOC等于( )
A、甲和乙 B、乙和丙 C、甲和丙 D、只有丙8. 一个多边形的每个内角都等于135°,则这个多边形的边数为( )A、5 B、6 C、7 D、89. 等腰三角形的两边长分别为 , ,则该三角形的周长为( )A、 B、 C、 或 D、以上都不对10. 如图,△ABC的三边AB,BC,CA的长分别为8,12,10,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△AOC等于( )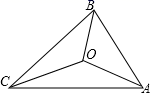 A、1:1:1 B、2:4:3 C、4:6:5 D、4:6:10
A、1:1:1 B、2:4:3 C、4:6:5 D、4:6:10二、填空题
-
11. 如图,自行车的车架做成三角形的形状,该设计是利用三角形的.
 12. 如图,已知在 中, 分别为边 的中点,且 ,则 等于 .
12. 如图,已知在 中, 分别为边 的中点,且 ,则 等于 .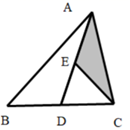 13. 如图,已知AB=AD,要使△ABC≌△ADC,那么应添加的一个条件是 .
13. 如图,已知AB=AD,要使△ABC≌△ADC,那么应添加的一个条件是 .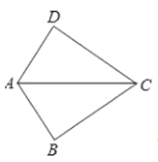 14. 已知a、b、c是 的三边长,且满足关系 ,则 的形状为 .15. 如图,△ABC≌△DEF,点A与D,B与E分别是对应顶点,且测得BC=5cm,BF=7cm,则EC长为cm.
14. 已知a、b、c是 的三边长,且满足关系 ,则 的形状为 .15. 如图,△ABC≌△DEF,点A与D,B与E分别是对应顶点,且测得BC=5cm,BF=7cm,则EC长为cm.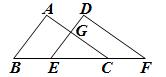 16. 如图, °.
16. 如图, °.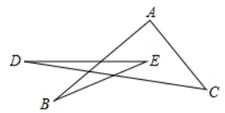 17. 如图, 的平分线相交于点 ,则∠P1与∠A数量关系是; 的平分线相交于点 , , 的平分线相交于点 ……以此类推,则 的度数是(用含 与 的代数式表示).
17. 如图, 的平分线相交于点 ,则∠P1与∠A数量关系是; 的平分线相交于点 , , 的平分线相交于点 ……以此类推,则 的度数是(用含 与 的代数式表示).
三、解答题
-
18. 如图,已知 , .求证: .
 19. 如图,点B,F,C,E在同一直线上,AC,DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=CE.求证: .
19. 如图,点B,F,C,E在同一直线上,AC,DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=CE.求证: .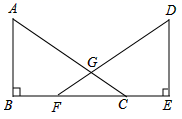 20. 如图,D是△ABC中BC边上一点,∠C=∠DAC.
20. 如图,D是△ABC中BC边上一点,∠C=∠DAC.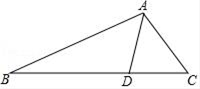
(1)、尺规作图:作∠ADB的平分线,交AB于点E(保留作图痕迹,不写作法);(2)、在(1)的条件下,求证:DE∥AC.
21. 如图,DE⊥AB于E , DF⊥AC于F , 若BD=CD , BE=CF .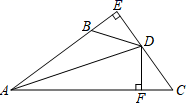 (1)、求证:AD平分∠BAC .(2)、写出AB+AC与AE之间的等量关系,并说明理由.22. 如图,AC //BD,AC =BD,
(1)、求证:AD平分∠BAC .(2)、写出AB+AC与AE之间的等量关系,并说明理由.22. 如图,AC //BD,AC =BD, (1)、求证:AD //BC.(2)、在AB上取两点E、F,AE =BF.请你判断DE、CF 有何关系?并说明理由.23. 如图,已知AB⊥AD,AC⊥AE,AB=AD,AC=AE,BC分别交AD、DE于点G、F,AC与DE交于点H.
(1)、求证:AD //BC.(2)、在AB上取两点E、F,AE =BF.请你判断DE、CF 有何关系?并说明理由.23. 如图,已知AB⊥AD,AC⊥AE,AB=AD,AC=AE,BC分别交AD、DE于点G、F,AC与DE交于点H.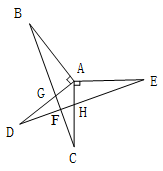 (1)、求证:△ABC≌△ADE;(2)、求证:BC⊥DE.24. 探究与运用
(1)、求证:△ABC≌△ADE;(2)、求证:BC⊥DE.24. 探究与运用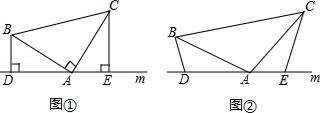 (1)、探究:如图①,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥m于点D,CE⊥m于点E,求证:△ABD≌△CAE.(2)、应用:如图②,在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC,求证:DE=BD+CE.25. 如图1所示,已知点 在直线 上,点 , 在直线 上,且 , 平分 .
(1)、探究:如图①,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥m于点D,CE⊥m于点E,求证:△ABD≌△CAE.(2)、应用:如图②,在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC,求证:DE=BD+CE.25. 如图1所示,已知点 在直线 上,点 , 在直线 上,且 , 平分 .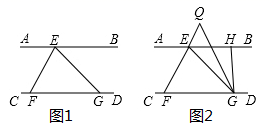 (1)、判断直线 与直线 是否平行,并说明理由.(2)、如图2所示, 是 上点 右侧一动点, 的平分线 交 的延长线于点 ,设 , .
(1)、判断直线 与直线 是否平行,并说明理由.(2)、如图2所示, 是 上点 右侧一动点, 的平分线 交 的延长线于点 ,设 , .①若 , ,求 的度数.
②判断:点 在运动过程中, 和 的数量关系是否发生变化?若不变,求出 和 的数量关系;若变化,请说明理由.