湘教版九年级上册初中数学期中复习专题3反比例函数的应用
试卷更新日期:2021-10-25 类型:期中考试
一、单选题
-
1. 某气球内充满了一定质量 的气体,当温度不变时,气球内气体的气压 (单位: )是气体体积 (单位: )的反比例函数: ,能够反映两个变量 和 函数关系的图象是( )A、
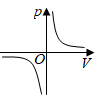 B、
B、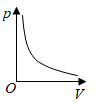 C、
C、 D、
D、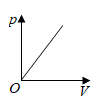 2. 已知蓄电池的电压为定值,使用蓄电池时,电流O(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.下列说法正确的是( )
2. 已知蓄电池的电压为定值,使用蓄电池时,电流O(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.下列说法正确的是( )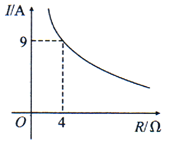 A、函数解析式为I= B、蓄电池的电压是18V C、当I≤10A时,R≥3.6Ω D、当R=6Ω时,I=4A3. 购买 斤水果需 元,购买一斤水果的单价 与 的关系式是( )A、 B、 ( 为自然数) C、 ( 为整数) D、 ( 为正整数)4. 某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为 的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度 随时间 (小时)变化的函数图象,其中 段是双曲线 的一部分,则当 时,大棚内的温度约为( )
A、函数解析式为I= B、蓄电池的电压是18V C、当I≤10A时,R≥3.6Ω D、当R=6Ω时,I=4A3. 购买 斤水果需 元,购买一斤水果的单价 与 的关系式是( )A、 B、 ( 为自然数) C、 ( 为整数) D、 ( 为正整数)4. 某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为 的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度 随时间 (小时)变化的函数图象,其中 段是双曲线 的一部分,则当 时,大棚内的温度约为( ) A、 B、 C、 D、5. 蓄电池的电压为定值.使用此电源时,用电器的电流 ( )与电阻 ( )之间的函数关系如图所示,如果以此蓄电池为电源的用电器限制电流不得超过 ,那么用电器的可变电阻应控制在( )范围内.
A、 B、 C、 D、5. 蓄电池的电压为定值.使用此电源时,用电器的电流 ( )与电阻 ( )之间的函数关系如图所示,如果以此蓄电池为电源的用电器限制电流不得超过 ,那么用电器的可变电阻应控制在( )范围内. A、 B、 C、 D、6. 近似眼镜的度数 (度)与镜片焦距 (米)之间具有如图所示的反比例函数关系,若要配制一副度数小于400度的近似眼镜,则镜片焦距 的取值范围是( )
A、 B、 C、 D、6. 近似眼镜的度数 (度)与镜片焦距 (米)之间具有如图所示的反比例函数关系,若要配制一副度数小于400度的近似眼镜,则镜片焦距 的取值范围是( )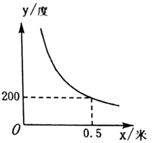 A、0米 米 B、 米 C、0米 米 D、 米7. 如果以 的速度向水箱注水,5h可以注满.为了赶时间,现增加进水管,使进水速度达到 ,那么此时注满水箱所需要的时间 与 之间的函数关系式为( )A、 B、 C、 D、8. 已知甲,乙两地相距 (单位: ),汽车从甲地匀速行驶到乙地,则汽车行驶的时间 (单位: )关于行驶速度 (单位: )的函数图象是( )A、
A、0米 米 B、 米 C、0米 米 D、 米7. 如果以 的速度向水箱注水,5h可以注满.为了赶时间,现增加进水管,使进水速度达到 ,那么此时注满水箱所需要的时间 与 之间的函数关系式为( )A、 B、 C、 D、8. 已知甲,乙两地相距 (单位: ),汽车从甲地匀速行驶到乙地,则汽车行驶的时间 (单位: )关于行驶速度 (单位: )的函数图象是( )A、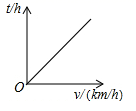 B、
B、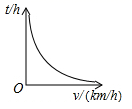 C、
C、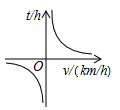 D、
D、 9. 如图,是一个闭合电路,其电源电压为定值,电流 是电阻 的反比例函数,当 时, ,若电阻 增大 ,则电流 为( )
9. 如图,是一个闭合电路,其电源电压为定值,电流 是电阻 的反比例函数,当 时, ,若电阻 增大 ,则电流 为( ) A、 B、 C、 D、10. 阿基米德说:“给我一个支点,我就能撬动整个地球”这句话精辟地阐明了一个重要的物理学知识——杠杆原理,即“阻力×阻力臂=动力×动力臂”.若已知某一杠杆的阻力和阻力臂分别为 和 ,则这一杠杆的动力 和动力臂 之间的函数图象大致是( )
A、 B、 C、 D、10. 阿基米德说:“给我一个支点,我就能撬动整个地球”这句话精辟地阐明了一个重要的物理学知识——杠杆原理,即“阻力×阻力臂=动力×动力臂”.若已知某一杠杆的阻力和阻力臂分别为 和 ,则这一杠杆的动力 和动力臂 之间的函数图象大致是( ) A、
A、 B、
B、 C、
C、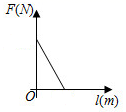 D、
D、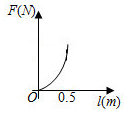
二、填空题
-
11. 一定质量的氧气,它的密度ρ(kg/m3)是它的体积V(m3)的反比例函数,当V=100m3时,ρ=1.4kg/m3;那么当V=2m3时,氧气的密度为kg/m3.12. 小宇每天骑自行车上学,从家到学校所需时间 (分)与骑车速度 (千米/分)关系如图所示.一天早上,由于起床晚了,为了不迟到,需不超过 分钟赶到学校,那么他骑车的速度至少是千米/分.
 13. 在温度不变的条件下,一定质量的气体的压强p与它的体积V成反比例,当V=200时,p=50,则当p=25时,V= .14.
13. 在温度不变的条件下,一定质量的气体的压强p与它的体积V成反比例,当V=200时,p=50,则当p=25时,V= .14.如图,双曲线y= (k>0)与⊙O在第一象限内交于P、Q两点,分别过P、Q两点向x轴和y轴作垂线.已知点P坐标为(1,3),则图中阴影部分的面积为 .
 15. 近视眼镜的度数y(度)与镜片焦距x(m)成反比例,已知500度的近视眼镜镜片的焦距是0.2m,则y与x之间的函数关系式是16.
15. 近视眼镜的度数y(度)与镜片焦距x(m)成反比例,已知500度的近视眼镜镜片的焦距是0.2m,则y与x之间的函数关系式是16.如图,直线y=﹣3x+3与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线(k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线(k≠0)上的点D1处,则a= .
 17. 把一个长、宽、高分别为3cm,2cm,1cm的长方体铜块铸成一个圆柱体铜块,则该圆柱体铜块的底面积s(cm2)与高h(cm)之间的函数关系式为 .
17. 把一个长、宽、高分别为3cm,2cm,1cm的长方体铜块铸成一个圆柱体铜块,则该圆柱体铜块的底面积s(cm2)与高h(cm)之间的函数关系式为 .
三、解答题
-
18. 小明在某一次实验中,测得两个变量之间的关系如下表所示:
x
1
2
3
4
12
y
12.03
5.98
3.03
1.99
1.00
请你根据表格回答下列问题:
①这两个变量之间可能是怎样的函数关系?你是怎样作出判断的?请你简要说明理由;
②请你写出这个函数的解析式;
③表格中空缺的数值可能是多少?请你给出合理的数值.
19. 某电器商场销售甲、乙两种品牌空调,已知每台乙种品牌空调的进价比每台甲种品牌空调的进价高20%,用7200元购进的乙种品牌空调数量比用3000元购进的甲种品牌空调数量多2台.(1)、求甲、乙两种品牌空调的进货价;(2)、该商场拟用不超过16000元购进甲、乙两种品牌空调共10台进行销售,其中甲种品牌空调的售价为2500元/台,乙种品牌空调的售价为3500元/台.请您帮该商场设计一种进货方案,使得在售完这10台空调后获利最大,并求出最大利润.20.在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:
如果矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形.例如,下图中的矩形A1B1C1D1 , A2B2C2D2 , AB3C3D3都是点A,B,C的覆盖矩形,其中矩形AB3C3D3是点A,B,C的最优覆盖矩形.
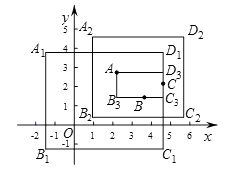
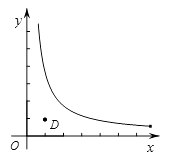 (1)、已知A( 2,3),B(5,0),C( , 2).
(1)、已知A( 2,3),B(5,0),C( , 2).①当 时,点A,B,C的最优覆盖矩形的面积为;
②若点A,B,C的最优覆盖矩形的面积为40,则t的值为;
(2)、已知点D(1,1),点E( , ),其中点E是函数 的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.21. 某地上年度电价为0.8元,年用电量为1亿度,本年度计划将电价调至0.55~0.75元之间,经测算,若电价调至x元,则本年度新增用电量y(亿度)与(x﹣0.4)元成反比例.又当x=0.65元时,y=0.8.(1)求y与x之间的函数关系式.
(2)若每度电的成本价为0.3元,则电价调至多少时本年度电力部门的收益将比上年度增加20%?(收益=用电量×(实际电价﹣成本价))
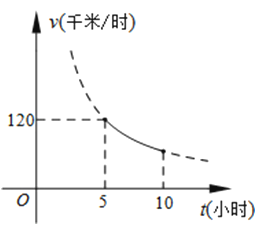
22.一辆客车从甲地出发前往乙地,平均速度v(千米/小时)与所用时间t(小时)的函数关系如图所示,其中60≤v≤120.
(1)直接写出v与t的函数关系式;
(2)若一辆货车同时从乙地出发前往甲地,客车比货车平均每小时多行驶20千米,3小时后两车相遇.
①求两车的平均速度;
②甲、乙两地间有两个加油站A、B,它们相距200千米,当客车进入B加油站时,货车恰好进入A加油站(两车加油的时间忽略不计),求甲地与B加油站的距离.
四、综合题
-
23. 为了做好校园疫情防控工作,校医每天早上对全校办公室和教室进行药物喷洒消毒,她完成3间办公室和2间教室的药物喷洒要19min;完成2间办公室和1间教室的药物喷洒要11min.
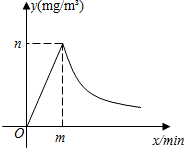 (1)、校医完成一间办公室和一间教室的药物喷洒各要多少时间?(2)、消毒药物在一间教室内空气中的浓度y(单位:mg/m3)与时间x(单位:min)的函数关系如图所示:校医进行药物喷洒时y与x的函数关系式为y=2x,药物喷洒完成后y与x成反比例函数关系,两个函数图象的交点为A(m,n).当教室空气中的药物浓度不高于1mg/m3时,对人体健康无危害,校医依次对一班至十一班教室(共11间)进行药物喷洒消毒,当她把最后一间教室药物喷洒完成后,一班学生能否进入教室?请通过计算说明.24. 小明同学训练某种运算技能,每次训练完成相同数量的题目,各次训练题目难度相当. 当训练次数不超过15次时,完成一次训练所需要的时间y(单位:秒)与训练次数x(单位:次)之间满足如图所示的反比例函数关系. 完成第3次训练所需时间为400秒.
(1)、校医完成一间办公室和一间教室的药物喷洒各要多少时间?(2)、消毒药物在一间教室内空气中的浓度y(单位:mg/m3)与时间x(单位:min)的函数关系如图所示:校医进行药物喷洒时y与x的函数关系式为y=2x,药物喷洒完成后y与x成反比例函数关系,两个函数图象的交点为A(m,n).当教室空气中的药物浓度不高于1mg/m3时,对人体健康无危害,校医依次对一班至十一班教室(共11间)进行药物喷洒消毒,当她把最后一间教室药物喷洒完成后,一班学生能否进入教室?请通过计算说明.24. 小明同学训练某种运算技能,每次训练完成相同数量的题目,各次训练题目难度相当. 当训练次数不超过15次时,完成一次训练所需要的时间y(单位:秒)与训练次数x(单位:次)之间满足如图所示的反比例函数关系. 完成第3次训练所需时间为400秒.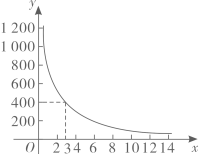 (1)、求y与x之间的函数关系式;(2)、当x的值为6,8,10时,对应的函数值分别为y1 , y2 , y3 , 比较(y1-y2)与(y2-y3)的大小: y1-y2y2-y3.25. 某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把1200立方米的生活垃圾运走:(1)、假如每天能运x立方米,所需时间为y天,写出y与x之间的函数表达式;
(1)、求y与x之间的函数关系式;(2)、当x的值为6,8,10时,对应的函数值分别为y1 , y2 , y3 , 比较(y1-y2)与(y2-y3)的大小: y1-y2y2-y3.25. 某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把1200立方米的生活垃圾运走:(1)、假如每天能运x立方米,所需时间为y天,写出y与x之间的函数表达式;
(2)、若每辆拖拉机一天能运12立方米,则5辆这样的拖拉机要用多少天才能运完?
(3)、在(2)的情况下,运了8天后,剩下的任务要在不超过6天的时间内完成,那么至少需要增加多少辆这样的拖拉机才能按时完成任务?26. 知识背景,当a>0且x>0时,因为 ,所以 ,从而(当x= 时取等号).
设函数y=x+ (a>0,x>0),由上述结论可知:当x= 时,该函数有最小值为2 .
应用举例
已知函数为y1=x(x>0)与函数 (x>0),则当x= =2时,y1+y2=x+ 有最小值为2 =4.
解决问题
(1)、已知函数为y1=x+3(x>﹣3)与函数y2=(x+3)2+9(x>﹣3),当x取何值时, 有最小值?最小值是多少?(2)、已知某设备租赁使用成本包含以下三部分:一是设备的安装调试费用,共490元;二是设备的租赁使用费用,每天200元;三是设备的折旧费用,它与使用天数的平方成正比,比例系数为0.001.若设该设备的租赁使用天数为x天,则当x取何值时,该设备平均每天的租货使用成本最低?最低是多少元?27. 某公司从2014年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:年 度
2013
2014
2015
2016
投入技改资金x(万元)
2.5
3
4
4.5
产品成本y(万元/件)
7.2
6
4.5
4
(1)、请你认真分析表中数据,从一次函数和反比例函数中确定哪一个函数能表示其变化规律,给出理由,并求出其解析式;(2)、按照这种变化规律,若2017年已投入资金5万元.①预计生产成本每件比2016年降低多少万元?
②若打算在2017年把每件产品成本降低到3.2万元,则还需要投入技改资金多少万元?(结果精确到0.01万元).
28. 我市某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15﹣20℃的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚里温度y(℃)随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线y= 的一部分,请根据图中信息解答下列问题: (1)、求k的值;(2)、恒温系统在一天内保持大棚里温度在15℃及15℃以上的时间有多少小时?
(1)、求k的值;(2)、恒温系统在一天内保持大棚里温度在15℃及15℃以上的时间有多少小时?