2021年秋季浙教版数学九年级上学期期中测试模拟卷（适合绍兴、台州、义乌地区）

试卷更新日期：2021-10-25 类型：期中考试

进入出卷网下载

一、单选题

1. 当 $x \geq 2$ 时，二次函数 $y = x^{2} - 2 x - 3$ 有（）

A、最大值-3 B、最小值-3 C、最大值-4 D、最小值-4

查看试题解析
2. 一个不透明的盒子里有若干个黑球和3个白球，3个红球，它们除颜色外没有其他区别，若从这个盒子里随机摸出一个黑球的概率是 $\frac{3}{5}$ ，则这个盒子里黑球的个数为（）

A、12个 B、9个 C、6个 D、3个

查看试题解析
3. 已知点 $(- 3, y_{1})$ ， $(5, y_{2})$ 在二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象上，点 $(x_{0}, y_{0})$ 是函数图象的顶点，则（）

A、当 $y_{0} \geq y_{1} > y_{2}$ 时， $x_{0}$ 的取值范围是 $x_{0} < - 3$ B、当 $y_{0} \geq y_{1} > y_{2}$ 时， $x_{0}$ 的取值范围是 $x_{0} < 1$ C、当 $y_{1} > y_{2} \geq y_{0}$ 时， $x_{0}$ 的取值范围是 $1 < x_{0} < 5$ D、当 $y_{1} > y_{2} \geq y_{0}$ 时， $x_{0}$ 的取值范围是 $x_{0} > 5$

查看试题解析
4. 将抛物线y=x²向右平移1个单位长度后，所得到的抛物线的解析式是（）

A、y=x²-1 B、y=x²-1 C、y=(x-1)² D、y=(x+1)²

查看试题解析
5. 二次函数 $y = a x^{2} + b x + c$ （ $a$ 、 $b$ 、 $c$ 是常数，且 $a \neq 0$ ）的自变量 $x$ 与函数值 $y$ 的部分对应值如下表：

$x$

…

$- 1$

0

1

2

…

$y$

…

$m$

2

2

$n$

…

且当 $x = \frac{3}{2}$ 时，对应的函数值 $y < 0$ .有以下结论：① $a b c > 0$ ；② $m + n < - \frac{20}{3}$ ；③关于 $x$ 的方程 $a x^{2} + b x + c = 0$ 的负实数根在 $- \frac{1}{2}$ 和0之间；④ $P_{1} (t - 1 ， y_{1})$ 和 $P_{2} (t + 1 ， y_{2})$ 在该二次函数的图象上，则当实数 $t > \frac{1}{3}$ 时， $y_{1} > y_{2}$ .其中正确的结论是（）

A、①② B、②③ C、③④ D、②③④

查看试题解析
6. $A B = 12 c m$ ，过 $A$ 、 $B$ 两点画半径为 $6 c m$ 的圆，能画的圆的个数为（）

A、0个 B、1个 C、2个 D、无数个

查看试题解析
7. 如图所示，中堂中学教学楼前喷水池喷出的抛物线形水柱，水柱喷出的竖直高度y（m）与水平距离x（m）满足y＝﹣（x﹣2）²+6，则水柱的最大高度是（　　）

A、2 B、4 C、6 D、2+ $\sqrt{6}$

查看试题解析
8. 已知 $⊙ O_{1}$ ， $⊙ O_{2}$ ， $⊙ O_{3}$ 是等圆， $△ A B P$ 内接于 $⊙ O_{1}$ ，点C ， E分别在 $⊙ O_{2}$ ， $⊙ O_{3}$ 上．如图，①以C为圆心， $A P$ 长为半径作弧交 $⊙ O_{2}$ 于点D ，连接 $C D$ ；②以E为圆心， $B P$ 长为半径作弧交 $⊙ O_{3}$ 于点F ，连接 $E F$ ；下面有四个结论：① $C D + E F = A B$ ；② $\overset{⌢}{C D} + \overset{⌢}{E F} = \overset{⌢}{A B}$ ；③ $∠ C O_{2} D + ∠ E O_{3} F = ∠ A O_{1} B$ ；④ $∠ C D O_{2} + ∠ E F O_{3} = ∠ P$ ，所有正确结论的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 如图，一次函数 $y_{1} = - x$ 与二次函数为 $y_{2} = a x^{2} + b x + c$ 的图象相交于点M，N，则关于x的一元二次方程 $a x^{2} + (b + 1) x + c = 0$ 的根的情况是（）

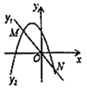A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、有两个实数根

查看试题解析
10. 如图，是反比例函数 $y = \frac{4}{x} (x > 0)$ 图象，阴影部分表示它与横纵坐标轴正半轴围成的区域，在该区域内 $($ 不包括边界 $)$ 的整数点个数是k，则抛物线 $y = - {(x - 2)}^{2} - 2$ 向上平移k个单位后形成的图象是 $($ 　　 $)$

A、 B、 C、 D、

查看试题解析

二、填空题

11. 若 $\frac{x}{3} = \frac{y}{5} = \frac{z}{7}$ ，则 $\frac{x - y + z}{x + y - z}$ =.

查看试题解析

12. 在就地过年倡议下，更多游客缩小出游半径，本地游、近郊游、周边游取代异地长线游，成为牛年出行新趋势．某地区对近郊游的住宿环境、餐饮、服务等方面对所住游客进行了综合满意度调查，在甲，乙两个景点都去过的的游客中随机抽取了100人，每人分别对这两个景点进行了评分，统计如下：

	非常满意	较满意	一般	不太满意	非常不满意	合计
甲	28	40	10	10	12	100
乙	25	20	45	6	4	100

若小聪要在甲，乙两个景点中选择一个景点，根据表格中数据，你建议她去景点（填甲或乙），理由是．

查看试题解析

13. 在⊙O中，AB是直径，AB＝2，C是圆上除A、B外的一点，D、E分别是 $\overset{⌢}{A C}$ 、 $\overset{⌢}{B C}$ 的中点，M是弦DE的中点，则CM的取值范围是.

查看试题解析
14. 如图Rt△ABC ， ∠C＝90°，分别以各边为直径作半圆，图中阴影部分在数学史上称为“希波克拉底月牙”：当AC＝3，BC＝4时，则阴影部分的面积为．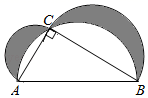

查看试题解析
15. 如图所示，在⊙O中，AB为弦，OC⊥AB交AB于点D，且OD=DC，P为⊙O上任意一点，连接PA，PB，若⊙O的半径为1，则S_△_PAB的最大值为.

查看试题解析
16. 定义：在平面直角坐标系中，我们将横、纵坐标都是整数的点称为“整点”.若抛物线y＝ax²﹣2ax+a+3与x轴围成的区域内(不包括抛物线和x轴上的点)恰好有8个“整点”，则a的取值范围是.

查看试题解析

三、解答题

17. 已知二次函数y=x²+3x+m的图象与x轴交于点A（﹣4，0）．

(1)、求m的值；

(2)、求该函数图象与坐标轴其余交点的坐标．

查看试题解析
18. 袋中有1个红球和2个黑球，这些球除颜色外都相同.小明做摸球实验：他搅匀后从中任意摸出1个球，记录颜色后放回、搅匀，再从中任意摸出1球.像这样连续摸两次算一次实验.若摸出红球得2分，摸出黑球得1分.

(1)、求两次摸球所得总分是4分的概率；

(2)、若要使每次摸球实验所得总分不少于3分，如何改变袋中球的情况？

查看试题解析
19. 已知二次函数 $y = x^{2} + b x + c$ 的图象如图所示，它与x轴的一个交点的坐标为（－1，0），与y轴的交点坐标为（0，－3）

(1)、求此二次函数的解析式；

(2)、求此二次函数的图象与x轴的另一个交点的坐标

(3)、根据图象回答：当x取何值时，y＜0？

查看试题解析
20. 已知在Rt△ABC中，∠ACB=90°，现按如下步骤作图：
①分别以A，C为圆心，a为半径（a＞ $\frac{1}{2}$ AC）作弧，两弧分别交于M，N两点；
②过M，N两点作直线MN交AB于点D，交AC于点E；
③将△ADE绕点E顺时针旋转180°，设点D的像为点F．

(1)、请在图中直线标出点F并连接CF；

(2)、求证：四边形BCFD是平行四边形；

(3)、当∠B为多少度时，四边形BCFD是菱形．

查看试题解析
21. 某河上有抛物线形拱桥，当水面离拱顶5m时，水面宽8m．一木船宽4m，高2m，载货后，木船露出水面的部分为 $\frac{3}{4}$ m．以拱顶O为坐标原点建立如图所示的平面直角坐标系，A、B为抛物线与水面的交点．

(1)、B点的坐标为；

(2)、求抛物线解析式；

(3)、当水面离拱顶1.8米时，木船能否通过拱桥？

查看试题解析
22. 某超市销售一种商品，每件成本为50元，销售人员经调查发现，销售单价为100元时，每月的销售量为50件，而销售单价每降低2元，则每月可多售出10件，且要求销售单价不得低于成本．

(1)、求该商品每月的销售量y（件）与销售单价x（元）之间的函数关系式；（不需要求自变量取值范围）

(2)、若使该商品每月的销售利润为4000元，并使顾客获得更多的实惠，销售单价应定为多少元？

(3)、超市的销售人员发现：当该商品每月销售量超过某一数量时，会出现所获利润反而减小的情况，为了每月所获利润最大，该商品销售单价应定为多少元？

查看试题解析
23. 我们知道：有一内角为直角的三角形叫做直角三角形.类似地，我们定义：有一内角为45°的三角形叫做半直角三角形.如图，在平面直角坐标系中，O为原点，A(4，0)，B(﹣4，0)，D是y轴上的一个动点，∠ADC=90°(A、D、C按顺时针方向排列)，BC与经过A、B、D三点的⊙M交于点E，DE平分∠ADC，连结AE，BD.显然△DCE、△DEF、△DAE是半直角三角形.

(1)、求证：△ABC是半直角三角形；

(2)、求证：∠DEC=∠DEA；

(3)、若点D的坐标为(0，8)，求AE的长.

查看试题解析
24. 如图，二次函数 $y = - x^{2} - 2 x + 4 - a^{2}$ 的图象与一次函数 $y = - 2 x$ 的图象交于点 $A$ 、 $B$ （点 $B$ 在右侧），与 $y$ 轴交于点 $C$ ，点 $A$ 的横坐标恰好为 $a$ .动点 $P$ 、 $Q$ 同时从原点 $O$ 出发，沿射线 $O B$ 分别以每秒 $\sqrt{5}$ 和 $2 \sqrt{5}$ 个单位长度运动，经过 $t$ 秒后，以 $P Q$ 为对角线作矩形 $P M Q N$ ，且矩形四边与坐标轴平行.

(1)、求 $a$ 的值及 $t = 1$ 秒时点 $P$ 的坐标；

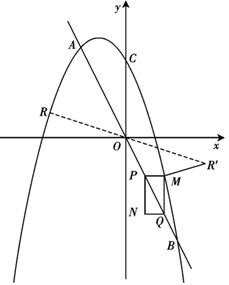(2)、当矩形 $P M Q N$ 与抛物线有公共点时，求时间 $t$ 的取值范围；

(3)、在位于 $x$ 轴上方的抛物线图象上任取一点 $R$ ，作关于原点 $(0 ， 0)$ 的对称点为 $R'$ ，当点 $M$ 恰在抛物线上时，求 $R' M$ 长度的最小值，并求此时点 $R$ 的坐标.

查看试题解析

$x$	…	$- 1$	0	1	2	…
$y$	…	$m$	2	2	$n$	…