2021年秋季浙教版数学九年级上学期期中测试模拟卷(适合宁波地区)
试卷更新日期:2021-10-25 类型:期中考试
一、单选题
-
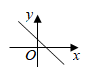
1. 若 ,则 的值为( )A、 B、 C、 D、2. 下列事件中是不可能事件的为( )A、抛掷一石头,石头终将落地 B、从装有黑球、白球的袋里摸出红球 C、地球绕着太阳转 D、买1张彩票,中 万大奖3. 二次函数 的顶点坐标是( )A、(1,-3) B、(-1,-3) C、(1,3) D、(-1,3)4. 一次函数 的图象如图所示,则二次函数 的图象可能是( )
 A、
A、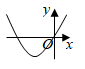 B、
B、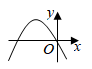 C、
C、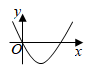 D、
D、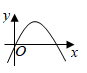 5. 若扇形的半径为3,圆心角为60°,则此扇形的弧长是( )A、π B、 2π C、 3π D、4π6. 如图, 内接于 , ,点 是边 的中点,连接 并延长交 于点 ,连接 ,则 的大小为( )
5. 若扇形的半径为3,圆心角为60°,则此扇形的弧长是( )A、π B、 2π C、 3π D、4π6. 如图, 内接于 , ,点 是边 的中点,连接 并延长交 于点 ,连接 ,则 的大小为( )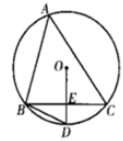 A、55° B、65° C、70° D、75°7. 如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,BC,则∠C的度数是( )
A、55° B、65° C、70° D、75°7. 如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,BC,则∠C的度数是( )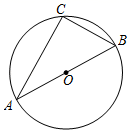 A、60° B、90° C、120° D、150°8. 已知二次函数y=ax2+bx+c的图像如图所示,那么abc,b2 -4ac,2a+b,a+b+c这四个代数式中,值为正数的有( )
A、60° B、90° C、120° D、150°8. 已知二次函数y=ax2+bx+c的图像如图所示,那么abc,b2 -4ac,2a+b,a+b+c这四个代数式中,值为正数的有( )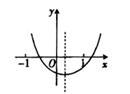 A、4个 B、3个 C、2个 D、1个9. 《九章算术》第一章“方田”中讲述了扇形面积的计算方法:“今有宛田,下周三十步,径十六步,问为田几何?”大致意思为:现有一块扇形的田,弧长30步,其所在圆的直径是16步,则这块田面积为( )A、 平方步 B、 平方步 C、120平方步 D、240平方步10. 如图,AB是⊙O的直径,点D,C在⊙O上,∠DOC=90°,AD= ,BC=1,则⊙O的半径为( )
A、4个 B、3个 C、2个 D、1个9. 《九章算术》第一章“方田”中讲述了扇形面积的计算方法:“今有宛田,下周三十步,径十六步,问为田几何?”大致意思为:现有一块扇形的田,弧长30步,其所在圆的直径是16步,则这块田面积为( )A、 平方步 B、 平方步 C、120平方步 D、240平方步10. 如图,AB是⊙O的直径,点D,C在⊙O上,∠DOC=90°,AD= ,BC=1,则⊙O的半径为( )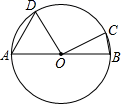 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 一幅比例尺为 的地图上,某道路的长度为 ,则它的实际长度为 .12. 一只盒子中有红球m个,白球8个,黑球n个,每个球除颜色外都相同,从中任取一个球,如果取得红球或黑球的概率与取得白球的概率相同,那么m与n的关系是.13. 二次函数y=ax²+bx+c图象上部分点的横坐标x,纵坐标y的对应值如下表:
x
…
﹣2
﹣1
0
1
2
…
m
…
y
…
0
4
6
6
4
…
﹣6
…
则这个二次函数的对称轴为直线x= , m=(m>0).
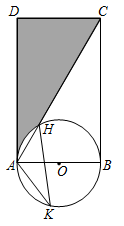
14. 古希腊时期,人们认为最美人体的肚脐至脚底的长度与身高长度之比是 ( 0.618,称之为黄金分割比例),著名的“断臂维纳斯”便是如此,若某位女性身高为165cm , 肚脐到头顶高度为65cm , 则其应穿鞋跟为cm的高跟鞋才能使人体近似满足黄金分割比例.(精确到1cm)15. 如图抛物线y=ax2+bx+c的对称轴是x=﹣1,与x轴的一个交点为(﹣5,0),则不等式ax2+bx+c>0的解集为 . 16. 如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第23秒时,点E在量角器上对应的度数是度.
16. 如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第23秒时,点E在量角器上对应的度数是度.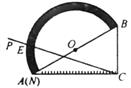
三、解答题
-
17. (1)已知a、b、c、d是成比例线段,其中a=3cm,b=2cm,c=6cm,求线段d的长.
(2)已知线段a、b、c,a=4cm,b=9cm,线段c是线段a和b的比例中项.求线段c的长.
18. 如图,在正方形网格中,△ABC的顶点在格点上.请仅用无刻度直尺完成以下作图(保留作图痕迹).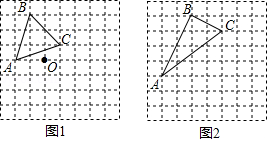
( 1 )在图1中,作 关于点O对称的 ;
( 2 )在图2中,作 绕点A顺时针旋转一定角度后,顶点仍在格点上的 .
19. 这是一个两人转盘游戏,准备加图三个可以自由转动的转盘,甲、乙两人中甲分别转动三个转盘,乙记录指针停下时所指的数字,当三个转盘的数字中有数字相同时,就算甲赢,否则就算乙赢.
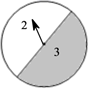
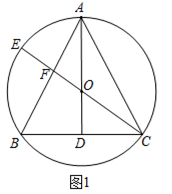
 (1)、画树状图计算甲赢的概率;(2)、请判断这个游戏是否公平,如果不公平,请修改规则,使之公平.20. 设二次函数y=(x-m)(x-m-2),其中m为实数.(1)、若函数y的图象经过点A(4,3),求函数y的表达式.(2)、若函数y的图象的对称轴是直线x=1,求该函数的最小值.(3)、把函数y的图象向上平移k个单位,所得图象与x轴没有交点,求证:k>1.21. 如图, 内接于 ,且 , 是 上的一点, 在 的延长线上,连结 交 于 ,连结 .
(1)、画树状图计算甲赢的概率;(2)、请判断这个游戏是否公平,如果不公平,请修改规则,使之公平.20. 设二次函数y=(x-m)(x-m-2),其中m为实数.(1)、若函数y的图象经过点A(4,3),求函数y的表达式.(2)、若函数y的图象的对称轴是直线x=1,求该函数的最小值.(3)、把函数y的图象向上平移k个单位,所得图象与x轴没有交点,求证:k>1.21. 如图, 内接于 ,且 , 是 上的一点, 在 的延长线上,连结 交 于 ,连结 .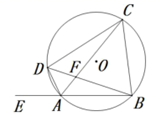 (1)、求证: 平分 ;(2)、若 ,求证: .22. 某商店将成本为每件60元的某商品标价100元出售.(1)、为了促销,该商品经过两次降低后每件售价为81元,若两次降价的百分率相同,求每次降价的百分率(2)、经调查,该商品每降价1元,每月可多售出5件,若该商品按原标价出售,每月可销售100件,那么当销售价为多少元时,可以使该商品的月利润最大?最大的月利润是多少?
(1)、求证: 平分 ;(2)、若 ,求证: .22. 某商店将成本为每件60元的某商品标价100元出售.(1)、为了促销,该商品经过两次降低后每件售价为81元,若两次降价的百分率相同,求每次降价的百分率(2)、经调查,该商品每降价1元,每月可多售出5件,若该商品按原标价出售,每月可销售100件,那么当销售价为多少元时,可以使该商品的月利润最大?最大的月利润是多少?