2021年秋季浙教版数学九年级上学期期中测试模拟卷（适合嘉兴、舟山、金华、丽水、湖州、衢州地区）

试卷更新日期：2021-10-25 类型：期中考试

进入出卷网下载

一、单选题

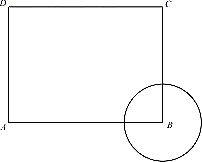
1. 一个不透明的盒子中装有1白球和200个黑球，它们除了颜色外都相同，将球搅匀，从中任意摸出一个球，摸到黑球是（）

A、必然事件 B、随机事件 C、不可能事件 D、以上事件都有可能

查看试题解析
2. 已知二次函数的解析式为y=3（x-1）²-3，则该二次函数图象的顶点坐标是（）

A、（1，-3） B、（-1，-3） C、（1，3） D、（-1，3）

查看试题解析
3. 如图，已知长方形 $A B C D$ 中， $A B = 4 ， A D = 3$ ，圆B的半径为1，圆A与圆B内切，则点 $C ， D$ 与圆A的位置关系是（）

A、点C在圆A外，点D在圆A内 B、点C在圆A外，点D在圆A外 C、点C在圆A上，点D在圆A内 D、点C在圆A内，点D在圆A外

查看试题解析
4. 小明计划到永州市体验民俗文化，想从“零陵渔鼓、瑶族长鼓舞、东安武术、舜帝祭典”四种民俗文化中任意选择两项，则小明选择体验“瑶族长鼓舞、舜帝祭典”的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{3}{4}$ D、 $\frac{1}{6}$

查看试题解析
5. 二次函数 $y = x^{2} + 3 x + 2$ 图象平移后经过点 $(2, 18)$ ，则下列可行的平移方法是（）

A、向右平移1个单位，向上平移2个单位 B、向右平移1个单位，向下平移2个单位 C、向左平移1个单位，向上平移2个单位 D、向左平移1个单位，向下平移2个单位

查看试题解析
6. 若扇形的半径为3，圆心角为60°，则此扇形的弧长是（）

A、 $\frac{1}{2}$ π B、π C、 $\frac{3}{2}$ π D、2π

查看试题解析
7. 已知点 $A (- 2 ， y_{1})$ ， $B (- 1 ， y_{2})$ ， $C (5 ， y_{3})$ 都在二次函数 $y = - x^{2} + 2 x + k$ 的图象上，则（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{3} < y_{2} < y_{1}$ C、 $y_{3} < y_{1} < y_{2}$ D、 $y_{2} < y_{1} < y_{3}$

查看试题解析
8. P为⊙O内一点， $O P = 3$ ，⊙O半径为5，则经过P点的最短弦长为（）

A、5 B、6 C、8 D、10

查看试题解析
9. 如图，正六边形ABCDEF内接于 $⊙ O$ ，过点O作 $O M ⊥$ 弦BC于点M ，若 $⊙ O$ 的半径为4，则弦心距OM的长为（）

A、 $2 \sqrt{3}$ B、 $\sqrt{3}$ C、2 D、 $2 \sqrt{2}$

查看试题解析
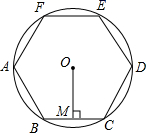10. 已知二次函数 $y = a x^{2} - 2 a x - 3 a (a \neq 0)$ ，关于此函数的图象及性质，下列结论中不一定成立的是（）

A、该图象的顶点坐标为 $(1 ， - 4 a)$ B、该图象与 $x$ 轴的交点为 $(- 1 ， 0) ， (3 ， 0)$ C、若该图象经过点 $(- 2 ， 5)$ ，则一定经过点 $(4 ， 5)$ D、当 $x > 1$ 时， $y$ 随 $x$ 的增大而增大

查看试题解析

二、填空题

11. 二次函数 $y = (m - 1) x^{2}$ 的图象开口向下，则m ．

查看试题解析
12. 如图，AC是圆内接四边形ABCD的一条对角线，点D关于AC的对称点E在边BC上，连接AE.若∠ABC＝64°，则∠BAE的度数为.

查看试题解析
13. 蜜蜂被认为是自然界中最杰出的建筑师，单个蜂巢可以近似地看作是一个正六边形．如图，正六边形的半径 $O A$ 是2，则这个正六边形的边心距 $O H$ 为．

查看试题解析
14. 如图， $M N$ 为⊙O的直径， $A 、 B$ 是⊙O上的两点，过A作 $A C ⊥ M N$ 于点C，过B作 $B D ⊥ M N$ 于点D，P为 $D C$ 上的任意一点，若 $M N = 10$ ， $A C = 4$ ， $B D = 3$ ，则 $P A + P B$ 的最小值是．

查看试题解析
15. 如图，一人口的弧形台阶，从上往下看是一组同心圆被一条直线所截得的一组圆弧.已知每个台阶宽度为32cm（即相邻两弧半径相差32cm），测得AB=200cm，AC=BD=40cm，则弧AB所在的圆的半径为cm

查看试题解析
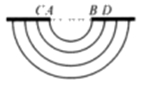16. 已知二次函数 $y = - x^{2} + x + 6$ 及一次函数 $y = - x + m$ ，将该二次函数在x轴上方的图象沿x轴翻折到x轴下方，图象的其余部分不变，得到一个新函数 $($ 如图所示 $)$ ，当直线 $y = - x + m$ 与新图象有4个交点时，m的取值范围是

查看试题解析

三、解答题

17. 若抛物线y＝ax²+bx+c（a≠0）与直线y＝mx+n（m≠0）交y轴于同一点，且抛物线的顶点在直线y＝mx+n上，称该抛物线与直线互为“伙伴函数”．

(1)、求抛物线y＝x²﹣4x+5的“伙伴函数”表达式；

(2)、若直线y＝mx﹣3与抛物线y＝x²﹣6x+c互为“伙伴函数”，求m与c的值；

查看试题解析
18. 手机微信中的抢红包游戏有一种玩法为“拼手气红包”：用户设定好总金额以及红包个数之后，可以生成不等金额的红包，现有四个人组成的微信群中，其中一人发了三个“拼手气红包"，其他三人随机抢红包.

(1)、若甲的速度最快，求甲抢到最多金额的红包的概率.

(2)、若三个人同时点击红包，记金额最多、居中、最少的红包分别为 $A$ 、 $B$ 、 $C$ ，试求出甲抢到红包 $A$ 的概率 $P_{(A)}$ .

查看试题解析
19. 在直径为1000毫米的圆柱形油罐内装进一些油.其横截面如图.油面宽AB=600毫米.

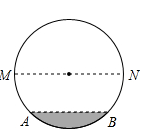(1)、求油的最大深度；

(2)、如果再注入一些油后，油面宽变为800毫米，此时油面上升了多少毫米？

查看试题解析
20. 某商家销售一款商品，该商品的进价为每件80元，现在的售价为每件145元，每天可销售40件商场规定每销售一件需支付给商场管理费5元，通过市场调查发现，该商品单价每降1元，每天销售量增加2件若每件商品降价x元，每天的利润为y元，请完成以下问题的解答．

(1)、用含x的式子表示：①每件商品的售价为元；②每天的销售量为件；

(2)、求出 $y$ 与 $x$ 之间的函数关系式，并求出售价为多少时利润最大？最大利润是多少元？

查看试题解析
21. 已知抛物线 $y = \frac{1}{2} x^{2} + b x + c$ 的对称轴为直线 $x = 1$ ，图象与 $x$ 轴交于点 $(4 ， 0)$ .

(1)、求抛物线的函数表达式；

(2)、若 $(5 ， y_{1})$ 和 $(m ， y_{2})$ 为抛物线上不同的两点，当 $y_{2} > y_{1}$ 时，求出 $m$ 的取值范围；

(3)、若把抛物线的图象沿 $x$ 轴平移 $n$ 个单位，在自变量 $x$ 的值满足 $2 \leq x \leq 3$ 的情况下，与其对应的函数值 $y$ 的最小值为-3，求 $n$ 的值.

查看试题解析
22. 如图，将小旗ACDB放于平面直角坐标系中，得到各顶点的坐标为A（﹣6，12），B（﹣6，0），C（0，6），D（﹣6，6）．以点B为旋转中心，在平面直角坐标系内将小旗顺时针旋转90°．

(1)、画出旋转后的小旗A′C′D′B′；

(2)、写出点A′，C′，D′的坐标；

(3)、求出线段BA旋转到B′A′时所扫过的扇形的面积．

查看试题解析
23. 如图，已知抛物线 $y = x^{2} + b x + c$ 的对称轴为直线 $x = - 1$ ，抛物线与x轴相交于A ， B两点，点A在点B的左侧，点 $C (0 ， - 3)$ 为抛物线与y轴的交点．

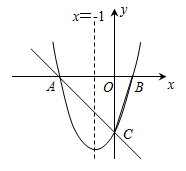(1)、求b和c的值．

(2)、在抛物线的对称轴上存在一点P ，使 $P B + P C$ 最短，请求出点P的坐标．

(3)、抛物线上是否存在一点Q ，使 $△ Q O A$ 的面积等于 $△ B O C$ 的面积的4倍？若存在，求出点Q所有的坐标；若不存在，请说明理由．

查看试题解析
24. 已知，二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象与x轴相交于点A，B（点A在点B的左侧），与y轴相交于点C.

(1)、若 $a = - 1$ ，如图1，已知A，C两点的坐标为 $A (- 1 ， 0) ， C (0 ， 3)$ .
①求抛物线的解析式，并求出B的坐标.

②点P是抛物线上第一象限内一个动点.y轴上有一点 $D (0 ， 1)$ ，连结 $D P$ 交 $B C$ 于点H，若H恰好平分 $D P$ ，求点P的坐标.

(2)、若 $a = 1$ ， $b = k - 1$ ， $c = - k$ ， $k > 0$ ，如图2，抛物线与一次函数 $y = k x + 1$ 的图象交于E，F两点，点E在点F的左侧.在直线 $E F$ 上是否存在唯一一点Q，使得 $∠ A Q O = 90 °$ ？若存在，请求出此时k的值；若不存在，请说明理由.

查看试题解析