2021年秋季浙教版数学九年级上学期期中测试模拟卷(适合杭州地区)
试卷更新日期:2021-10-25 类型:期中考试
一、单选题
-
1. 已知点C在线段AB的延长线上,5CB=2AC,则AB:AC=( )A、 B、 C、 D、2. 如图, , , 为圆上的三点, , 点可能是圆心的是( )A、
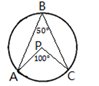 B、
B、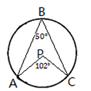 C、
C、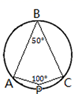 D、
D、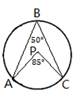 3. 有一个质地均匀且可以转动的转盘,盘面被分成6个全等的扇形区域,在转盘的适当地方涂上灰色,未涂色部分为白色,用力转动转盘,为了使转盘停止时,指针指向灰色的可能性的大小是 ,那么下列涂色方案正确的是( )
3. 有一个质地均匀且可以转动的转盘,盘面被分成6个全等的扇形区域,在转盘的适当地方涂上灰色,未涂色部分为白色,用力转动转盘,为了使转盘停止时,指针指向灰色的可能性的大小是 ,那么下列涂色方案正确的是( )
A、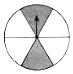 B、
B、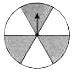 C、
C、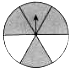 D、
D、 4. 平面直角坐标系中有两条抛物线 与 ,其中 .下列三个结论中:
4. 平面直角坐标系中有两条抛物线 与 ,其中 .下列三个结论中:①如果抛物线 与x轴的一个交点为 ,那么 是抛物线 与x轴的一个交点;
②如果当 时 随x的增大而增大,那么当 时 也随x的增大而增大;
③如果 ,那么x的取值范围为 .
其中正确结论是( )
A、①② B、①③ C、②③ D、①②③5. 在平面直角坐标系 中,⊙O的半径为2,点A(1, )与⊙O的位置关系是( )A、在⊙O上 B、在⊙O内 C、在⊙O外 D、不能确定6. 如图,把 绕着点 顺时针方向旋转 ,得到△ ,点 刚好落在边 上.则 =( ) A、 B、 C、 D、7. 一条弧所对的圆心角为135°,弧长等于半径为3cm的圆的周长的5倍,则这条弧的半径为( )A、45cm B、40cm C、35cm D、30cm8. 如图,已知抛物线 的对称轴在 轴右侧,抛物线与 轴交于点 和点 ,与 轴的负半轴交于点 ,且 ,则下列结论:① ;② ;③ ;④当 时,在 轴下方的抛物线上一定存在关于对称轴对称的两点 , (点 在点 左边),使得 .其中正确的有( )
A、 B、 C、 D、7. 一条弧所对的圆心角为135°,弧长等于半径为3cm的圆的周长的5倍,则这条弧的半径为( )A、45cm B、40cm C、35cm D、30cm8. 如图,已知抛物线 的对称轴在 轴右侧,抛物线与 轴交于点 和点 ,与 轴的负半轴交于点 ,且 ,则下列结论:① ;② ;③ ;④当 时,在 轴下方的抛物线上一定存在关于对称轴对称的两点 , (点 在点 左边),使得 .其中正确的有( )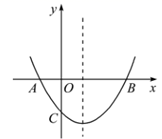 A、1个 B、2个 C、3个 D、4个9. 如图,⊙O的直径AB=8,P是圆上任一点(A,B除外),∠APB的平分线交⊙O于C,弦EF过AC,BC的中点M、N,则EF的长是( )
A、1个 B、2个 C、3个 D、4个9. 如图,⊙O的直径AB=8,P是圆上任一点(A,B除外),∠APB的平分线交⊙O于C,弦EF过AC,BC的中点M、N,则EF的长是( )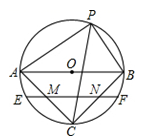 A、 B、 C、6 D、10. 已知二次函数y=ax2﹣2ax﹣3a(a≠0),关于此函数的图象及性质,下列结论中不一定成立的是( )A、该图象的顶点坐标为(1,﹣4a) B、该图象在x轴上截得的线段的长为4 C、若该图象经过点(﹣2,5),则一定经过点(4,5) D、当x>1时,y随x的增大而增大
A、 B、 C、6 D、10. 已知二次函数y=ax2﹣2ax﹣3a(a≠0),关于此函数的图象及性质,下列结论中不一定成立的是( )A、该图象的顶点坐标为(1,﹣4a) B、该图象在x轴上截得的线段的长为4 C、若该图象经过点(﹣2,5),则一定经过点(4,5) D、当x>1时,y随x的增大而增大二、填空题
-
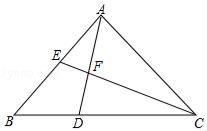
11. 二次函数 的最小值是 .12. 如图,△ABC中,D在BC上,F是AD的中点,连CF并延长交AB于E,已知 ,则 等于 .
 13. 大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”.如图, 为 的黄金分割点 ,如果 的长度为 ,那么 的长度是.
13. 大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”.如图, 为 的黄金分割点 ,如果 的长度为 ,那么 的长度是.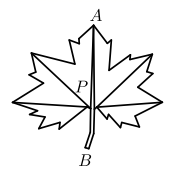 14. 如图,边长为2的等边三角形 , 为 内(包括 的边)一动点,且满足 ,则点 运动的路径的长度为.
14. 如图,边长为2的等边三角形 , 为 内(包括 的边)一动点,且满足 ,则点 运动的路径的长度为.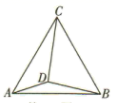 15. 如图,在矩形 中, , .将矩形 绕点 按顺时针方向旋转得到矩形 ,点 落在矩形 的边 上的点 处,连接 ,则 的长是 .
15. 如图,在矩形 中, , .将矩形 绕点 按顺时针方向旋转得到矩形 ,点 落在矩形 的边 上的点 处,连接 ,则 的长是 .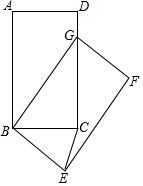 16. 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
16. 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
①4a+b=0;②9a+c>3b;③,3a+c>0;④当x>﹣1时,y的值随x值的增大而增大.⑤ (m为任意实数)其中正确的结论有.(填序号)
三、解答题
-
17. 已知:线段a、b、c,且 = = .(1)、求 的值.(2)、如线段a、b、c满足a+b+c=27.求a、b、c的值.18. 对于抛物线y=x2-4x+3
 (1)、将抛物线的解析式化为顶点式(2)、E坐标系中利用五点法画出此抛物线
(1)、将抛物线的解析式化为顶点式(2)、E坐标系中利用五点法画出此抛物线x
……
……
y
……
……
(3)、指出当x取什么值时,函数的值y随x的增大而增大?19. 将4张分别写有数字1、2、3、4的卡片(卡片的形状、大小、质地都相同)放在盒子中,搅匀后从中任意取出1张卡片,记录后放回、搅匀,再从中任意取出1张卡片.求下列事件发生的概率.(请用“画树状图”或“列表”等方法写出分析过程)(1)、取出的2张卡片数字相同;(2)、取出的2张卡片中,至少有1张卡片的数字为“3”.20. 如图,二次函数 ( 是实数,且 )的图象与 轴交于 、 两点(点 在点 的左侧),其对称轴与 轴交于点 ,已知点 位于第一象限,且在对称轴上, ,点 在 轴的正半轴上, .连接 并延长交 轴于点 ,连接 . (1)、求 、 、 三点的坐标(用数字或含 的式子表示);(2)、已知点 在抛物线的对称轴上,当 的周长的最小值等于 ,求 的值.21. 如图,PM、PN是⊙O的切线,切点分别是A、B,过点O的直线CE∥PN,交⊙O于点C、D,交PM于点E,AD的延长线交PN于点F,若BC∥PM.
(1)、求 、 、 三点的坐标(用数字或含 的式子表示);(2)、已知点 在抛物线的对称轴上,当 的周长的最小值等于 ,求 的值.21. 如图,PM、PN是⊙O的切线,切点分别是A、B,过点O的直线CE∥PN,交⊙O于点C、D,交PM于点E,AD的延长线交PN于点F,若BC∥PM.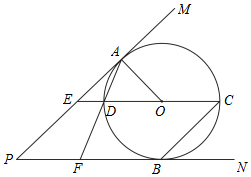 (1)、求证:∠P=45°;(2)、若CD=6,求PF的长.
(1)、求证:∠P=45°;(2)、若CD=6,求PF的长.
